
Small retrosnub icosicosidodecahedron
Encyclopedia
In geometry
, the small retrosnub icosicosidodecahedron is a nonconvex uniform polyhedron
, indexed as U72.
is a nonuniform truncated dodecahedron
.
where τ = (1+√5)/2 is the golden ratio
(sometimes written φ).
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, the small retrosnub icosicosidodecahedron is a nonconvex uniform polyhedron
Nonconvex uniform polyhedron
In geometry, a uniform star polyhedron is a self-intersecting uniform polyhedron. They are also sometimes called nonconvex polyhedra to imply self-intersecting...
, indexed as U72.
Convex hull
Its convex hullConvex hull
In mathematics, the convex hull or convex envelope for a set of points X in a real vector space V is the minimal convex set containing X....
is a nonuniform truncated dodecahedron
Truncated dodecahedron
In geometry, the truncated dodecahedron is an Archimedean solid. It has 12 regular decagonal faces, 20 regular triangular faces, 60 vertices and 90 edges.- Geometric relations :...
.
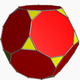 truncated dodecahedron |
 Convex hull |
 Small retrosnub icosicosidodecahedron |
Cartesian coordinates
Cartesian coordinates for the vertices of a small retrosnub icosicosidodecahedron are all the even permutations of- (±½(−1/τ−√(3τ−2)), 0, ±½(3−τ√(3τ−2)))
- (±½(1/τ−√(3τ−2)), ±1, ±½(1+2/τ−τ√(3τ−2)))
- (±½(τ2−√(3τ−2)), ±1/τ, ±½(1−τ√(3τ−2)))
where τ = (1+√5)/2 is the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
(sometimes written φ).

