Schwartz space
Encyclopedia
In mathematics
, Schwartz space is the function space
of functions all of whose derivatives are rapidly decreasing. This space has the important property that the Fourier transform
is an automorphism
on this space. This property enables one, by duality, to define the Fourier transform for elements in the dual space of , that is, for tempered distributions. Schwartz space is named in honour of Laurent Schwartz
, that is, for tempered distributions. Schwartz space is named in honour of Laurent Schwartz
. A function in the Schwartz space is sometimes called a Schwartz function.
 on Rn is the function space
on Rn is the function space
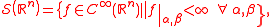
where α, β are multi-indices, C∞(Rn) is the set of smooth functions from Rn to C, and
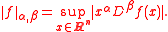
Here, sup denotes the supremum
, and we again use multi-index notation
. When the dimension n is clear, it is convenient to write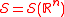 .
.
To put common language to this definition, we could note that a rapidly decreasing function is essentially a function f(x) such that f(x), f'(x), f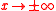 faster than any inverse power of x. Especially,
faster than any inverse power of x. Especially, 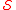 is a subspace of the function space
is a subspace of the function space
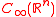 of continuous functions which vanish at infinity.
of continuous functions which vanish at infinity.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, Schwartz space is the function space
Function space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
of functions all of whose derivatives are rapidly decreasing. This space has the important property that the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
is an automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
on this space. This property enables one, by duality, to define the Fourier transform for elements in the dual space of
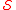 , that is, for tempered distributions. Schwartz space is named in honour of Laurent Schwartz
, that is, for tempered distributions. Schwartz space is named in honour of Laurent SchwartzLaurent Schwartz
Laurent-Moïse Schwartz was a French mathematician. He pioneered the theory of distributions, which gives a well-defined meaning to objects such as the Dirac delta function. He was awarded the Fields medal in 1950 for his work...
. A function in the Schwartz space is sometimes called a Schwartz function.

Definition
The Schwartz space or space of rapidly decreasing functions on Rn is the function space
on Rn is the function space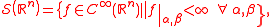
where α, β are multi-indices, C∞(Rn) is the set of smooth functions from Rn to C, and
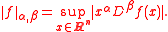
Here, sup denotes the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
, and we again use multi-index notation
Multi-index notation
The mathematical notation of multi-indices simplifies formulae used in multivariable calculus, partial differential equations and the theory of distributions, by generalising the concept of an integer index to an ordered tuple of indices....
. When the dimension n is clear, it is convenient to write
 .
.To put common language to this definition, we could note that a rapidly decreasing function is essentially a function f(x) such that f(x), f'(x), f
 faster than any inverse power of x. Especially,
faster than any inverse power of x. Especially, 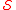 is a subspace of the function space
is a subspace of the function spaceFunction space
In mathematics, a function space is a set of functions of a given kind from a set X to a set Y. It is called a space because in many applications it is a topological space, a vector space, or both.-Examples:...
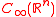 of continuous functions which vanish at infinity.
of continuous functions which vanish at infinity.Examples of functions in S
- If i is a multi-index, and a is a positive real number, then
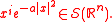
- Any smooth function f with compact support is in
 . This is clear since any derivative of f is continuous and supported in the support of f, so (xα Dβ) f has a maximum in Rn by the extreme value theoremExtreme value theoremIn calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
. This is clear since any derivative of f is continuous and supported in the support of f, so (xα Dβ) f has a maximum in Rn by the extreme value theoremExtreme value theoremIn calculus, the extreme value theorem states that if a real-valued function f is continuous in the closed and bounded interval [a,b], then f must attain its maximum and minimum value, each at least once...
.
Properties
-
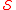 is a Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
is a Fréchet spaceFréchet spaceIn functional analysis and related areas of mathematics, Fréchet spaces, named after Maurice Fréchet, are special topological vector spaces. They are generalizations of Banach spaces...
over the complex numbers.
- Using Leibniz' rule, it follows that
 is also closed under point-wise multiplication; if
is also closed under point-wise multiplication; if  , then
, then 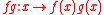 is also in
is also in  .
.
- For any 1 ≤ p ≤ ∞, we have
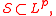 where Lp(Rn) is the space of p-integrable functionsLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
where Lp(Rn) is the space of p-integrable functionsLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
on Rn.
- The space of all bump functions,
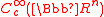 , is included in
, is included in 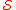 .
.
- The Fourier transform is a linear isomorphism
 .
.
- If
 then
then 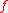 is uniformly continuous on
is uniformly continuous on  .
.

