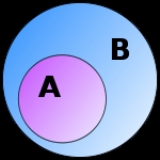
Inclusion map
Encyclopedia

Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, if
 is a subset
is a subsetSubset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of
 , then the inclusion map (also inclusion function, or canonical injection) is the function
, then the inclusion map (also inclusion function, or canonical injection) is the functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
 that sends each element,
that sends each element,  of
of  to
to  , treated as an element of
, treated as an element of  :
:
A "hooked arrow"
 is sometimes used in place of the function arrow above to denote an inclusion map.
is sometimes used in place of the function arrow above to denote an inclusion map.This and other analogous injective functions from substructure
Substructure
In mathematical logic, an substructure or subalgebra is a structure whose domain is a subset of that of a bigger structure, and whose functions and relations are the traces of the functions and relations of the bigger structure...
s are sometimes called natural injections.
Given any morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
between objects X and Y, if there is an inclusion map into the domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
 , then one can form the restriction fi of f. In many instances, one can also construct a canonical inclusion into the codomain
, then one can form the restriction fi of f. In many instances, one can also construct a canonical inclusion into the codomainCodomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
R→Y known as the range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
of f.
Applications of inclusion maps
Inclusion maps tend to be homomorphismHomomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s of algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
s; thus, such inclusion maps are embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
s. More precisely, given a sub-structure closed under some operations, the inclusion map will be an embedding for tautological reasons, given the very definition by restriction of what one checks. For example, for a binary operation
 , to require that
, to require that
is simply to say that
 is consistently computed in the sub-structure and the large structure. The case of a unary operation
is consistently computed in the sub-structure and the large structure. The case of a unary operationUnary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
is similar; but one should also look at nullary operations, which pick out a constant element. Here the point is that closure
Closure (mathematics)
In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...
means such constants must already be given in the substructure.
Inclusion maps are seen in algebraic topology where if A is a strong deformation retract of X, the inclusion map yields an isomorphism between all homotopy groups (i.e. is a homotopy equivalence
Homotopy
In topology, two continuous functions from one topological space to another are called homotopic if one can be "continuously deformed" into the other, such a deformation being called a homotopy between the two functions...
)
Inclusion maps in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
come in different kinds: for example embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
s of submanifold
Submanifold
In mathematics, a submanifold of a manifold M is a subset S which itself has the structure of a manifold, and for which the inclusion map S → M satisfies certain properties. There are different types of submanifolds depending on exactly which properties are required...
s. Contravariant objects such as differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s restrict to submanifolds, giving a mapping in the other direction. Another example, more sophisticated, is that of affine schemes, for which the inclusions
- Spec(R/I) → Spec(R)
and
- Spec(R/I2) → Spec(R)
may be different morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
s, where R is a commutative ring
Commutative ring
In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
and I an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
.

