Pseudometric space
Encyclopedia
In mathematics
, a pseudometric space is a generalized metric space
in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space
, every seminormed space is a pseudometric space. Because of this analogy the term semimetric space (which has a different meaning in topology
) is sometimes used as a synonym, especially in functional analysis
.
When a topology is generated using a family of pseudometrics, the space is called a gauge space.
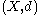is a set 
together with a non-negative real-valued function 
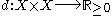(called a pseudometric) such that, for every 
,
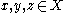Unlike a metric space, points in a pseudometric space need not be distinguishable
; that is, one may have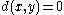
for distinct values 
.
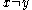. Consider the space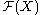
of real-valued functions 
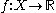together with a special point 
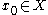. This point then induces a pseudometric on the space of functions, given by
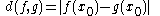
for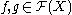
For vector spaces V, a seminorm p induces a pseudometric on V, as
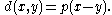
Conversely, a homogeneous, translation invariant pseudometric induces a seminorm.
induced by the open balls
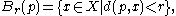
which form a basis for the topology. A topological space is said to be a pseudometrizable topological space if the space can be given a pseudometric such that the pseudometric topology coincides with the given topology on the space.
The difference between pseudometrics and metrics is entirely topological. That is, a pseudometric is a metric if and only if the topology it generates is T0 (i.e. distinct points are topologically distinguishable).
, called the metric identification, that converts the pseudometric space into a full-fledged metric space
. This is done by defining
if 
. Let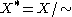 
and let
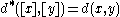
Then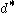
is a metric on 
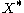and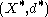 
is a well-defined metric space.
The metric identification preserves the induced topologies. That is, a subset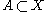
is open (or closed) in 
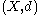if and only if 
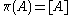is open (or closed) in 
.
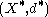Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pseudometric space is a generalized metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
in which the distance between two distinct points can be zero. In the same way as every normed space is a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, every seminormed space is a pseudometric space. Because of this analogy the term semimetric space (which has a different meaning in topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
) is sometimes used as a synonym, especially in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.
When a topology is generated using a family of pseudometrics, the space is called a gauge space.
Definition
A pseudometric space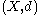 is a set together with a non-negative real-valued function 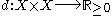(called a pseudometric) such that, for every ,
.
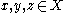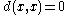(symmetry)
(subadditivity/triangle inequalityTriangle inequalityIn mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
)
Unlike a metric space, points in a pseudometric space need not be distinguishable
Identity of indiscernibles
The identity of indiscernibles is an ontological principle which states that two or more objects or entities are identical if they have all their properties in common. That is, entities x and y are identical if any predicate possessed by x is also possessed by y and vice versa...
; that is, one may have
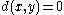for distinct values 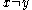.Examples
Pseudometrics arise naturally in functional analysisFunctional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
. Consider the space
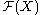of real-valued functions 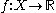together with a special point 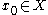. This point then induces a pseudometric on the space of functions, given by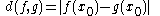for
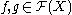
For vector spaces V, a seminorm p induces a pseudometric on V, as
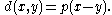
Conversely, a homogeneous, translation invariant pseudometric induces a seminorm.
Topology
The pseudometric topology is the topologyTopological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
induced by the open balls
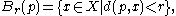
which form a basis for the topology. A topological space is said to be a pseudometrizable topological space if the space can be given a pseudometric such that the pseudometric topology coincides with the given topology on the space.
The difference between pseudometrics and metrics is entirely topological. That is, a pseudometric is a metric if and only if the topology it generates is T0 (i.e. distinct points are topologically distinguishable).
Metric identification
The vanishing of the pseudometric induces an equivalence relationEquivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, called the metric identification, that converts the pseudometric space into a full-fledged metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. This is done by defining
if . Let 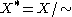and let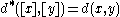Then
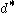is a metric on 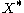and 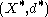is a well-defined metric space.The metric identification preserves the induced topologies. That is, a subset
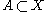is open (or closed) in 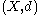if and only if 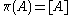is open (or closed) in .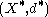