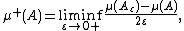
Isoperimetry
Encyclopedia
The isoperimetric inequality is a geometric
inequality involving the square of the circumference
of a closed curve in the plane and the area
of a plane region it encloses, as well as its various generalizations. Isoperimetric literally means "having the same perimeter
". Specifically, the isoperimetric inequality states, for the length L of a closed curve and the area A of the planar region that it encloses, that
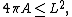
and that equality holds if and only if the curve is a circle.
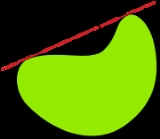
The isoperimetric problem is to determine a plane figure of the largest possible area whose boundary
has a specified length
. The closely related Dido's problem asks for a region of the maximal area bounded by a straight line and a curvilinear arc
whose endpoints belong to that line. It is named after Dido, the legendary founder and first queen of Carthage
. The solution to the isoperimetric problem is given by a circle
and was known already in Ancient Greece
. However, the first mathematically rigorous proof of this fact was obtained only in the 19th century. Since then, many other proofs have been found, some of them stunningly simple. The isoperimetric problem has been extended in multiple ways, for example, to curves on surfaces
and to regions in higher-dimensional spaces.
Perhaps the most familiar physical manifestation of the 3-dimensional isoperimetric inequality is the shape of a drop of water. Namely, a drop will typically assume a symmetric round shape. Since the amount of water in a drop is fixed, surface tension
forces the drop into a shape which minimizes the surface area of the drop, namely a round sphere.
The classical isoperimetric problem dates back to antiquity. The problem can be stated as follows: Among all closed curve
s in the plane of fixed perimeter, which curve (if any) maximizes the area of its enclosed region? This question can be shown to be equivalent to the following problem: Among all closed curves in the plane enclosing a fixed area, which curve (if any) minimizes the perimeter?
This problem is conceptually related to the principle of least action
in physics
, in that it can be restated: what is the principle of action which encloses the greatest area, with the greatest economy of effort? The 15th-century philosopher and scientist, Cardinal Nicholas of Cusa
, considered rotation
al action, the process by which a circle
is generated, to be the most direct reflection, in the realm of sensory impressions, of the process by which the universe is created. German astronomer and astrologer Johannes Kepler
invoked the isoperimetric principle in discussing the morphology of the solar system, in Mysterium Cosmographicum
(The Sacred Mystery of the Cosmos, 1596).
Although the circle appears to be an obvious solution to the problem, proving this fact is rather difficult. The first progress toward the solution was made by Swiss geometer Jakob Steiner
in 1838, using a geometric method later named Steiner symmetrisation. Steiner showed that if a solution existed, then it must be the circle. Steiner's proof was completed later by several other mathematician
s.
Steiner begins with some geometric constructions which are easily understood; for example, it can be shown that any closed curve enclosing a region that is not fully convex
can be modified to enclose more area, by "flipping" the concave areas so that they become convex. It can further be shown that any closed curve which is not fully symmetrical can be "tilted" so that it encloses more area. The one shape that is perfectly convex and symmetrical is the circle, although this, in itself, does not represent a rigorous proof of the isoperimetric theorem (see external links).
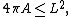
and that the equality holds if and only if the curve is a circle.
Indeed, the area of a disk of radius R is πR2 and the circumference of the circle is 2πR, so both sides of the inequality are equal to 4π2R2 in this case.
Dozens of proofs of the isoperimetric inequality have been found. In 1902, Hurwitz
published a short proof using the Fourier series
that applies to arbitrary rectifiable curves (not assumed to be smooth). An elegant direct proof based on comparison of a smooth simple closed curve with an appropriate circle was given by E. Schmidt in 1938. It uses only the arc length
formula, expression for the area of a plane region from Green's theorem
, and the Cauchy–Schwarz inequality
.
For a given closed curve, the isoperimetric quotient is defined as the ratio of its area and that of the circle having the same perimeter. This is equal to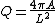
and the isoperimetric inequality says that Q ≤ 1.
The isoperimetric quotient of a regular n-gon is
.
of radius 1. Denote by L the length of C and by A the area enclosed by C. The spherical isoperimetric inequality states that
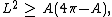
and that the equality holds if and only if the curve is a circle. There are, in fact, two ways to measure the spherical area enclosed by a simple closed curve, but the inequality is symmetric with the respect to taking the complement.
This inequality was discovered by Paul Lévy
(1919) who also extended it to higher dimensions and general surfaces.
. Among all simple closed surfaces with given surface area
, the sphere
encloses a region of maximal volume
. An analogous statement holds in Euclidean spaces of any dimension.
In full generality , the isoperimetric inequality states that for any set S ⊂ Rn whose closure has finite Lebesgue measure
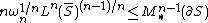
where M*n-1 is the (n-1)-dimensional Minkowski content
, Ln is the n-dimensional Lebesgue measure, and ωn is the volume of the unit ball in Rn. If the boundary of S is rectifiable, then the Minkowski content is the (n-1)-dimensional Hausdorff measure
.
The isoperimetric inequality in n-dimensions can be quickly proven by the Brunn-Minkowski inequality .
The n-dimensional isoperimetric inequality is equivalent (for sufficiently smooth domains) to the Sobolev inequality
on Rn with optimal constant: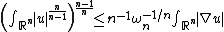
for all u ∈ W1,1(Rn).
s, or more generally, in Riemannian manifold
s. However, the isoperimetric problem can be formulated in much greater generality, using the notion of Minkowski content. Let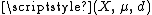
be a metric measure space: X is a metric space
with metric
d, and μ is a Borel measure on X. The boundary measure, or Minkowski content
, of a measurable subset A of X is defined as the lim inf
where
is the ε-extension of A.
The isoperimetric problem in X asks how small can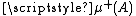
be for a given μ(A). If X is the Euclidean plane
with the usual distance
and the Lebesgue measure
then this question generalizes the classical isoperimetric problem to planar regions whose boundary is not necessarily smooth, although the answer turns out to be the same.
The function
is called the isoperimetric profile of the metric measure space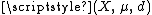
. Isoperimetric profiles have been studied for Cayley graph
s of discrete group
s and for special classes of Riemannian manifolds (where usually only regions A with regular boundary are considered).
, isoperimetric inequalities are at the heart of the study of expander graphs, which are sparse graphs that have strong connectivity properties. Expander constructions have spawned research in pure and applied mathematics, with several applications to complexity theory
, design of robust computer network
s, and the theory of error-correcting codes.
Isoperimetric inequalities for graphs relate the size of vertex subsets to the size of their boundary, which is usually measured by the number of edges leaving the subset (edge expansion) or by the number of neighbouring vertices (vertex expansion). For a graph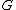
and a number 
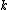, the following are two standard isoperimetric parameters for graphs.
Here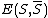
denotes the set of edges leaving 
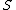and 
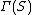denotes the set of vertices that have a neighbour in 
.
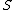The isoperimetric problem consists of understanding how the parameters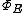
and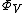 
behave for natural families of graphs.
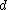-dimensional hypercube
is the graph whose vertices are all Boolean vectors of length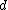 
, that is, the set 
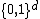. Two such vectors are connected by an edge in 
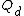if they are equal up to a single bit flip, that is, their Hamming distance
is exactly one.
The following are the isoperimetric inequalities for the Boolean hypercube.
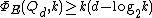. This bound is tight, as is witnessed by each set 
that is the set of vertices of any subcube of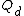 
.
at most
and no points of Hamming weight larger than 
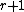for some integer 
.
This theorem implies that any set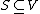
with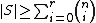 
satisfies 
.
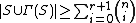As a special case, consider set sizes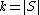
of the form 
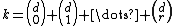for some integer 
. Then the above implies that the exact vertex isoperimetric parameter is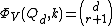 
.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
inequality involving the square of the circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
of a closed curve in the plane and the area
Area
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
of a plane region it encloses, as well as its various generalizations. Isoperimetric literally means "having the same perimeter
Perimeter
A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...
". Specifically, the isoperimetric inequality states, for the length L of a closed curve and the area A of the planar region that it encloses, that
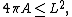
and that equality holds if and only if the curve is a circle.
The isoperimetric problem is to determine a plane figure of the largest possible area whose boundary
Boundary (topology)
In topology and mathematics in general, the boundary of a subset S of a topological space X is the set of points which can be approached both from S and from the outside of S. More precisely, it is the set of points in the closure of S, not belonging to the interior of S. An element of the boundary...
has a specified length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
. The closely related Dido's problem asks for a region of the maximal area bounded by a straight line and a curvilinear arc
Arc (geometry)
In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
whose endpoints belong to that line. It is named after Dido, the legendary founder and first queen of Carthage
Carthage
Carthage , implying it was a 'new Tyre') is a major urban centre that has existed for nearly 3,000 years on the Gulf of Tunis, developing from a Phoenician colony of the 1st millennium BC...
. The solution to the isoperimetric problem is given by a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
and was known already in Ancient Greece
Ancient Greece
Ancient Greece is a civilization belonging to a period of Greek history that lasted from the Archaic period of the 8th to 6th centuries BC to the end of antiquity. Immediately following this period was the beginning of the Early Middle Ages and the Byzantine era. Included in Ancient Greece is the...
. However, the first mathematically rigorous proof of this fact was obtained only in the 19th century. Since then, many other proofs have been found, some of them stunningly simple. The isoperimetric problem has been extended in multiple ways, for example, to curves on surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
and to regions in higher-dimensional spaces.
Perhaps the most familiar physical manifestation of the 3-dimensional isoperimetric inequality is the shape of a drop of water. Namely, a drop will typically assume a symmetric round shape. Since the amount of water in a drop is fixed, surface tension
Surface tension
Surface tension is a property of the surface of a liquid that allows it to resist an external force. It is revealed, for example, in floating of some objects on the surface of water, even though they are denser than water, and in the ability of some insects to run on the water surface...
forces the drop into a shape which minimizes the surface area of the drop, namely a round sphere.
The isoperimetric problem in the plane
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s in the plane of fixed perimeter, which curve (if any) maximizes the area of its enclosed region? This question can be shown to be equivalent to the following problem: Among all closed curves in the plane enclosing a fixed area, which curve (if any) minimizes the perimeter?
This problem is conceptually related to the principle of least action
Principle of least action
In physics, the principle of least action – or, more accurately, the principle of stationary action – is a variational principle that, when applied to the action of a mechanical system, can be used to obtain the equations of motion for that system...
in physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, in that it can be restated: what is the principle of action which encloses the greatest area, with the greatest economy of effort? The 15th-century philosopher and scientist, Cardinal Nicholas of Cusa
Nicholas of Cusa
Nicholas of Kues , also referred to as Nicolaus Cusanus and Nicholas of Cusa, was a cardinal of the Catholic Church from Germany , a philosopher, theologian, jurist, mathematician, and an astronomer. He is widely considered one of the great geniuses and polymaths of the 15th century...
, considered rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
al action, the process by which a circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is generated, to be the most direct reflection, in the realm of sensory impressions, of the process by which the universe is created. German astronomer and astrologer Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
invoked the isoperimetric principle in discussing the morphology of the solar system, in Mysterium Cosmographicum
Mysterium Cosmographicum
Mysterium Cosmographicum, is an astronomy book by the German astronomer Johannes Kepler, published at Tübingen in 1596 and in a second edition in 1621...
(The Sacred Mystery of the Cosmos, 1596).
Although the circle appears to be an obvious solution to the problem, proving this fact is rather difficult. The first progress toward the solution was made by Swiss geometer Jakob Steiner
Jakob Steiner
Jakob Steiner was a Swiss mathematician who worked primarily in geometry.-Personal and professional life:...
in 1838, using a geometric method later named Steiner symmetrisation. Steiner showed that if a solution existed, then it must be the circle. Steiner's proof was completed later by several other mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s.
Steiner begins with some geometric constructions which are easily understood; for example, it can be shown that any closed curve enclosing a region that is not fully convex
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
can be modified to enclose more area, by "flipping" the concave areas so that they become convex. It can further be shown that any closed curve which is not fully symmetrical can be "tilted" so that it encloses more area. The one shape that is perfectly convex and symmetrical is the circle, although this, in itself, does not represent a rigorous proof of the isoperimetric theorem (see external links).
The isoperimetric inequality
The solution to the isoperimetric problem is usually expressed in the form of an inequality that relates the length L of a closed curve and the area A of the planar region that it encloses. The isoperimetric inequality states that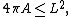and that the equality holds if and only if the curve is a circle.
Indeed, the area of a disk of radius R is πR2 and the circumference of the circle is 2πR, so both sides of the inequality are equal to 4π2R2 in this case.
Dozens of proofs of the isoperimetric inequality have been found. In 1902, Hurwitz
Adolf Hurwitz
Adolf Hurwitz was a German mathematician.-Early life:He was born to a Jewish family in Hildesheim, former Kingdom of Hannover, now Lower Saxony, Germany, and died in Zürich, in Switzerland. Family records indicate that he had siblings and cousins, but their names have yet to be confirmed...
published a short proof using the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
that applies to arbitrary rectifiable curves (not assumed to be smooth). An elegant direct proof based on comparison of a smooth simple closed curve with an appropriate circle was given by E. Schmidt in 1938. It uses only the arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
formula, expression for the area of a plane region from Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
, and the Cauchy–Schwarz inequality
Cauchy–Schwarz inequality
In mathematics, the Cauchy–Schwarz inequality , is a useful inequality encountered in many different settings, such as linear algebra, analysis, probability theory, and other areas...
.
For a given closed curve, the isoperimetric quotient is defined as the ratio of its area and that of the circle having the same perimeter. This is equal to
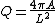
and the isoperimetric inequality says that Q ≤ 1.
The isoperimetric quotient of a regular n-gon is
.The isoperimetric inequality on the sphere
Let C be a simple closed curve on a sphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
of radius 1. Denote by L the length of C and by A the area enclosed by C. The spherical isoperimetric inequality states that
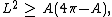
and that the equality holds if and only if the curve is a circle. There are, in fact, two ways to measure the spherical area enclosed by a simple closed curve, but the inequality is symmetric with the respect to taking the complement.
This inequality was discovered by Paul Lévy
Paul Pierre Lévy
Paul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...
(1919) who also extended it to higher dimensions and general surfaces.
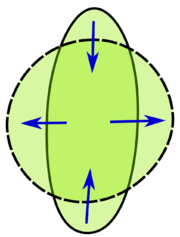
Isoperimetric inequality in higher dimensions
The isoperimetric theorem generalizes to surfaces in the three-dimensional Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. Among all simple closed surfaces with given surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
, the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
encloses a region of maximal volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
. An analogous statement holds in Euclidean spaces of any dimension.
In full generality , the isoperimetric inequality states that for any set S ⊂ Rn whose closure has finite Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
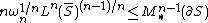
where M*n-1 is the (n-1)-dimensional Minkowski content
Minkowski content
The Minkowski content of a set, or the boundary measure, is a basic concept in geometry and measure theory which generalizes to arbitrary measurable sets the notions of length of a smooth curve in the plane and area of a smooth surface in the space...
, Ln is the n-dimensional Lebesgue measure, and ωn is the volume of the unit ball in Rn. If the boundary of S is rectifiable, then the Minkowski content is the (n-1)-dimensional Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
.
The isoperimetric inequality in n-dimensions can be quickly proven by the Brunn-Minkowski inequality .
The n-dimensional isoperimetric inequality is equivalent (for sufficiently smooth domains) to the Sobolev inequality
Sobolev inequality
In mathematics, there is in mathematical analysis a class of Sobolev inequalities, relating norms including those of Sobolev spaces. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev spaces, and the Rellich–Kondrachov theorem showing that under...
on Rn with optimal constant:
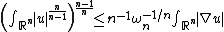
for all u ∈ W1,1(Rn).
Isoperimetric inequalities in a metric measure space
Most of the work on isoperimetric problem has been done in the context of smooth regions in Euclidean spaceEuclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
s, or more generally, in Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
s. However, the isoperimetric problem can be formulated in much greater generality, using the notion of Minkowski content. Let
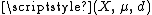be a metric measure space: X is a metric spaceMetric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
with metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
d, and μ is a Borel measure on X. The boundary measure, or Minkowski content
Minkowski content
The Minkowski content of a set, or the boundary measure, is a basic concept in geometry and measure theory which generalizes to arbitrary measurable sets the notions of length of a smooth curve in the plane and area of a smooth surface in the space...
, of a measurable subset A of X is defined as the lim inf
where
is the ε-extension of A.
The isoperimetric problem in X asks how small can
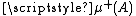be for a given μ(A). If X is the Euclidean planePlane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
with the usual distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
and the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
then this question generalizes the classical isoperimetric problem to planar regions whose boundary is not necessarily smooth, although the answer turns out to be the same.
The function
is called the isoperimetric profile of the metric measure space
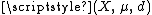. Isoperimetric profiles have been studied for Cayley graphCayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
s of discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
s and for special classes of Riemannian manifolds (where usually only regions A with regular boundary are considered).
Isoperimetric inequalities for Graphs
In graph theoryGraph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, isoperimetric inequalities are at the heart of the study of expander graphs, which are sparse graphs that have strong connectivity properties. Expander constructions have spawned research in pure and applied mathematics, with several applications to complexity theory
Computational complexity theory
Computational complexity theory is a branch of the theory of computation in theoretical computer science and mathematics that focuses on classifying computational problems according to their inherent difficulty, and relating those classes to each other...
, design of robust computer network
Computer network
A computer network, often simply referred to as a network, is a collection of hardware components and computers interconnected by communication channels that allow sharing of resources and information....
s, and the theory of error-correcting codes.
Isoperimetric inequalities for graphs relate the size of vertex subsets to the size of their boundary, which is usually measured by the number of edges leaving the subset (edge expansion) or by the number of neighbouring vertices (vertex expansion). For a graph
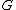and a number 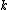, the following are two standard isoperimetric parameters for graphs.
- The edge isoperimetric parameter:
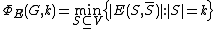
- The vertex isoperimetric parameter:
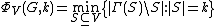
Here
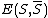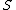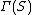denotes the set of edges leaving and denotes the set of vertices that have a neighbour in 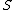.The isoperimetric problem consists of understanding how the parameters
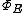and 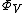behave for natural families of graphs.Example: Isoperimetric inequalities for hypercubes
The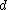-dimensional hypercubeHypercube
In geometry, a hypercube is an n-dimensional analogue of a square and a cube . It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length.An...
is the graph whose vertices are all Boolean vectors of length 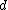, that is, the set 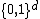. Two such vectors are connected by an edge in 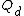if they are equal up to a single bit flip, that is, their Hamming distanceHamming distance
In information theory, the Hamming distance between two strings of equal length is the number of positions at which the corresponding symbols are different...
is exactly one.
The following are the isoperimetric inequalities for the Boolean hypercube.
Edge isoperimetric inequality
The edge isoperimetric inequality of the hypercube is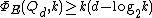. This bound is tight, as is witnessed by each set that is the set of vertices of any subcube of 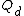.Vertex isoperimetric inequality
Harper's theorem says that Hamming balls have the smallest vertex boundary among all sets of a given size. Hamming balls are sets that contain all points of Hamming weightHamming weight
The Hamming weight of a string is the number of symbols that are different from the zero-symbol of the alphabet used. It is thus equivalent to the Hamming distance from the all-zero string of the same length. For the most typical case, a string of bits, this is the number of 1's in the string...
at most
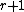and no points of Hamming weight larger than for some integer .This theorem implies that any set
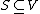with 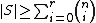satisfies 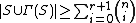.As a special case, consider set sizes
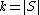of the form 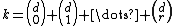for some integer . Then the above implies that the exact vertex isoperimetric parameter is 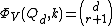.See also
- Isoperimetric dimensionIsoperimetric dimensionIn mathematics, the isoperimetric dimension of a manifold is a notion of dimension that tries to capture how the large-scale behavior of the manifold resembles that of a Euclidean space .In the Euclidean space, the isoperimetric inequality says...
- Chaplygin problemChaplygin problemIn mathematics, particularly in the fields of nonlinear dynamics and the calculus of variations, the Chaplygin problem is an isoperimetric problem with a differential constraint. Specifically, the problem is to determine what flight path an airplane in a constant wind field should take in order to...
- Gaussian isoperimetric inequality
- Lévy–Gromov inequality
- Expander graphExpander graphIn combinatorics, an expander graph is a sparse graph that has strong connectivity properties, quantified using vertex, edge or spectral expansion as described below...
- Planar separator theoremPlanar separator theoremIn graph theory, the planar separator theorem is a form of isoperimetric inequality for planar graphs, that states that any planar graph can be split into smaller pieces by removing a small number of vertices...
External links
- History of the Isoperimetric Problem at Convergence
- Treiberg: Several proofs of the isoperimetric inequality
- Isoperimetric Theorem at cut-the-knotCut-the-knotCut-the-knot is a free, advertisement-funded educational website maintained by Alexander Bogomolny and devoted to popular exposition of many topics in mathematics. The site has won more than 20 awards from scientific and educational publications, including a Scientific American Web Award in 2003,...