Borel measure
Encyclopedia
In mathematics
, specifically in measure theory
, a Borel measure is defined as follows: let X be a locally compact Hausdorff space
, and let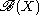
be the smallest σ-algebra that contains the open sets of X; this is known as the σ-algebra of Borel sets. Any measure μ defined on the σ-algebra of Borel sets is called a Borel measure. Some authors require in addition that μ(C) < ∞ for every compact set C. If a Borel measure μ is both inner regular and outer regular, it is called a regular Borel measure. If μ is both inner regular and locally finite
, it is called a Radon measure
. Note that a locally finite Borel measure automatically satisfies μ(C) < ∞ for every compact set C.
is a locally compact Hausdorff space, hence we can define a Borel measure on it. In this case,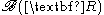
is the smallest σ-algebra that contains the open intervals of R. While there are many Borel measures μ, the choice of Borel measure which assigns 
for every interval 
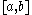is sometimes called "the" Borel measure on R. In practice, even "the" Borel measure is not the most useful measure defined on the σ-algebra of Borel sets; indeed, the Lebesgue measure
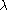is an extension of "the" Borel measure which possesses the crucial property that it is a complete measure
(unlike the Borel measure). To clarify, when one says that the Lebesgue measure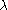
is an extension of the Borel measure 
, it means that every Borel measureable set E is also a Lebesgue measureable set, and the Borel measure and the Lebesgue measure coincide on the Borel sets (i.e.,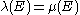 
for every Borel measureable set).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in measure theory
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, a Borel measure is defined as follows: let X be a locally compact Hausdorff space
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
, and let
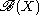be the smallest σ-algebra that contains the open sets of X; this is known as the σ-algebra of Borel sets. Any measure μ defined on the σ-algebra of Borel sets is called a Borel measure. Some authors require in addition that μ(C) < ∞ for every compact set C. If a Borel measure μ is both inner regular and outer regular, it is called a regular Borel measure. If μ is both inner regular and locally finiteLocally finite measure
In mathematics, a locally finite measure is a measure for which every point of the measure space has a neighbourhood of finite measure.-Definition:...
, it is called a Radon measure
Radon measure
In mathematics , a Radon measure, named after Johann Radon, is a measure on the σ-algebra of Borel sets of a Hausdorff topological space X that is locally finite and inner regular.-Motivation:...
. Note that a locally finite Borel measure automatically satisfies μ(C) < ∞ for every compact set C.
On the real line
The real line R with its usual topologyReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
is a locally compact Hausdorff space, hence we can define a Borel measure on it. In this case,
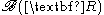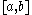is the smallest σ-algebra that contains the open intervals of R. While there are many Borel measures μ, the choice of Borel measure which assigns for every interval is sometimes called "the" Borel measure on R. In practice, even "the" Borel measure is not the most useful measure defined on the σ-algebra of Borel sets; indeed, the Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
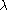is an extension of "the" Borel measure which possesses the crucial property that it is a complete measureComplete measure
In mathematics, a complete measure is a measure space in which every subset of every null set is measurable...
(unlike the Borel measure). To clarify, when one says that the Lebesgue measure
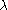is an extension of the Borel measure , it means that every Borel measureable set E is also a Lebesgue measureable set, and the Borel measure and the Lebesgue measure coincide on the Borel sets (i.e., 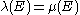for every Borel measureable set).