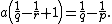Sobolev inequality
Encyclopedia
In mathematics
, there is in mathematical analysis
a class of Sobolev inequalities, relating norms including those of Sobolev space
s. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev space
s, and the Rellich–Kondrachov theorem showing that under slightly stronger conditions some Sobolev spaces are compactly embedded
in others. They are named after Sergei Lvovich Sobolev
.
s are functions in Lp
. Here k is a non-negative integer and 1 ≤ p ≤ ∞. The first part of the Sobolev embedding theorem states that
if k > ℓ and 1 ≤ p < q ≤ ∞ are two extended real numbers such that (k-l)p < n and :
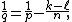
then
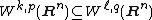
and the embedding is continuous. In the special case of k = 1 and ℓ = 0, Sobolev embedding gives
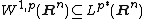
where p∗ is the Sobolev conjugate of p, given by
This special case of the Sobolev embedding is a direct consequence of the Gagliardo–Nirenberg–Sobolev inequality.
The second part of the Sobolev embedding theorem applies to embeddings in Hölder spaces Cr,α(Rn). If (k−r−α)/n = 1/p with α ∈ (0,1), then one has the embedding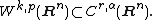
This part of the Sobolev embedding is a direct consequence of Morrey's inequality. Intuitively, this inclusion expresses the fact that the existence of sufficiently many weak derivatives implies some continuity of the classical derivatives.
Generalizations
The Sobolev embedding theorem holds for Sobolev spaces Wk,p(M) on other suitable domains M. In particular , both parts of the Sobolev embedding hold when
Kondrachov embedding theorem
On a compact manifold with C1 boundary, the Kondrachov embedding theorem states that if k> ℓ and k−n/p > ℓ−n/q then the Sobolev embedding
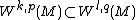
is completely continuous (compact).
where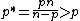
is the Sobolev conjugate of p.
The Gagliardo–Nirenberg–Sobolev inequality implies directly the Sobolev embedding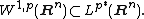
The embeddings in other orders on Rn are then obtained by suitable iteration.
Let 0 < αα = (−Δ)−α/2 be the Riesz potential
on Rn. Then, for q defined by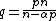
there exists a constant C depending only on p such that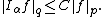
If p = 1, then the weak-type estimate holds: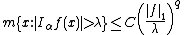
where 1/q = 1 − α/n.
The Hardy–Littlewood–Sobolev lemma implies the Sobolev embedding essentially by the relationship between the Riesz transforms and the Riesz potentials.
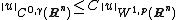
for all u ∈ C1(Rn) ∩ Lp(Rn), where
Thus if u ∈ W1,p(Rn), then u is in fact Hölder continuous of exponent γ,
after possibly being redefined on a set of measure 0.
A similar result holds in a bounded domain U with C1 boundary. In this case,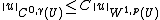
where the constant C depends now on n, p and U. This version of the inequality follows from the previous one by applying the norm-preserving extension of W1,p(U) to W1,p(Rn).
(i) If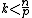
then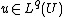
, where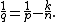
We have in addition the estimate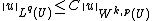
,
the constant C depending only on k, p, n, and U.
(ii) If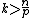
then u belongs to the Hölder space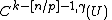
, where
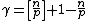if n/p is not an integer, or
We have in addition the estimate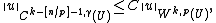
the constant C depending only on k, p, n, γ, and U.
Case
If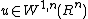 
, then 
is a function of bounded mean oscillation
and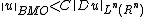
, for some constant C depending only on n.
This estimate is a corollary of the Poincaré inequality
.
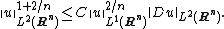
The inequality follows from basic properties of the Fourier transform
. Indeed, integrating over the complement of the ball of radius ρ,
by Parseval's theorem
. On the other hand, one has
which, when integrated over the ball of radius ρ gives
where ωn is the volume of the n-ball. Choosing ρ to minimize the sum of and and again applying Parseval's theorem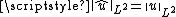
gives the inequality.
In the special case of n =1, the Nash inequality can be extended to the Lp case, in which case it is a generalization of the Gagliardo-Nirenberg-Sobolev inequality . In fact, if I is a bounded interval, then for all 1 ≤ r < ∞ and all 1 ≤ q ≤ p < ∞ the following inequality holds
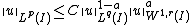
where a is defined by
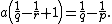
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, there is in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
a class of Sobolev inequalities, relating norms including those of Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s. These are used to prove the Sobolev embedding theorem, giving inclusions between certain Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s, and the Rellich–Kondrachov theorem showing that under slightly stronger conditions some Sobolev spaces are compactly embedded
Compactly embedded
In mathematics, the notion of being compactly embedded expresses the idea that one set or space is "well contained" inside another. There are versions of this concept appropriate to general topology and functional analysis.-Definition :...
in others. They are named after Sergei Lvovich Sobolev
Sergei Lvovich Sobolev
Sergei Lvovich Sobolev was a Soviet mathematician working in mathematical analysis and partial differential equations. He was born in St. Petersburg, and died in Moscow.-Work:...
.
Sobolev embedding theorem
Let Wk,p(Rn) denote the Sobolev space consisting of all real-valued functions on Rn whose first k weak derivativeWeak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
s are functions in Lp
Lp space
In mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
. Here k is a non-negative integer and 1 ≤ p ≤ ∞. The first part of the Sobolev embedding theorem states that
if k > ℓ and 1 ≤ p < q ≤ ∞ are two extended real numbers such that (k-l)p < n and :
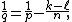
then
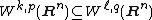
and the embedding is continuous. In the special case of k = 1 and ℓ = 0, Sobolev embedding gives
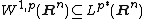
where p∗ is the Sobolev conjugate of p, given by
This special case of the Sobolev embedding is a direct consequence of the Gagliardo–Nirenberg–Sobolev inequality.
The second part of the Sobolev embedding theorem applies to embeddings in Hölder spaces Cr,α(Rn). If (k−r−α)/n = 1/p with α ∈ (0,1), then one has the embedding
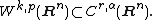
This part of the Sobolev embedding is a direct consequence of Morrey's inequality. Intuitively, this inclusion expresses the fact that the existence of sufficiently many weak derivatives implies some continuity of the classical derivatives.
Generalizations
The Sobolev embedding theorem holds for Sobolev spaces Wk,p(M) on other suitable domains M. In particular , both parts of the Sobolev embedding hold when
- M is a boundedBounded setIn mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
open setOpen setThe concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
in Rn with LipschitzLipschitz continuityIn mathematical analysis, Lipschitz continuity, named after Rudolf Lipschitz, is a strong form of uniform continuity for functions. Intuitively, a Lipschitz continuous function is limited in how fast it can change: for every pair of points on the graph of this function, the absolute value of the...
boundary (or whose boundary satisfies the cone condition; ) - M is a compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Riemannian manifoldRiemannian manifoldIn Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point... - M is a compact Riemannian manifold with boundary with Lipschitz boundary
- M is a complete Riemannian manifold with injectivity radius δ > 0 and bounded sectional curvatureSectional curvatureIn Riemannian geometry, the sectional curvature is one of the ways to describe the curvature of Riemannian manifolds. The sectional curvature K depends on a two-dimensional plane σp in the tangent space at p...
.
Kondrachov embedding theorem
On a compact manifold with C1 boundary, the Kondrachov embedding theorem states that if k> ℓ and k−n/p > ℓ−n/q then the Sobolev embedding
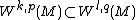
is completely continuous (compact).
Gagliardo–Nirenberg–Sobolev inequality
Assume that u is a continuously differentiable real-valued function on Rn with compact support. Then for 1 ≤ p < n there is a constant C depending only on n and p such that
where
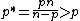
is the Sobolev conjugate of p.
The Gagliardo–Nirenberg–Sobolev inequality implies directly the Sobolev embedding
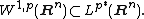
The embeddings in other orders on Rn are then obtained by suitable iteration.
Hardy–Littlewood–Sobolev lemma
Sobolev's original proof of the Sobolev embedding theorem relied on the following, sometimes known as the Hardy–Littlewood–Sobolev fractional integration theorem. An equivalent statement is known as the Sobolev lemma in . A proof is in .Let 0 < α
Riesz potential
In mathematics, the Riesz potential is a potential named after its discoverer, the Hungarian mathematician Marcel Riesz. In a sense, the Riesz potential defines an inverse for a power of the Laplace operator on Euclidean space...
on Rn. Then, for q defined by
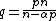
there exists a constant C depending only on p such that
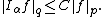
If p = 1, then the weak-type estimate holds:
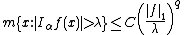
where 1/q = 1 − α/n.
The Hardy–Littlewood–Sobolev lemma implies the Sobolev embedding essentially by the relationship between the Riesz transforms and the Riesz potentials.
Morrey's inequality
Assume n < p ≤ ∞. Then there exists a constant C, depending only on p and n, such that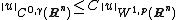for all u ∈ C1(Rn) ∩ Lp(Rn), where
Thus if u ∈ W1,p(Rn), then u is in fact Hölder continuous of exponent γ,
after possibly being redefined on a set of measure 0.
A similar result holds in a bounded domain U with C1 boundary. In this case,
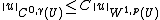
where the constant C depends now on n, p and U. This version of the inequality follows from the previous one by applying the norm-preserving extension of W1,p(U) to W1,p(Rn).
General Sobolev inequalities
Let U be a bounded open subset of Rn, with a C1 boundary. (U may also be unbounded, but in this case its boundary, if it exists, must be sufficiently well-behaved.) Assume u ∈ Wk,p(U).(i) If
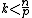
then
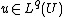, where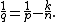We have in addition the estimate
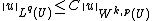,the constant C depending only on k, p, n, and U.
(ii) If
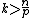
then u belongs to the Hölder space
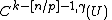, where 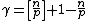if n/p is not an integer, or
- γ is any positive number < 1, if n/p is an integer
We have in addition the estimate
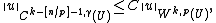
the constant C depending only on k, p, n, γ, and U.
Case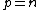 
If 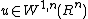, then is a function of bounded mean oscillationBounded mean oscillation
In harmonic analysis, a function of bounded mean oscillation, also known as a BMO function, is a real-valued function whose mean oscillation is bounded...
and
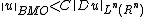, for some constant C depending only on n.This estimate is a corollary of the Poincaré inequality
Poincaré inequality
In mathematics, the Poincaré inequality is a result in the theory of Sobolev spaces, named after the French mathematician Henri Poincaré. The inequality allows one to obtain bounds on a function using bounds on its derivatives and the geometry of its domain of definition. Such bounds are of great...
.
Nash inequality
The Nash inequality, introduced by , states that there exists a constant C > 0, such that for all u ∈ L1(Rn) ∩ W1,2(Rn),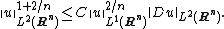The inequality follows from basic properties of the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
. Indeed, integrating over the complement of the ball of radius ρ,
by Parseval's theorem
Parseval's theorem
In mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum of the square of a function is equal to the sum of the square of its transform. It originates from a 1799 theorem about series by Marc-Antoine Parseval, which was later...
. On the other hand, one has
which, when integrated over the ball of radius ρ gives
where ωn is the volume of the n-ball. Choosing ρ to minimize the sum of and and again applying Parseval's theorem
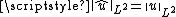gives the inequality.In the special case of n =1, the Nash inequality can be extended to the Lp case, in which case it is a generalization of the Gagliardo-Nirenberg-Sobolev inequality . In fact, if I is a bounded interval, then for all 1 ≤ r < ∞ and all 1 ≤ q ≤ p < ∞ the following inequality holds
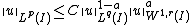
where a is defined by