Isoperimetric dimension
Encyclopedia
In mathematics
, the isoperimetric dimension of a manifold
is a notion of dimension that tries to capture how the large-scale behavior of the manifold resembles that of a Euclidean space
(unlike the topological dimension or the Hausdorff dimension
which compare different local behaviors against those of the Euclidean space).
In the Euclidean space
, the isoperimetric inequality
says that of all bodies with the same volume, the ball has the smallest surface area. In other manifolds it is usually very difficult to find the precise body minimizing the surface area, and this is not what the isoperimetric dimension is about. The question we will ask is, what is approximately the minimal surface area, whatever the body realizing it might be.
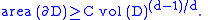
The notations vol and area refer to the regular notions of volume and surface area on the manifold, or more precisely, if the manifold has n topological dimensions then vol refers to n-dimensional volume and area refers to (n − 1)-dimensional volume. C here refers to some constant, which does not depend on D (it may depend on the manifold and on d).
The isoperimetric dimension of M is the supremum of all values of d such that M satisfies a d-dimensional isoperimetric inequality.
— as discussed above, for the Euclidean space the constant C is known precisely since the minimum is achieved for the ball.
An infinite cylinder (i.e. a product
of the circle
and the line
) has topological dimension 2 but isoperimetric dimension 1. Indeed, multiplying any manifold with a compact manifold does not change the isoperimetric dimension (it only changes the value of the constant C). Any compact manifold has isoperimetric dimension 0.
It is also possible for the isoperimetric dimension to be larger than the topological dimension. The simplest example is the infinite jungle gym
, which has topological dimension 2 and isoperimetric dimension 3. See http://www.math.ucla.edu/~bon/jungle.html for pictures and Mathematica code.
The hyperbolic plane
has topological dimension 2 and isoperimetric dimension infinity. In fact the hyperbolic plane has positive Cheeger constant
. This means that it satisfies the inequality
which obviously implies infinite isoperimetric dimension.
can be defined in a similar fashion. Area and volume are measured by set sizes. For every subset A of the graph G one defines
as the set of vertices in 
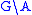with a neighbor in A. A d-dimensional isoperimetric inequality is now defined by
The graph analogs of all the examples above hold. The isoperimetric dimension of any finite graph is 0. The isoperimetric dimension of a d-dimensional grid is d. In general, the isoperimetric dimension is preserved by quasi isometries, both by quasi-isometries between manifolds, between graphs, and even by quasi isometries carrying manifolds to graphs, with the respective definitions. In rough terms, this means that a graph "mimicking" a given manifold (as the grid mimics the Euclidean space) would have the same isoperimetric dimension as the manifold. An infinite complete binary tree
has isoperimetric dimension ∞.
, namely
where B(x,r) denotes the ball of radius r around the point x in the Riemannian distance
or in the graph distance. In general, the opposite is not true, i.e. even uniformly exponential volume growth does not imply any kind of isoperimetric inequality. A simple example can be had by taking the graph Z (i.e. all the integers with edges between n and n + 1) and connecting to the vertex n a complete binary tree of height |n|. Both properties (exponential growth and 0 isoperimetric dimension) are easy to verify.
An interesting exception is the case of groups
. It turns out that a group with polynomial growth of order d has isoperimetric dimension d. This holds both for the case of Lie group
s and for the Cayley graph
of a finitely generated group.
A theorem of Varopoulos connects the isoperimetric dimension of a graph to the rate of escape of random walk
on the graph. The result states
Varopoulos' theorem: If G is a graph satisfying a d-dimensional isoperimetric inequality then
where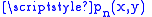
is the probability that a random walk on G starting from x will be in y after n steps, and C is some constant.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the isoperimetric dimension of a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
is a notion of dimension that tries to capture how the large-scale behavior of the manifold resembles that of a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(unlike the topological dimension or the Hausdorff dimension
Hausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
which compare different local behaviors against those of the Euclidean space).
In the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, the isoperimetric inequality
Isoperimetry
The isoperimetric inequality is a geometric inequality involving the square of the circumference of a closed curve in the plane and the area of a plane region it encloses, as well as its various generalizations. Isoperimetric literally means "having the same perimeter"...
says that of all bodies with the same volume, the ball has the smallest surface area. In other manifolds it is usually very difficult to find the precise body minimizing the surface area, and this is not what the isoperimetric dimension is about. The question we will ask is, what is approximately the minimal surface area, whatever the body realizing it might be.
Formal definition
We say about a manifold M that it satisfies a d-dimensional isoperimetric inequality if for any open set D in M with a smooth boundary one has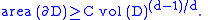The notations vol and area refer to the regular notions of volume and surface area on the manifold, or more precisely, if the manifold has n topological dimensions then vol refers to n-dimensional volume and area refers to (n − 1)-dimensional volume. C here refers to some constant, which does not depend on D (it may depend on the manifold and on d).
The isoperimetric dimension of M is the supremum of all values of d such that M satisfies a d-dimensional isoperimetric inequality.
Examples
A d-dimensional Euclidean space has isoperimetric dimension d. This is the well known isoperimetric problemIsoperimetry
The isoperimetric inequality is a geometric inequality involving the square of the circumference of a closed curve in the plane and the area of a plane region it encloses, as well as its various generalizations. Isoperimetric literally means "having the same perimeter"...
— as discussed above, for the Euclidean space the constant C is known precisely since the minimum is achieved for the ball.
An infinite cylinder (i.e. a product
Cartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
of the circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
and the line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
) has topological dimension 2 but isoperimetric dimension 1. Indeed, multiplying any manifold with a compact manifold does not change the isoperimetric dimension (it only changes the value of the constant C). Any compact manifold has isoperimetric dimension 0.
It is also possible for the isoperimetric dimension to be larger than the topological dimension. The simplest example is the infinite jungle gym
Jungle gym
The jungle gym, monkey bars, or climbing frame, is a piece of playground equipment made of many pieces of material, such as metal pipe or rope, on which children can climb, hang, or sit. The monkey bar designation refers to the rambunctious, climbing play of monkeys.-History:The first jungle gym...
, which has topological dimension 2 and isoperimetric dimension 3. See http://www.math.ucla.edu/~bon/jungle.html for pictures and Mathematica code.
The hyperbolic plane
Hyperbolic geometry
In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
has topological dimension 2 and isoperimetric dimension infinity. In fact the hyperbolic plane has positive Cheeger constant
Cheeger constant
In Riemannian geometry, the Cheeger isoperimetric constant of a compact Riemannian manifold M is a positive real number h defined in terms of the minimal area of a hypersurface that divides M into two disjoint pieces of equal volume...
. This means that it satisfies the inequality
which obviously implies infinite isoperimetric dimension.
Isoperimetric dimension of graphs
The isoperimetric dimension of graphsGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
can be defined in a similar fashion. Area and volume are measured by set sizes. For every subset A of the graph G one defines
as the set of vertices in 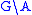with a neighbor in A. A d-dimensional isoperimetric inequality is now defined byThe graph analogs of all the examples above hold. The isoperimetric dimension of any finite graph is 0. The isoperimetric dimension of a d-dimensional grid is d. In general, the isoperimetric dimension is preserved by quasi isometries, both by quasi-isometries between manifolds, between graphs, and even by quasi isometries carrying manifolds to graphs, with the respective definitions. In rough terms, this means that a graph "mimicking" a given manifold (as the grid mimics the Euclidean space) would have the same isoperimetric dimension as the manifold. An infinite complete binary tree
Binary tree
In computer science, a binary tree is a tree data structure in which each node has at most two child nodes, usually distinguished as "left" and "right". Nodes with children are parent nodes, and child nodes may contain references to their parents. Outside the tree, there is often a reference to...
has isoperimetric dimension ∞.
Consequences of isoperimetry
A simple integration over r (or sum in the case of graphs) shows that a d-dimensional isoperimetric inequality implies a d-dimensional volume growthGrowth rate (group theory)
In group theory, the growth rate of a group with respect to a symmetric generating set describes the size of balls in the group. Every element in the group can be written as a product of generators, and the growth rate counts the number of elements that can be written as a product of length...
, namely
where B(x,r) denotes the ball of radius r around the point x in the Riemannian distance
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
or in the graph distance. In general, the opposite is not true, i.e. even uniformly exponential volume growth does not imply any kind of isoperimetric inequality. A simple example can be had by taking the graph Z (i.e. all the integers with edges between n and n + 1) and connecting to the vertex n a complete binary tree of height |n|. Both properties (exponential growth and 0 isoperimetric dimension) are easy to verify.
An interesting exception is the case of groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
. It turns out that a group with polynomial growth of order d has isoperimetric dimension d. This holds both for the case of Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
s and for the Cayley graph
Cayley graph
In mathematics, a Cayley graph, also known as a Cayley colour graph, Cayley diagram, group diagram, or colour group is a graph that encodes the abstract structure of a group. Its definition is suggested by Cayley's theorem and uses a specified, usually finite, set of generators for the group...
of a finitely generated group.
A theorem of Varopoulos connects the isoperimetric dimension of a graph to the rate of escape of random walk
Random walk
A random walk, sometimes denoted RW, is a mathematical formalisation of a trajectory that consists of taking successive random steps. For example, the path traced by a molecule as it travels in a liquid or a gas, the search path of a foraging animal, the price of a fluctuating stock and the...
on the graph. The result states
Varopoulos' theorem: If G is a graph satisfying a d-dimensional isoperimetric inequality then
where
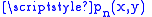is the probability that a random walk on G starting from x will be in y after n steps, and C is some constant.