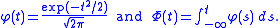Gaussian isoperimetric inequality
Encyclopedia
The Gaussian isoperimetric inequality, proved by Boris Tsirelson
and Vladimir Sudakov and independently by Christer Borell, states that among all sets of given Gaussian measure
in the n-dimensional Euclidean space
, half-space
s have the minimal Gaussian boundary measure
.
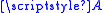 be a measurable subset of
be a measurable subset of 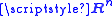 endowed with the Gaussian measure γ n. Denote by
endowed with the Gaussian measure γ n. Denote by
Boris Tsirelson
Boris Semyonovich Tsirelson is a Soviet-Israeli mathematician and Professor of Mathematics in the Tel Aviv University in Israel.-Biography:Boris Tsirelson was born in Leningrad to a Russian Jewish family...
and Vladimir Sudakov and independently by Christer Borell, states that among all sets of given Gaussian measure
Gaussian measure
In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
in the n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, half-space
Half-space
In geometry, a half-space is either of the two parts into which a plane divides the three-dimensional euclidean space. More generally, a half-space is either of the two parts into which a hyperplane divides an affine space...
s have the minimal Gaussian boundary measure
Minkowski content
The Minkowski content of a set, or the boundary measure, is a basic concept in geometry and measure theory which generalizes to arbitrary measurable sets the notions of length of a smooth curve in the plane and area of a smooth surface in the space...
.
Mathematical formulation
Let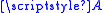 be a measurable subset of
be a measurable subset of 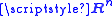 endowed with the Gaussian measure γ n. Denote by
endowed with the Gaussian measure γ n. Denote by
-
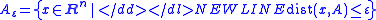
the ε-extension of A. Then the Gaussian isoperimetric inequality states that
-
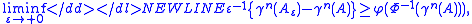
where
Remarks on the proofs
The original proofs by Sudakov, Tsirelson and Borell were based on Paul LévyPaul Pierre LévyPaul Pierre Lévy was a Jewish French mathematician who was active especially in probability theory, introducing martingales and Lévy flights...
's spherical isoperimetric inequality. Another approach is due to Bobkov, who introduced a functional inequality generalizing the Gaussian isoperimetric inequality and derived it from a certain two-point inequality. Bakry and Ledoux gave another proof of Bobkov's functional inequality based on the semigroupSemigroupIn mathematics, a semigroup is an algebraic structure consisting of a set together with an associative binary operation. A semigroup generalizes a monoid in that there might not exist an identity element...
techniques which works in a much more abstract setting. Later Barthe and Maurey gave yet another proof using the Brownian motionBrownian motionBrownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
.
The Gaussian isoperimetric inequality also follows from Ehrhard's inequality (cf. Latała [6], Borell [7]). -
-