The circumference is the distance around a closed curve. Circumference is a special perimeter

Perimeter

A perimeter is a path that surrounds an area. The word comes from the Greek peri and meter . The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circular area is called circumference.- Practical uses :Calculating...

.

Circumference of a circle

The circumference of a circle is the length around it.
The circumference of a circle

Circle

A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....

 can be calculated from its diameter

Diameter

In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints are on the circle. The diameters are the longest chords of the circle...

 using the formula:


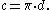
Or, substituting the radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

 for the diameter:


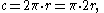
where is the radius

Radius

In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...

 and is the diameter of the circle, and the Greek letter is defined as the ratio of the circumference of the circle to its diameter. The numerical value of is 3.141 592 653 589 793....

Circumference of an ellipse

The circumference of an ellipse

Ellipse

In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...

 is more problematic, as the exact solution requires finding the complete elliptic integral of the second kind. This can be achieved either via numerical integration

Numerical integration

In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...

 (the best type being Gaussian quadrature

Gaussian quadrature

In numerical analysis, a quadrature rule is an approximation of the definite integral of a function, usually stated as a weighted sum of function values at specified points within the domain of integration....

) or by one of many binomial series

Binomial series

In mathematics, the binomial series is the Taylor series at x = 0 of the function f given by f =  α, where is an arbitrary complex number...

 expansions.

Where , are the ellipse's semi-major

Semi-major axis

The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...

 and semi-minor

Semi-minor axis

In geometry, the semi-minor axis is a line segment associated with most conic sections . One end of the segment is the center of the conic section, and it is at right angles with the semi-major axis...

 axes, respectively, and is the ellipse's angular eccentricity

Angular eccentricity

In the study of ellipses and related geometry, various parameters in the distortion of a circle into an ellipse are identified and employed: Aspect ratio, flattening and eccentricity....

,





There are many different approximation

Approximation

An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...

s for the divided difference

Difference quotient

The primary vehicle of calculus and other higher mathematics is the function. Its "input value" is its argument, usually a point expressible on a graph...

, with varying degrees of sophistication and corresponding accuracy.

In comparing the different approximations, the 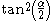(also known as "", the third flattening

Flattening

The flattening, ellipticity, or oblateness of an oblate spheroid is a measure of the "squashing" of the spheroid's pole, towards its equator...

 of the ellipse) based series expansion is used to find the actual value:



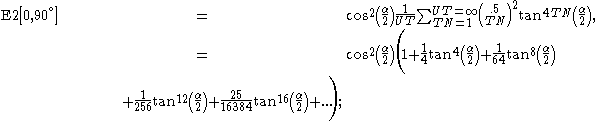
More generally, the arc length

Arc length

Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...

 of a portion of the circumference, as a function of the angle subtended, is given by an incomplete elliptic integral

Elliptic integral

In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...

.

The inverse function

Inverse function

In mathematics, an inverse function is a function that undoes another function: If an input x into the function ƒ produces an output y, then putting y into the inverse function g produces the output x, and vice versa. i.e., ƒ=y, and g=x...

, the angle subtended as a function of the arc length, is given by the elliptic functions.

Muir-1883

Probably the most accurate to its given simplicity is Thomas Muir's

Thomas Muir (mathematician)

Sir Thomas Muir FRS was a Scottish mathematician, remembered as an authority on determinants. He was born in Stonebyres in South Lanarkshire, and brought up in the small town of Biggar. At the University of Glasgow he changed his studies from classics to mathematics after advice from the future...

:

Ramanujan-1914 (#1,#2)

Srinivasa Ramanujan

Srinivasa Ramanujan

Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...

 introduced two different approximations, both from 1914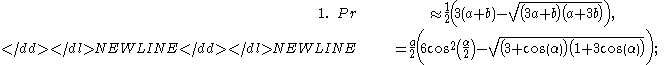

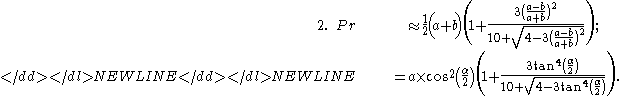
The second equation is demonstrably by far the better of the two, and may be the most accurate approximation known.

Letting = 10000 and = ×cos{}, results with different ellipticities can be found and compared:

b	Pr	Ramanujan-#2	Ramanujan-#1	Muir
9975	9987.50391 11393	9987.50391 11393	9987.50391 11393	9987.50391 11389
9966	9983.00723 73047	9983.00723 73047	9983.00723 73047	9983.00723 73034
9950	9975.01566 41666	9975.01566 41666	9975.01566 41666	9975.01566 41604
9900	9950.06281 41695	9950.06281 41695	9950.06281 41695	9950.06281 40704
9000	9506.58008 71725	9506.58008 71725	9506.58008 67774	9506.57894 84209
8000	9027.79927 77219	9027.79927 77219	9027.79924 43886	9027.77786 62561
7500	8794.70009 24247	8794.70009 24240	8794.69994 52888	8794.64324 65132
6667	8417.02535 37669	8417.02535 37460	8417.02428 62059	8416.81780 56370
5000	7709.82212 59502	7709.82212 24348	7709.80054 22510	7708.38853 77837
3333	7090.18347 61693	7090.18324 21686	7089.94281 35586	7083.80287 96714
2500	6826.49114 72168	6826.48944 11189	6825.75998 22882	6814.20222 31205
1000	6468.01579 36089	6467.94103 84016	6462.57005 00576	6431.72229 28418
100	6367.94576 97209	6366.42397 74408	6346.16560 81001	6303.80428 66621
10	6366.22253 29150	6363.81341 42880	6340.31989 06242	6299.73805 61141
1	6366.19804 50617	6363.65301 06191	6339.80266 34498	6299.60944 92105
iota Iota Iota is the ninth letter of the Greek alphabet. In the system of Greek numerals it has a value of 10. It was derived from the Phoenician letter Yodh . Letters that arose from this letter include the Roman I and J and the Cyrillic І , Yi , Je , and iotified letters .Iota represents...	6366.19772 36758	6363.63636 36364	6339.74596 21556	6299.60524 94744

Circumference of a graph

In graph theory

Graph theory

In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...

 the circumference of a graph

Graph (mathematics)

In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...

 refers to the longest cycle

Cycle (graph theory)

In graph theory, the term cycle may refer to a closed path. If repeated vertices are allowed, it is more often called a closed walk. If the path is a simple path, with no repeated vertices or edges other than the starting and ending vertices, it may also be called a simple cycle, circuit, circle,...

contained in that graph.

External links

• Numericana - Circumference of an ellipse
• Circumference of a circle With interactive applet and animation

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.