
Hausdorff measure
Encyclopedia
In mathematics
a Hausdorff measure is a type of outer measure
, named for Felix Hausdorff
, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space
. The zero dimensional Hausdorff measure is the number of points in the set (if the set is finite) or ∞ if the set is infinite. The one dimensional Hausdorff measure of a simple curve in Rn is equal to the length of the curve. Likewise, the two dimensional Hausdorff measure of a measurable subset of R2 is proportional to the area of the set. Thus, the concept of the Hausdorff measure generalizes counting, length, and area. It also generalizes volume. In fact, there are d-dimensional Hausdorff measures for any d ≥ 0, which is not necessarily an integer. These measures are fundamental in geometric measure theory
. They appear naturally in harmonic analysis
or potential theory
.
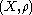 be a metric space. For any subset
be a metric space. For any subset  , let
, let  denote its diameter, that is
denote its diameter, that is

Let be any subset of
be any subset of 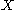 , and
, and  a real number. Define
a real number. Define
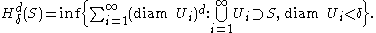
(The infimum is over all countable covers of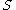 by sets
by sets 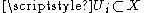 satisfying
satisfying  .)
.)
Note that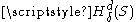 is monotone decreasing in δ since the larger δ is, the more collections of sets are permitted, making the infimum smaller. Thus, the limit
is monotone decreasing in δ since the larger δ is, the more collections of sets are permitted, making the infimum smaller. Thus, the limit 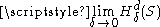 exists but may be infinite. Let
exists but may be infinite. Let
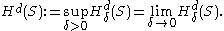
It can be seen that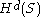 is an outer measure
is an outer measure
(more precisely, it is a metric outer measure
). By general theory, its restriction to the σ-field of Caratheodory-measurable sets is a measure. It is called the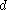 -dimensional Hausdorff measure of
-dimensional Hausdorff measure of  . Due to the metric outer measure
. Due to the metric outer measure
property, all Borel subsets of are
are  measurable.
measurable.
In the above definition the sets in the covering are arbitrary. However, they may be taken to be open or closed, and will yield the same measure, although the approximations may be different . If
may be different . If 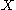 is a normed space the sets may be taken to be convex. However, the restriction of the covering families to balls gives a different measure.
is a normed space the sets may be taken to be convex. However, the restriction of the covering families to balls gives a different measure.
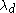 which is normalized so that the Lebesgue measure of the unit cube [0,1]d is 1. In fact, for any Borel set E,
which is normalized so that the Lebesgue measure of the unit cube [0,1]d is 1. In fact, for any Borel set E,
where αd is the volume of the unit d-ball,
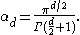
Remark. Some authors adopt a definition of Hausdorff measure slightly different from the one chosen here, the difference being that it is normalized in such a way that Hausdorff d-dimensional measure in the case of Euclidean space coincides exactly with Lebesgue measure.
is

where we take

and related fields, the Minkowski content
is often used to measure the size of a subset of a metric measure space. For suitable domains in Euclidean space, the two notions of size coincide, up to overall normalizations depending on conventions. More precisely, a subset of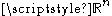 is said to be
is said to be  -rectifiable
-rectifiable
if it is the image of a bounded set
in under a Lipschitz function. If
under a Lipschitz function. If  , then the
, then the 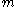 -dimensional Minkowski content of a closed
-dimensional Minkowski content of a closed  -rectifiable subset of
-rectifiable subset of 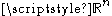 is equal to
is equal to  times the
times the 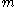 -dimensional Hausdorff measure .
-dimensional Hausdorff measure .
In fractal geometry, some fractals with Hausdorff dimension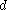 have zero or infinite
have zero or infinite 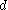 -dimensional Hausdorff measure. For example, almost surely
-dimensional Hausdorff measure. For example, almost surely
the image of planar Brownian motion
has Hausdorff dimension 2 and its two-dimensional Hausdoff measure is zero. In order to “measure” the “size” of such sets, mathematicians have considered the following variation on the notion of the Hausdorff measure.
In the definition of the measure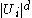 is replaced with
is replaced with  where
where 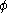 is any monotone increasing function
is any monotone increasing function  satisfying
satisfying  .
.
This is the Hausdorff measure of with gauge function
with gauge function 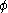 or
or  -Hausdorff measure. A
-Hausdorff measure. A  -dimensional set
-dimensional set  may satisfy
may satisfy  , but
, but 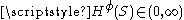 with an appropriate
with an appropriate 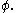 Examples of gauge functions include
Examples of gauge functions include 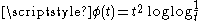 or
or 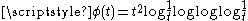 . The former gives almost surely positive and
. The former gives almost surely positive and  -finite measure to the Brownian path in
-finite measure to the Brownian path in  when
when  , and the latter when
, and the latter when 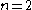 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a Hausdorff measure is a type of outer measure
Outer measure
In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
, named for Felix Hausdorff
Felix Hausdorff
Felix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...
, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
. The zero dimensional Hausdorff measure is the number of points in the set (if the set is finite) or ∞ if the set is infinite. The one dimensional Hausdorff measure of a simple curve in Rn is equal to the length of the curve. Likewise, the two dimensional Hausdorff measure of a measurable subset of R2 is proportional to the area of the set. Thus, the concept of the Hausdorff measure generalizes counting, length, and area. It also generalizes volume. In fact, there are d-dimensional Hausdorff measures for any d ≥ 0, which is not necessarily an integer. These measures are fundamental in geometric measure theory
Geometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
. They appear naturally in harmonic analysis
Harmonic analysis
Harmonic analysis is the branch of mathematics that studies the representation of functions or signals as the superposition of basic waves. It investigates and generalizes the notions of Fourier series and Fourier transforms...
or potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
.
Definition
Let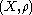 be a metric space. For any subset
be a metric space. For any subset  , let
, let  denote its diameter, that is
denote its diameter, that is
Let
 be any subset of
be any subset of 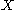 , and
, and  a real number. Define
a real number. Define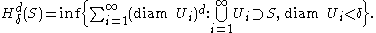
(The infimum is over all countable covers of
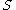 by sets
by sets 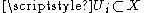 satisfying
satisfying  .)
.)Note that
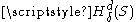 is monotone decreasing in δ since the larger δ is, the more collections of sets are permitted, making the infimum smaller. Thus, the limit
is monotone decreasing in δ since the larger δ is, the more collections of sets are permitted, making the infimum smaller. Thus, the limit 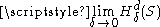 exists but may be infinite. Let
exists but may be infinite. Let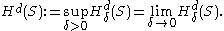
It can be seen that
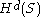 is an outer measure
is an outer measureOuter measure
In mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
(more precisely, it is a metric outer measure
Metric outer measure
In mathematics, a metric outer measure is an outer measure μ defined on the subsets of a given metric space such that\mu = \mu + \mu for every pair of positively separated subsets A and B of X....
). By general theory, its restriction to the σ-field of Caratheodory-measurable sets is a measure. It is called the
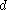 -dimensional Hausdorff measure of
-dimensional Hausdorff measure of  . Due to the metric outer measure
. Due to the metric outer measureMetric outer measure
In mathematics, a metric outer measure is an outer measure μ defined on the subsets of a given metric space such that\mu = \mu + \mu for every pair of positively separated subsets A and B of X....
property, all Borel subsets of
 are
are  measurable.
measurable.In the above definition the sets in the covering are arbitrary. However, they may be taken to be open or closed, and will yield the same measure, although the approximations
 may be different . If
may be different . If 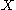 is a normed space the sets may be taken to be convex. However, the restriction of the covering families to balls gives a different measure.
is a normed space the sets may be taken to be convex. However, the restriction of the covering families to balls gives a different measure.Properties of Hausdorff measures
Note that if d is a positive integer, the d dimensional Hausdorff measure of Rd is a rescaling of usual d-dimensional Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
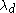 which is normalized so that the Lebesgue measure of the unit cube [0,1]d is 1. In fact, for any Borel set E,
which is normalized so that the Lebesgue measure of the unit cube [0,1]d is 1. In fact, for any Borel set E,
where αd is the volume of the unit d-ball,
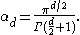
Remark. Some authors adopt a definition of Hausdorff measure slightly different from the one chosen here, the difference being that it is normalized in such a way that Hausdorff d-dimensional measure in the case of Euclidean space coincides exactly with Lebesgue measure.
Relation with Hausdorff dimension
One of several possible equivalent definitions of the Hausdorff dimensionHausdorff dimension
thumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
is

where we take

Generalizations
In geometric measure theoryGeometric measure theory
In mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
and related fields, the Minkowski content
Minkowski content
The Minkowski content of a set, or the boundary measure, is a basic concept in geometry and measure theory which generalizes to arbitrary measurable sets the notions of length of a smooth curve in the plane and area of a smooth surface in the space...
is often used to measure the size of a subset of a metric measure space. For suitable domains in Euclidean space, the two notions of size coincide, up to overall normalizations depending on conventions. More precisely, a subset of
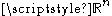 is said to be
is said to be  -rectifiable
-rectifiableRectifiable set
In mathematics, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set...
if it is the image of a bounded set
Bounded set
In mathematical analysis and related areas of mathematics, a set is called bounded, if it is, in a certain sense, of finite size. Conversely, a set which is not bounded is called unbounded...
in
 under a Lipschitz function. If
under a Lipschitz function. If  , then the
, then the 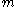 -dimensional Minkowski content of a closed
-dimensional Minkowski content of a closed  -rectifiable subset of
-rectifiable subset of 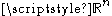 is equal to
is equal to  times the
times the 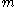 -dimensional Hausdorff measure .
-dimensional Hausdorff measure .In fractal geometry, some fractals with Hausdorff dimension
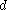 have zero or infinite
have zero or infinite 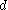 -dimensional Hausdorff measure. For example, almost surely
-dimensional Hausdorff measure. For example, almost surelyAlmost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
the image of planar Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
has Hausdorff dimension 2 and its two-dimensional Hausdoff measure is zero. In order to “measure” the “size” of such sets, mathematicians have considered the following variation on the notion of the Hausdorff measure.
In the definition of the measure
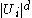 is replaced with
is replaced with  where
where 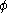 is any monotone increasing function
is any monotone increasing function  satisfying
satisfying  .
.This is the Hausdorff measure of
 with gauge function
with gauge function 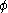 or
or  -Hausdorff measure. A
-Hausdorff measure. A  -dimensional set
-dimensional set  may satisfy
may satisfy  , but
, but 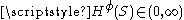 with an appropriate
with an appropriate 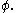 Examples of gauge functions include
Examples of gauge functions include 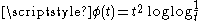 or
or 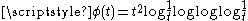 . The former gives almost surely positive and
. The former gives almost surely positive and  -finite measure to the Brownian path in
-finite measure to the Brownian path in  when
when  , and the latter when
, and the latter when 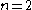 .
.

