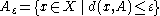Minkowski content
Encyclopedia
The Minkowski
content of a set, or the boundary measure, is a basic concept in geometry
and measure theory which generalizes to arbitrary measurable sets the notions of length
of a smooth curve in the plane and area
of a smooth surface in the space
. It is typically applied to fractal
boundaries of domains in the Euclidean space
, but makes sense in the context of general metric measure spaces. It is related to, although different from, the Hausdorff measure
.
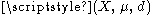 be a metric measure space, where d is a metric
be a metric measure space, where d is a metric
on X and μ is a Borel measure. For a subset A of X and real ε > 0, let
be the ε-extension of A. The lower Minkowski content of A is given by

and the upper Minkowski content of A is

If M*(A) = M*(A), then the common value is called the Minkowski content of A associated with the measure μ, and is denoted by M(A).

where αn−m is the volume of the unit (n−m)-ball and is
is  -dimensional Lebesgue measure
-dimensional Lebesgue measure
. The upper content is
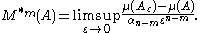
As before, if the upper and lower m-dimensional Minkowski content of A agree, then the Minkowski content of A, Mm(A), is defined to be this common value.
Hermann Minkowski
Hermann Minkowski was a German mathematician of Ashkenazi Jewish descent, who created and developed the geometry of numbers and who used geometrical methods to solve difficult problems in number theory, mathematical physics, and the theory of relativity.- Life and work :Hermann Minkowski was born...
content of a set, or the boundary measure, is a basic concept in geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and measure theory which generalizes to arbitrary measurable sets the notions of length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
of a smooth curve in the plane and area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
of a smooth surface in the space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. It is typically applied to fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
boundaries of domains in the Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, but makes sense in the context of general metric measure spaces. It is related to, although different from, the Hausdorff measure
Hausdorff measure
In mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
.
Definition
Let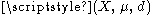 be a metric measure space, where d is a metric
be a metric measure space, where d is a metricMetric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
on X and μ is a Borel measure. For a subset A of X and real ε > 0, let
be the ε-extension of A. The lower Minkowski content of A is given by

and the upper Minkowski content of A is

If M*(A) = M*(A), then the common value is called the Minkowski content of A associated with the measure μ, and is denoted by M(A).
Minkowski content in Rn
Let A be a subset of Rn. Then the m-dimensional Minkowski content of A is defined as follows. The lower content is
where αn−m is the volume of the unit (n−m)-ball and
 is
is  -dimensional Lebesgue measure
-dimensional Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
. The upper content is
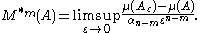
As before, if the upper and lower m-dimensional Minkowski content of A agree, then the Minkowski content of A, Mm(A), is defined to be this common value.
Properties
- The Minkowski content is (generally) not a measure. In particular, the m-dimensional Minkowski content in Rn is not a measure unless m = 0, in which case it is the counting measureCounting measureIn mathematics, the counting measure is an intuitive way to put a measure on any set: the "size" of a subset is taken to be the number of elements in the subset, if the subset is finite, and ∞ if the subset is infinite....
. Indeed, clearly the Minkowski content assigns the same value to the set A as well as its closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
. - If A is a closed m-rectifiable setRectifiable setIn mathematics, a rectifiable set is a set that is smooth in a certain measure-theoretic sense. It is an extension of the idea of a rectifiable curve to higher dimensions; loosely speaking, a rectifiable set is a rigorous formulation of a piece-wise smooth set...
in Rn, given as the image of a bounded set from Rm under a Lipschitz function, then the m-dimensional Minkowski content of A exists, and is equal to the m-dimensional Hausdorff measureHausdorff measureIn mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
of A, apart from a constant normalization depending on the dimension.
See also
- Gaussian isoperimetric inequality
- Geometric measure theoryGeometric measure theoryIn mathematics, geometric measure theory is the study of the geometric properties of the measures of sets , including such things as arc lengths and areas. It uses measure theory to generalize differential geometry to surfaces with mild singularities called rectifiable sets...
- Isoperimetric problemIsoperimetric problemIsoperimetric problem may refer to:* Isoperimetric inequality* Any problem in calculus of variations...
- Minkowski–Bouligand dimension