In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, specifically commutative algebra

Commutative algebra

Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...

, a proper ideal

Ideal (ring theory)

In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....

 Q of a commutative ring

Commutative ring

In ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....

 A is said to be primary if whenever xy is an element of Q then x or yⁿ is also an element of Q, for some n. For example, in the ring of integers

Ring of integers

In mathematics, the ring of integers is the set of integers making an algebraic structure Z with the operations of integer addition, negation, and multiplication...

 Z, (pⁿ) is a primary ideal if p is a prime number.

The notion of primary ideals is important in commutative ring theory because every ideal of a Noetherian ring

Noetherian ring

In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...

 has a primary decomposition, that is, can be written as an intersection of finitely many primary ideals. This result is known as the Lasker–Noether theorem

Lasker–Noether theorem

In mathematics, the Lasker–Noether theorem states that every Noetherian ring is a Lasker ring, which means that every ideal can be written as an intersection of finitely many primary ideals...

. Consequently, an irreducible ideal

Irreducible ideal

In mathematics, an ideal of a commutative ring is said to be irreducible if it cannot be written as a finite intersection of ideals properly containing it....

 of a Noetherian ring is primary.

Various methods of generalizing primary ideals to noncommutative rings exist but the topic is most often studied for commutative rings. Therefore, the rings in this article are assumed to be commutative rings with identity.

Examples and properties

• Any prime ideal
  Prime ideal
  In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
  
   is primary, and moreover an ideal is prime if and only if it is primary and semiprime.

• Every primary ideal is primal
  Primal ideal
  In mathematics, an element a of a commutative ring A is called prime to an ideal Q if whenever ab is an element of Q then b is also an element of Q....
  
  .

• If Q is a primary ideal, then the radical
  Radical of an ideal
  In commutative ring theory, a branch of mathematics, the radical of an ideal I is an ideal such that an element x is in the radical if some power of x is in I. A radical ideal is an ideal that is its own radical...
  
   of Q is necessarily a prime ideal P, and this ideal is called the associated prime ideal of Q. In this situation, Q is said to be P-primary.

• If P is a maximal prime ideal, then any ideal containing a power of P is P-primary. Not all P-primary ideals need be powers of P; for example the ideal (x, y²) is P-primary for the ideal P = (x, y) in the ring k[x, y], but is not a power of P.

• In general powers of a prime ideal P need not be P-primary. (An example is given by taking R to be the ring k[x, y, z]/(xy − z²), with P the prime ideal (x, z). If Q = P², then xy ∈ Q, but x is not in Q and y is not in the radical P of Q, so Q is not P-primary.) However every ideal Q with radical P is contained in a smallest P-primary ideal, consisting of all elements a such that ax is in Q for some x not in P. In particular there is a smallest P-primary ideal containing Pⁿ, called the nth symbolic power of P.

• If A is a Noetherian ring
  Noetherian ring
  In mathematics, more specifically in the area of modern algebra known as ring theory, a Noetherian ring, named after Emmy Noether, is a ring in which every non-empty set of ideals has a maximal element...
  
  and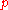 a prime ideal, then the kernel of 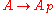is the intersection of all 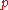-primary ideals.

External links

• Primary ideal at Encyclopaedia of Mathematics