Norm of an ideal
Encyclopedia
In commutative algebra
, the norm of an ideal is a generalization of a norm
of an element in the field extension. It is particularly important in number theory since it measures the size of an ideal
of a complicated number ring in terms of an ideal in a less complicated ring. When the less complicated number ring is taken to be the ring of integers, Z, then the norm of a nonzero ideal I of a number ring R is simply the size of the finite quotient ring
R/I.
with the field of fractions
K and B be the integral closure of A in a finite separable extension
L of K. (In particular, B is Dedekind then.) Let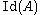
and 
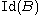be the ideal groups of A and B, respectively (i.e., the sets of fractional ideal
s.) Following , the norm map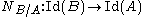
is a homomorphism given by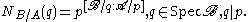
If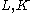
are local fields, 
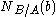is defined to be a fractional ideal generated by the set 
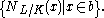This definition is equivalent to the above and is given in .
For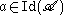
, one has 
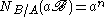where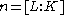 
. The definition is also compatible with norm of an element: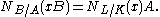 
Let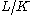
be a finite Galois extension of number fields with rings of integers 
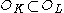. Then the preceding applies with 
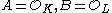and one has
which is an ideal of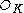
. The norm of a principal ideal
generated by α is the ideal generated by the field norm
of α.
The norm map is defined from the set of ideals of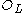
to the set of ideals of 
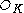. It is reasonable to use integers as the range for 
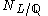since Z has trivial ideal class group
. This idea does not work in general since the class group may not be trivial.
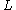be a number field
with ring of integers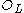
, and 
a nonzero ideal of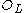 
. Then the norm of 
is defined to be
By convention, the norm of the zero ideal is taken to be zero.
If
is a principal ideal with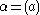 
, then 
.
The norm is also completely multiplicative
in that if
and 
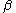are ideals of 
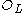, then 
.
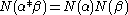The norm of an ideal
can be used to bound the norm of some nonzero element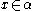 
by the inequality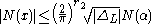
where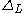
is the discriminant
of
and 
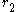is the number of pairs of complex embeddings of 
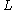into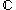 
.
Commutative algebra
Commutative algebra is the branch of abstract algebra that studies commutative rings, their ideals, and modules over such rings. Both algebraic geometry and algebraic number theory build on commutative algebra...
, the norm of an ideal is a generalization of a norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
of an element in the field extension. It is particularly important in number theory since it measures the size of an ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of a complicated number ring in terms of an ideal in a less complicated ring. When the less complicated number ring is taken to be the ring of integers, Z, then the norm of a nonzero ideal I of a number ring R is simply the size of the finite quotient ring
Quotient ring
In ring theory, a branch of modern algebra, a quotient ring, also known as factor ring or residue class ring, is a construction quite similar to the factor groups of group theory and the quotient spaces of linear algebra...
R/I.
Relative norm
Let A be a Dedekind domainDedekind domain
In abstract algebra, a Dedekind domain or Dedekind ring, named after Richard Dedekind, is an integral domain in which every nonzero proper ideal factors into a product of prime ideals. It can be shown that such a factorization is then necessarily unique up to the order of the factors...
with the field of fractions
Field of fractions
In abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
K and B be the integral closure of A in a finite separable extension
Separable extension
In modern algebra, an algebraic field extension E\supseteq F is a separable extension if and only if for every \alpha\in E, the minimal polynomial of \alpha over F is a separable polynomial . Otherwise, the extension is called inseparable...
L of K. (In particular, B is Dedekind then.) Let
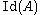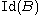and be the ideal groups of A and B, respectively (i.e., the sets of fractional idealFractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
s.) Following , the norm map
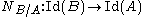
is a homomorphism given by
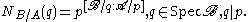
If
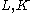are local fields, 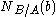is defined to be a fractional ideal generated by the set 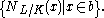This definition is equivalent to the above and is given in .For
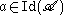, one has 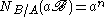where 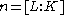. The definition is also compatible with norm of an element: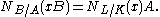 Let
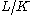be a finite Galois extension of number fields with rings of integers 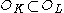. Then the preceding applies with 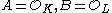and one haswhich is an ideal of
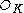. The norm of a principal idealPrincipal ideal
In ring theory, a branch of abstract algebra, a principal ideal is an ideal I in a ring R that is generated by a single element a of R.More specifically:...
generated by α is the ideal generated by the field norm
Field norm
In mathematics, the norm is a mapping defined in field theory, to map elements of a larger field into a smaller one.-Formal definitions:1. Let K be a field and L a finite extension of K...
of α.
The norm map is defined from the set of ideals of
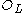to the set of ideals of 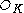. It is reasonable to use integers as the range for 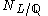since Z has trivial ideal class groupIdeal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
. This idea does not work in general since the class group may not be trivial.
Absolute norm
Let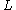 be a number fieldAlgebraic number field
In mathematics, an algebraic number field F is a finite field extension of the field of rational numbers Q...
with ring of integers
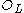, and a nonzero ideal of 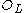. Then the norm of is defined to beBy convention, the norm of the zero ideal is taken to be zero.
If
is a principal ideal with 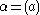, then .The norm is also completely multiplicative
Completely multiplicative function
In number theory, functions of positive integers which respect products are important and are called completely multiplicative functions or totally multiplicative functions. Especially in number theory, a weaker condition is also important, respecting only products of coprime numbers, and such...
in that if
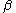and are ideals of 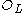, then 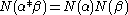.The norm of an ideal
can be used to bound the norm of some nonzero element 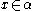by the inequality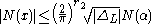where
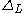is the discriminantDiscriminant of an algebraic number field
In mathematics, the discriminant of an algebraic number field is a numerical invariant that, loosely speaking, measures the size of the algebraic number field...
of
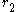and is the number of pairs of complex embeddings of 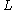into 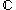.