
Gravitational wave
Encyclopedia
In physics
, gravitational waves are theoretical ripples in the curvature
of spacetime
which propagates as a wave
, traveling outward from the source. Predicted to exist by Albert Einstein
in 1916 on the basis of his theory of general relativity
, gravitational waves theoretically transport energy as gravitational radiation. Sources of gravitational waves could possibly include binary star
systems composed of white dwarfs, neutron stars, or black holes. The existence of gravitational waves is possibly a consequence of the Lorentz invariance of general relativity
since it brings the concept of a limiting speed of propagation of the physical interactions with it. Gravitational waves cannot exist in the Newtonian theory of gravitation, since in it physical interactions propagate at infinite speed.
Although gravitational radiation has not been directly detected, there is indirect evidence for its existence. For example, the 1993 Nobel Prize in Physics
was awarded for measurements of the Hulse-Taylor binary system which suggests gravitational waves are more than mathematical anomalies. Various gravitational wave detectors exist. However, they remain unsuccessful in detecting such phenomena.
, gravity is treated as a phenomenon resulting in the curvature of spacetime
. This curvature is caused by the presence of massive objects. Roughly speaking, the more massive the object is, the greater the curvature it produces and hence the more intense the gravity. As massive objects move around in spacetime, the curvature changes to reflect the changed locations of those objects. In certain circumstances, objects that are accelerated
generate a disturbance in spacetime which spreads, as the metaphor goes, "like ripples on the surface of a pond", although perhaps a better analogy would be electromagnetic waves. This disturbance is known as gravitational radiation. Gravitational radiation is thought to travel through the Universe at the speed of light
, diminishing in strength but never stopping or slowing down.
As waves of gravitational radiation pass a distant observer, that observer will find spacetime distorted by the effects of strain. Distances between free objects will increase and decrease rhythmically as the wave passes. The magnitude of this effect will decrease the farther the observer is from the source. Binary neutron star
s are predicted to be a strong source of such waves owing to the acceleration of their enormous masses as they orbit
each other and yet even those waves are expected to be very weak by the time they reach the Earth, resulting in strains of less than 1 part in 1020. Scientists are attempting to demonstrate the existence of these waves with ever more sensitive detectors. The current most sensitive measurement is about one part in 3 x 1022 (as of 2007) provided by the LIGO
detector. Sources this intense are not expected to last long so is merely a matter of luck if any are found. Another attempt, still under development, is Laser Interferometer Space Antenna
, a joint effort of NASA and ESA.
Gravitational waves should penetrate regions of space that electromagnetic waves cannot. It is hypothesized that they will be able to provide observers on Earth with information about black holes and other mysterious objects in the distant Universe. Such systems cannot be observed with more traditional means such as optical telescope
s and radio telescope
s. In particular, gravitational waves could be of interest to cosmologists as they offer a possible way of observing the very early universe. This is not possible with conventional astronomy, since before recombination
the universe was opaque to electromagnetic radiation. Precise measurements of gravitational waves will also allow scientists to test the general theory of relativity more thoroughly.
In principle, gravitational waves could exist at any frequency. However, very low frequency waves would be impossible to detect and there is no credible source for detectable waves of very high frequency. Stephen W. Hawking
and Werner Israel
list different frequency bands for gravitational waves that could be plausibly detected, ranging from 10−7 Hz up to 1011 Hz.

 Imagine a perfectly flat region of spacetime with a group of motionless test particles lying in a plane (the surface of your screen). Then a weak gravitational wave arrives, passing through the particles along a line perpendicular to the plane of the particles (i.e. following your line of vision into the screen). The particles will oscillate in a "cruciform
Imagine a perfectly flat region of spacetime with a group of motionless test particles lying in a plane (the surface of your screen). Then a weak gravitational wave arrives, passing through the particles along a line perpendicular to the plane of the particles (i.e. following your line of vision into the screen). The particles will oscillate in a "cruciform
" manner, as shown in the animations. The area enclosed by the test particles does not change and there is no motion along the direction of propagation.
The oscillations depicted here in the animation are of course immensely exaggerated for the purpose of discussion—in reality a gravitational wave has a very small amplitude (as formulated in linearized gravity
). However they enable us to visualize the kind of oscillations associated with gravitational waves as produced for example by a pair of masses in a circular orbit
. In this case the amplitude of the gravitational wave is a constant, but its plane of polarization changes or rotates at twice the orbital rate and so the time-varying gravitational wave size (or 'periodic spacetime strain') exhibits a variation as shown in the animation. If the orbit is elliptical then the gravitational wave's amplitude also varies with time according to an equation called the "quadrupole
".
Like other wave
s, there are a few useful characteristics describing a gravitational wave:
The speed, wavelength, and frequency of a gravitational wave are related by the equation c = λ f, just like the equation for a light wave. For example, the animations shown here oscillate roughly once every two seconds. This would correspond to a frequency of 0.5 Hz, and a wavelength of about 600,000 km, or 47 times the diameter of the Earth.
In the example just discussed, we actually assume something special about the wave. We have assumed that the wave is linearly polarized
, with a "plus" polarization, written . Polarization of a gravitational wave is just like polarization of a light wave except that the polarizations of a gravitational wave are at 45 degrees, as opposed to 90 degrees. In particular, if we had a "cross"-polarized gravitational wave,
. Polarization of a gravitational wave is just like polarization of a light wave except that the polarizations of a gravitational wave are at 45 degrees, as opposed to 90 degrees. In particular, if we had a "cross"-polarized gravitational wave,  , the effect on the test particles would be basically the same, but rotated by 45 degrees, as shown in the second animation. Just as with light polarization, the polarizations of gravitational waves may also be expressed in terms of circularly polarized
, the effect on the test particles would be basically the same, but rotated by 45 degrees, as shown in the second animation. Just as with light polarization, the polarizations of gravitational waves may also be expressed in terms of circularly polarized
waves. Gravitational waves are polarized because of the nature of their sources. The polarization of a wave actually depends on the angle from the source, as we will see in the next section.
Some more detailed examples:
More technically, the third time derivative of the quadrupole moment (or the l-th time derivative of the l-th multipole moment
) of an isolated system's stress-energy tensor
must be nonzero in order for it to emit gravitational radiation. This is analogous to the changing dipole moment of charge or current necessary for electromagnetic radiation.
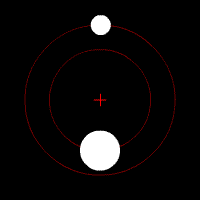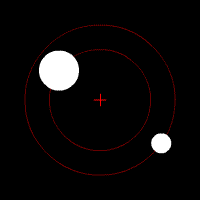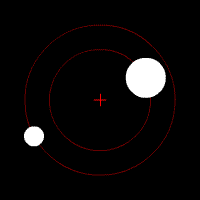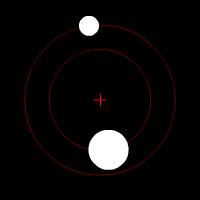
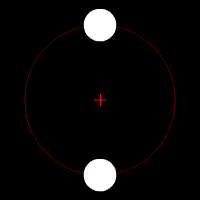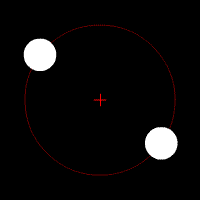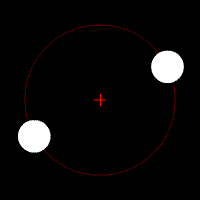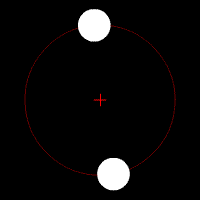
 Gravitational waves carry energy away from their sources and, in the case of orbiting bodies, this is associated with an inspiral or decrease in orbit. Imagine for example a simple system of two masses — such as the Earth-Sun system — moving slowly compared to the speed of light in circular orbits. Assume that these two masses orbit each other in a circular orbit in the
Gravitational waves carry energy away from their sources and, in the case of orbiting bodies, this is associated with an inspiral or decrease in orbit. Imagine for example a simple system of two masses — such as the Earth-Sun system — moving slowly compared to the speed of light in circular orbits. Assume that these two masses orbit each other in a circular orbit in the  -
-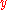 plane. To a good approximation, the masses follow simple Keplerian orbits
plane. To a good approximation, the masses follow simple Keplerian orbits
. However, such an orbit represents a changing quadrupole moment. That is, the system will give off gravitational waves.
Suppose that the two masses are and
and 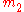 , and they are separated by a distance
, and they are separated by a distance  . The power given off (radiated) by this system is:
. The power given off (radiated) by this system is:
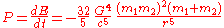 ,
,
where G is the gravitational constant
, c is the speed of light in vacuum and where the negative sign means that power is being given off by the system, rather than received. For a system like the Sun and Earth, is about 1.5 m and
is about 1.5 m and  and
and 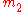 are about 2 and 6 kg respectively. In this case, the power is about 200 watts. This is truly tiny compared to the total electromagnetic radiation given off by the Sun (roughly 3.86 watts).
are about 2 and 6 kg respectively. In this case, the power is about 200 watts. This is truly tiny compared to the total electromagnetic radiation given off by the Sun (roughly 3.86 watts).
In theory, the loss of energy through gravitational radiation could eventually drop the Earth into the Sun. However, the total energy of the Earth orbiting the Sun (kinetic energy
plus gravitational potential energy) is about 1.14 joules of which only 200 joules per second is lost through gravitational radiation, leading to a decay in the orbit by about 1 meters per day or roughly the diameter of a proton
. At this rate, it would take the Earth approximately 1 times more than the current age of the Universe
to spiral onto the Sun. In only a few billion years, the Earth is predicted to be swallowed by the Sun in the red giant stage of its life.
A more dramatic example of radiated gravitational energy is represented by two solar mass neutron stars orbiting at a distance from each other of 1.89 m (only 0.63 light-second
s apart). [The Sun is 8 light minutes from the Earth.] Plugging their masses into the above equation shows that the gravitational radiation from them would be 1.38 watts, which is about 100 times more than the Sun's electromagnetic radiation.
 ,
,
where the variables are the same as in the previous equation.
The orbit decays at a rate proportional to the inverse third power of the radius. When the radius has shrunk to half its initial value, it is shrinking eight times faster than before. By Kepler's Third Law
, the new rotation rate at this point will be faster by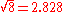 , or nearly three times the previous orbital frequency. As the radius decreases, the power lost to gravitational radiation increases even more. As can be seen from the previous equation, power radiated varies as the inverse fifth power of the radius, or 32 times more in this case.
, or nearly three times the previous orbital frequency. As the radius decreases, the power lost to gravitational radiation increases even more. As can be seen from the previous equation, power radiated varies as the inverse fifth power of the radius, or 32 times more in this case.
If we use the previous values for the Sun and the Earth, we find that the Earth's orbit shrinks by 1.1 meter per second. This is 3.5 m per year which is about 1/300 the diameter of a hydrogen atom
. The effect of gravitational radiation on the size of the Earth's orbit is negligible over the age of the universe. This is not true for closer orbits.
A more practical example is the orbit of a Sun-like star
around a heavy black hole
. Our Milky Way
has a 4 million solar-mass black hole at its center in Sagittarius A
. Such supermassive black holes are being found in the center of almost all galaxies
. For this example take a 2 million solar-mass black hole with a solar-mass star orbiting it at a radius of 1.89 m (63 light-seconds). The mass of the black hole will be 4 kg and its gravitational radius will be 6 m. The orbital period will be 1,000 seconds, or a little under 17 minutes. The solar-mass star will draw closer to the black hole by 7.4 meters per second or 7.4 km per orbit. A collision will not be long in coming.
Assume that a pair of solar-mass neutron stars are in circular orbits at a distance of 1.89 m (189,000 km). This is a little less than 1/7 the diameter of the Sun or 0.63 light-second
s. Their orbital period would be 1,000 seconds. Substituting the new mass and radius in the above formula gives a rate of orbit decrease of 3.7 m/s or 3.7 mm per orbit. This is 116 meters per year and is not negligible over cosmic time scales.
Suppose instead that these two neutron stars were orbiting at a distance of 1.89 m (1890 km). Their period would be 1 second and their orbital velocity would be about 1/50 of the speed of light. Their orbit would now shrink by 3.7 meters per orbit. A collision is imminent. A runaway loss of energy from the orbit results in an ever more rapid decrease in the distance between the stars. They will eventually merge to form a black hole and cease to radiate gravity waves. This is referred to as the inspiral
.
The above equation can not be applied directly for calculating the lifetime of the orbit, because the rate of change in radius depends on the radius itself, and is thus non-constant with time. The lifetime can be computed by integration of this equation (see next section).
The lifetime of an orbit is given by:
 ,
,
where r is the initial distance between the orbiting bodies. This equation can be derived by integrating the previous equation for the rate of radius decrease. It predicts the time for the radius of the orbit to shrink to zero. As the orbital speed becomes a significant fraction of the speed of light, this equation becomes inaccurate. It is useful for inspirals until the last few milliseconds before the merger of the objects.
Substituting the values for the mass of the Sun and Earth as well as the orbital radius gives a very large lifetime of 3.44 seconds or 1.09 years (which is approximately 1015 times larger than the age of the universe
). The actual figure would be slightly less than that. The Earth will break apart from tidal forces
if it orbits closer than a few radii from the sun. This would form a ring around the Sun and instantly stop the emission of gravity waves.
If we use a 2 million solar mass black hole with a solar mass star orbiting it at 1.89 meters, we get a lifetime of 6.50 seconds or 20.7 years.
Assume that a pair of solar mass neutron stars with a diameter of 10 kilometers are in circular orbits at a distance of 1.89 m (189,000 km). Their lifetime is 1.30 seconds or about 414,000 years. Their orbital period will be 1,000 seconds and it could be observed by LISA
if they were not too far away. A far greater number of white dwarf binaries exist with orbital periods in this range. White dwarf binaries have masses on the order of our Sun and diameters on the order of our Earth. They cannot get much closer together than 10,000 km before they will merge and cease to radiate gravitational waves. This results in the creation of either a neutron star or a black hole. Until then, their gravitational radiation will be comparable to that of a neutron star binary. LISA is the only gravitational wave experiment which is likely to succeed in detecting such types of binaries.
If the orbit of a neutron star binary has decayed to 1.89m (1890 km), its remaining lifetime is 130,000 seconds or about 36 hours. The orbital frequency will vary from 1 revolution per second at the start and 918 revolutions per second when the orbit has shrunk to 20 km at merger. The gravitational radiation emitted will be at twice the orbital frequency. Just before merger, the inspiral can be observed by LIGO if the binary is close enough. LIGO has only a few minutes to observe this merger out of a total orbital lifetime that may have been billions of years. Its chances of success are quite low despite the large number of such mergers occurring in the universe. No mergers have been seen in the few years that LIGO has been in operation. It is thought that a merger should be seen about once per decade of observing time.
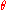 be the angle between the perpendicular to the plane of the orbit and the line of sight of the observer. Suppose that an observer is outside the system at a distance
be the angle between the perpendicular to the plane of the orbit and the line of sight of the observer. Suppose that an observer is outside the system at a distance  from its center of mass. If R is much greater than a wavelength, the two polarizations of the wave will be
from its center of mass. If R is much greater than a wavelength, the two polarizations of the wave will be
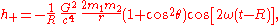
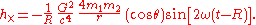
Here, we use the constant angular velocity
of a circular orbit in Newtonian physics:
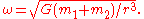
For example, if the observer is in the -
-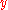 plane then
plane then  , and
, and 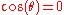 , so the
, so the 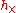 polarization is always zero. We also see that the frequency of the wave given off is twice the rotation frequency. If we put in numbers for the Earth-Sun system, we find:
polarization is always zero. We also see that the frequency of the wave given off is twice the rotation frequency. If we put in numbers for the Earth-Sun system, we find:
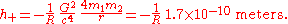
In this case, the minimum distance to find waves is R ≈ 1 light-year
, so typical amplitudes will be h ≈ 10−26. That is, a ring of particles would stretch or squeeze by just one part in 1026. This is well under the detectability limit of all conceivable detectors.
. The characteristics of their orbit can be deduced from the Doppler shifting of radio signals given off by the pulsar. Each of the stars has a mass about 1.4 times that of the Sun and the size of their orbit is about 1/75 of the Earth-Sun orbit. This means the distance between the two stars is just a few times larger than the diameter of our own Sun. The combination of greater masses and smaller separation means that the energy given off by the Hulse-Taylor binary will be far greater than the energy given off by the Earth-Sun system — roughly 1022 times as much.
The information about the orbit can be used to predict just how much energy (and angular momentum) should be given off in the form of gravitational waves. As the energy is carried off, the stars should draw closer to each other. This effect is called an inspiral
, and it can be observed in the pulsar's signals. The measurements on the Hulse-Taylor system have been carried out over more than 30 years. It has been shown that the gravitational radiation predicted by general relativity allows these observations to be matched within 0.2 percent. In 1993, Russell Hulse
and Joe Taylor were awarded the Nobel Prize in Physics
for this work, which was the first indirect evidence for gravitational waves. Unfortunately, the orbital lifetime of this binary system before merger is about 1.84 billion years. This is a substantial fraction of the age of the universe.
Inspirals are very important sources of gravitational waves. Any time two compact objects (white dwarfs, neutron stars, or black holes) are in close orbits, they send out intense gravitational waves. As they spiral closer to each other, these waves become more intense. At some point they should become so intense that direct detection by their effect on objects on Earth or in space is possible. This direct detection is the goal of several large scale experiments.
The only difficulty is that most systems like the Hulse-Taylor binary are so far away. The amplitude of waves given off by the Hulse-Taylor binary as seen on Earth would be roughly h ≈ 10−26. There are some sources, however, that astrophysicists expect to find with much larger amplitudes of h ≈ 10−20. At least eight other binary pulsars have been discovered.
 During the past century, astronomy
During the past century, astronomy
has been revolutionized by the use of new methods for observing the universe. Astronomical observations were originally made using visible light. Galileo Galilei
pioneered the use of telescopes to enhance these observations. However, visible light is only a small portion of the electromagnetic spectrum
, and not all objects in the distant universe shine strongly in this particular band. More useful information may be found, for example, in radio wavelengths. Using radio telescopes, astronomers have found pulsars, quasars, and other extreme objects which push the limits of our understanding of physics. Observations in the microwave
band have opened our eyes to the faint imprints
of the Big Bang
, a discovery Stephen Hawking
called the "greatest discovery of the century, if not all time". Similar advances in observations using gamma ray
s, x-ray
s, ultraviolet light, and infrared light have also brought new insights to astronomy. As each of these regions of the spectrum has opened, new discoveries have been made that could not have been made otherwise. Astronomers hope that the same holds true of gravitational waves.
Gravitational waves have two important and unique properties. First, there is no need for any type of matter to be present nearby in order for the waves to be generated by a binary system of uncharged black holes, which would emit no electromagnetic radiation. Second, gravitational waves can pass through any intervening matter without being scattered significantly. Whereas light from distant stars may be blocked out by interstellar dust, for example, gravitational waves will pass through essentially unimpeded. These two features allow gravitational waves to carry information about astronomical phenomena never before observed by humans.
The sources of gravitational waves described above are in the low-frequency end of the gravitational-wave spectrum (10−7 to 105 Hz). An astrophysical source at the high-frequency end of the gravitational-wave spectrum (above 105 Hz and probably 1010 Hz) generates relic gravitational waves that are theorized to be faint imprints of the Big Bang like the cosmic microwave background (see gravitational wave background
). At these high frequencies it is potentially possible that the sources may be "man made" that is, gravitational waves generated and detected in the laboratory.
, momentum
, and angular momentum
. By carrying these away from a source, waves are able to rob that source of its energy, linear or angular momentum. Gravitational waves perform the same function. Thus, for example, a binary system loses angular momentum as the two orbiting objects spiral towards each other—the angular momentum is radiated away by gravitational waves.
The waves can also carry off linear momentum, a possibility that has some interesting implications for astrophysics
. After two supermassive black holes coalesce, emission of linear momentum can produce a "kick" with amplitude as large as 4000 km/s. This is fast enough to eject the coalesced black hole completely from its host galaxy. Even if the kick is too small to eject the black hole completely, it can remove it temporarily from the nucleus of the galaxy, after which it will oscillate about the center, eventually coming to rest. A kicked black hole can also carry a star cluster with it, forming a hyper-compact stellar system. Or it may carry gas, allowing the recoiling black hole to appear temporarily as a "naked quasar
".
The quasar
SDSS J092712.65+294344.0
is believed to contain a recoiling supermassive black hole.
 term in the formulas for
term in the formulas for  above). Thus, even waves from extreme systems like merging binary black holes die out to very small amplitude by the time they reach the Earth. Astrophysicists expect that some gravitational waves passing the Earth may be as large as h ≈ 10−20, but generally no bigger.
above). Thus, even waves from extreme systems like merging binary black holes die out to very small amplitude by the time they reach the Earth. Astrophysicists expect that some gravitational waves passing the Earth may be as large as h ≈ 10−20, but generally no bigger.
A simple device to detect the expected wave motion is called a Weber bar
— a large, solid bar of metal isolated from outside vibrations. This type of instrument was the first type of gravitational wave detector. Strains in space due to an incident gravitational wave excite the bar's resonant frequency and could thus be amplified to detectable levels. Conceivably, a nearby supernova might be strong enough to be seen without resonant amplification. With this instrument, Joseph Weber
claimed to have detected daily signals of gravitational waves. His results, however, were contested in 1974 by physicists Richard Garwin
and David Douglass
. Modern forms of the Weber bar are still operated, cryogenically cooled, with superconducting quantum interference devices
to detect vibration. Weber bars are not sensitive enough to detect anything but extremely powerful gravitational waves.
MiniGRAIL
is a spherical gravitational wave antenna using this principle. It is based at Leiden University
, consisting of an exactingly machined 1150 kg sphere cryogenically cooled to 20 mK. The spherical configuration allows for equal sensitivity in all directions, and is somewhat experimentally simpler than larger linear devices requiring high vacuum. Events are detected by measuring deformation of the detector sphere
. MiniGRAIL is highly sensitive in the 2–4 kHz range, suitable for detecting gravitational waves from rotating neutron star instabilities or small black hole mergers.
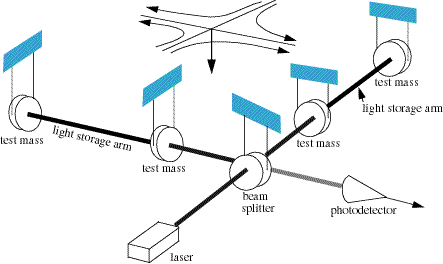 A more sensitive class of detector uses laser interferometry
A more sensitive class of detector uses laser interferometry
to measure gravitational-wave induced motion between separated 'free' masses. This allows the masses to be separated by large distances (increasing the signal size); a further advantage is that it is sensitive to a wide range of frequencies (not just those near a resonance as is the case for Weber bars). Ground-based interferometers are now operational. Currently, the most sensitive is LIGO
— the Laser Interferometer Gravitational Wave Observatory. LIGO has three detectors: one in Livingston, Louisiana
; the other two (in the same vacuum tubes) at the Hanford site
in Richland, Washington
. Each consists of two light storage arms which are 2 to 4 kilometers in length. These are at 90 degree angles to each other, with the light passing through 1m diameter vacuum tubes running the entire 4 kilometers. A passing gravitational wave will slightly stretch one arm as it shortens the other. This is precisely the motion to which an interferometer is most sensitive.
Even with such long arms, the strongest gravitational waves will only change the distance between the ends of the arms by at most roughly 10−18 meters. LIGO should be able to detect gravitational waves as small as h ≈ 5*10−20. Upgrades to LIGO and other detectors such as Virgo
, GEO 600
, and TAMA 300
should increase the sensitivity still further; the next generation of instruments (Advanced LIGO and Advanced Virgo) will be more than ten times more sensitive. Another highly sensitive interferometer (LCGT
) is currently in the design phase. A key point is that a tenfold increase in sensitivity (radius of 'reach') increases the volume of space accessible to the instrument by one thousand times. This increases the rate at which detectable signals should be seen from one per tens of years of observation, to tens per year.
Interferometric detectors are limited at high frequencies by shot noise
, which occurs because the lasers produce photons randomly; one analogy is to rainfall—the rate of rainfall, like the laser intensity, is measurable, but the raindrops, like photons, fall at random times, causing fluctuations around the average value. This leads to noise at the output of the detector, much like radio static. In addition, for sufficiently high laser power, the random momentum transferred to the test masses by the laser photons shakes the mirrors, masking signals at low frequencies. Thermal noise (e.g., Brownian motion
) is another limit to sensitivity. In addition to these 'stationary' (constant) noise sources, all ground-based detectors are also limited at low frequencies by seismic noise and other forms of environmental vibration, and other 'non-stationary' noise sources; creaks in mechanical structures, lightning or other large electrical disturbances, etc. may also create noise masking an event or may even imitate an event. All these must be taken into account and excluded by analysis before a detection may be considered a true gravitational wave event.
Space-based interferometers, such as LISA
and DECIGO, are also being developed. LISA's design calls for three test masses forming an equilateral triangle, with lasers from each spacecraft to each other spacecraft forming two independent interferometers. LISA is planned to occupy a solar orbit trailing the Earth, with each arm of the triangle being five million kilometers. This puts the detector in an excellent vacuum
far from Earth-based sources of noise, though it will still be susceptible to shot noise, as well as artifacts caused by cosmic ray
s and solar wind
.
There are currently two detectors focusing on detection at the higher end of the gravitational wave spectrum (10−7 to 105 Hz): one at University of Birmingham
, England, and the other at INFN
Genoa, Italy. A third is under development at Chongqing University
, China. The Birmingham detector measures changes in the polarization state of a microwave
beam circulating in a closed loop about one meter across. Two have been fabricated and they are currently expected to be sensitive to periodic spacetime strains of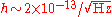 , given as an amplitude spectral density
, given as an amplitude spectral density
. The INFN Genoa detector is a resonant antenna consisting of two coupled spherical superconducting harmonic oscillators a few centimeters in diameter. The oscillators are designed to have (when uncoupled) almost equal resonant frequencies. The system is currently expected to have a sensitivity to periodic spacetime strains of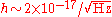 , with an expectation to reach a sensitivity of
, with an expectation to reach a sensitivity of 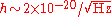 . The Chongqing University detector is planned to detect relic high-frequency gravitational waves with the predicted typical parameters ?g ~ 1010 Hz (10 GHz) and h ~ 10−30-10−31.
. The Chongqing University detector is planned to detect relic high-frequency gravitational waves with the predicted typical parameters ?g ~ 1010 Hz (10 GHz) and h ~ 10−30-10−31.
"—like a pure tone
in acoustics
. It would not change very much in amplitude or frequency.
The Einstein@Home
project is a distributed computing
project similar to SETI@home
intended to detect this type of simple gravitational wave. By taking data from LIGO and GEO, and sending it out in little pieces to thousands of volunteers for parallel analysis on their home computers, Einstein@Home can sift through the data far more quickly than would be possible otherwise.
— denoted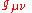 . The metric holds information regarding how distances are measured in the space under consideration. Because the propagation of gravitational waves through space and time change distances, we will need to use this to find the solution to the wave equation.
. The metric holds information regarding how distances are measured in the space under consideration. Because the propagation of gravitational waves through space and time change distances, we will need to use this to find the solution to the wave equation.
Spacetime curvature is also expressed with respect to a covariant derivative
, , in the form of the Einstein tensor
, in the form of the Einstein tensor
—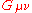 . This curvature is related to the stress-energy tensor
. This curvature is related to the stress-energy tensor
—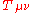 — by the key equation
— by the key equation
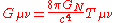 ,
,
where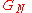 is Newton's gravitational constant
is Newton's gravitational constant
, and is the speed of light. We assume geometrized units, so
is the speed of light. We assume geometrized units, so  .
.
With some simple assumptions, Einstein's equations can be rewritten to show explicitly that they are wave equation
s. To begin with, we adopt some coordinate system, like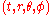 . We define the "flat-space metric"
. We define the "flat-space metric" 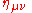 to be the quantity which — in this coordinate system — has the components we would expect for the flat space metric. For example, in these spherical coordinates, we have
to be the quantity which — in this coordinate system — has the components we would expect for the flat space metric. For example, in these spherical coordinates, we have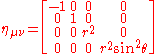 .
.
This flat-space metric has no physical significance; it is a purely mathematical device necessary for the analysis. Tensor indices are raised and lowered using this "flat-space metric".
Now, we can also think of the physical metric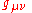 as a matrix
as a matrix
, and find its determinant
, . Finally, we define a quantity
. Finally, we define a quantity
 .
.
This is the crucial field, which will represent the radiation. It is possible (at least in an asymptotically flat spacetime
) to choose the coordinates in such a way that this quantity satisfies the "de Donder" gauge conditions (conditions on the coordinates):
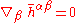 ,
,
where represents the flat-space derivative operator. These equations say that the divergence
represents the flat-space derivative operator. These equations say that the divergence
of the field is zero. The full, nonlinear Einstein equations can now be written as
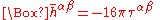 ,
,
where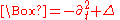 represents the flat-space d'Alembertian operator, and
represents the flat-space d'Alembertian operator, and 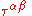 represents the stress-energy tensor plus quadratic terms involving
represents the stress-energy tensor plus quadratic terms involving 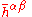 . This is just a wave equation for the field with a source, despite the fact that the source involves terms quadratic in the field itself. That is, it can be shown that solutions to this equation are waves traveling with velocity 1 in these coordinates.
. This is just a wave equation for the field with a source, despite the fact that the source involves terms quadratic in the field itself. That is, it can be shown that solutions to this equation are waves traveling with velocity 1 in these coordinates.
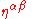 tensor. In this case, we can neglect terms quadratic in
tensor. In this case, we can neglect terms quadratic in 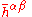 , which means that the
, which means that the 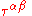 field reduces to the usual stress-energy tensor
field reduces to the usual stress-energy tensor 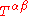 . That is, Einstein's equations become
. That is, Einstein's equations become
 .
.
If we are interested in the field far from a source, however, we can treat the source as a point source; everywhere else, the stress-energy tensor would be zero, so
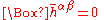 .
.
Now, this is the usual homogeneous wave equation — one for each component of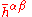 . Solutions to this equation are well known. For a wave moving away from a point source, the radiated part (meaning the part that dies off as
. Solutions to this equation are well known. For a wave moving away from a point source, the radiated part (meaning the part that dies off as 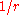 far from the source) can always be written in the form
far from the source) can always be written in the form 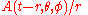 , where
, where 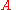 is just some function. It can be shown that — to a linear approximation — it is always possible to make the field traceless. Now, if we further assume that the source is positioned at
is just some function. It can be shown that — to a linear approximation — it is always possible to make the field traceless. Now, if we further assume that the source is positioned at  , the general solution to the wave equation in spherical coordinates is
, the general solution to the wave equation in spherical coordinates is
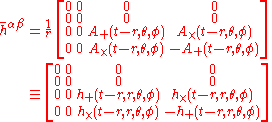
where we now see the origin of the two polarizations.
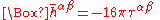 ,
,
we can write the solution in terms of the tensorial Green's function
for the d'Alembertian operator:
 .
.
Though it is possible to expand the Green's function in tensor spherical harmonics
, it is easier to simply use the form
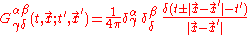 ,
,
where the positive and negative signs correspond to ingoing and outgoing solutions, respectively. Generally, we are interested in the outgoing solutions, so
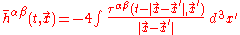 .
.
If the source is confined to a small region very far away, to an excellent approximation we have:
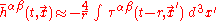 ,
,
where .
.
Now, because we will eventually only be interested in the spatial components of this equation (time components can be set to zero with a coordinate transformation), and we are integrating this quantity — presumably over a region of which there is no boundary — we can put this in a different form. Ignoring divergences with the help of Stokes' theorem
and an empty boundary, we can see that
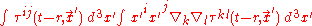 ,
,
Inserting this into the above equation, we arrive at
 ,
,
Finally, because we have chosen to work in coordinates for which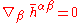 , we know that
, we know that 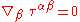 . With a few simple manipulations, we can use this to prove that
. With a few simple manipulations, we can use this to prove that
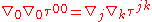 .
.
With this relation, the expression for the radiated field is
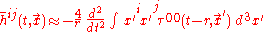 .
.
In the linear case,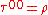 , the density of mass-energy.
, the density of mass-energy.
To a very good approximation, the density of a simple binary can be described by a pair of delta-functions, which eliminates the integral. Explicitly, if the masses of the two objects are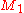 and
and 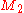 , and the positions are
, and the positions are 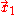 and
and 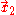 , then
, then
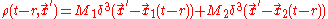 .
.
We can use this expression to do the integral above:
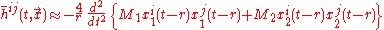 .
.
Using mass-centered coordinates, and assuming a circular binary, this is
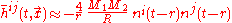 ,
,
where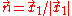 . Plugging in the known values of
. Plugging in the known values of 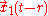 , we obtain the expressions given above for the radiation from a simple binary.
, we obtain the expressions given above for the radiation from a simple binary.
defined as: (1) the small fluctuations of curved spacetime which (2) have been separated from its source and propagate independently.
For instance, theory of superfluid vacuum
brings into question that the relativistic object possessing both of these properties may exist in Nature.
Indeed, according to the approach, the curved spacetime itself is the small collective excitation of the superfluid background, therefore,
the property (1) means that the gravitational wave would be in fact the "small fluctuation of the small fluctuation" which does not look like the physical concept
(as if somebody tried to introduce small fluctuations inside phonons, for instance).
As a result, it may be not just a coincidence that in general relativity
the gravitational field alone has no well-defined stress-energy tensor
,
only the pseudotensor
one.
Therefore, the property (2) cannot be completely justified in a theory with exact Lorentz symmetry which the general relativity is.
Though, SVT does not a priori forbid an existence of the non-localized wave
-like excitations of the superfluid background
which might be responsible for the astrophysical phenomena
which are currently being attributed to gravitational waves, such as the Hulse-Taylor binary. However, such excitations cannot be correctly described within the framework of a relativistic
theory.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, gravitational waves are theoretical ripples in the curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
which propagates as a wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
, traveling outward from the source. Predicted to exist by Albert Einstein
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
in 1916 on the basis of his theory of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, gravitational waves theoretically transport energy as gravitational radiation. Sources of gravitational waves could possibly include binary star
Binary star
A binary star is a star system consisting of two stars orbiting around their common center of mass. The brighter star is called the primary and the other is its companion star, comes, or secondary...
systems composed of white dwarfs, neutron stars, or black holes. The existence of gravitational waves is possibly a consequence of the Lorentz invariance of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
since it brings the concept of a limiting speed of propagation of the physical interactions with it. Gravitational waves cannot exist in the Newtonian theory of gravitation, since in it physical interactions propagate at infinite speed.
Although gravitational radiation has not been directly detected, there is indirect evidence for its existence. For example, the 1993 Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
was awarded for measurements of the Hulse-Taylor binary system which suggests gravitational waves are more than mathematical anomalies. Various gravitational wave detectors exist. However, they remain unsuccessful in detecting such phenomena.
Introduction
In Einstein's theory of general relativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
, gravity is treated as a phenomenon resulting in the curvature of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. This curvature is caused by the presence of massive objects. Roughly speaking, the more massive the object is, the greater the curvature it produces and hence the more intense the gravity. As massive objects move around in spacetime, the curvature changes to reflect the changed locations of those objects. In certain circumstances, objects that are accelerated
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
generate a disturbance in spacetime which spreads, as the metaphor goes, "like ripples on the surface of a pond", although perhaps a better analogy would be electromagnetic waves. This disturbance is known as gravitational radiation. Gravitational radiation is thought to travel through the Universe at the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, diminishing in strength but never stopping or slowing down.
As waves of gravitational radiation pass a distant observer, that observer will find spacetime distorted by the effects of strain. Distances between free objects will increase and decrease rhythmically as the wave passes. The magnitude of this effect will decrease the farther the observer is from the source. Binary neutron star
Neutron star
A neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
s are predicted to be a strong source of such waves owing to the acceleration of their enormous masses as they orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
each other and yet even those waves are expected to be very weak by the time they reach the Earth, resulting in strains of less than 1 part in 1020. Scientists are attempting to demonstrate the existence of these waves with ever more sensitive detectors. The current most sensitive measurement is about one part in 3 x 1022 (as of 2007) provided by the LIGO
LIGO
LIGO, which stands for the Laser Interferometer Gravitational-Wave Observatory, is a large-scale physics experiment aiming to directly detect gravitational waves. Cofounded in 1992 by Kip Thorne and Ronald Drever of Caltech and Rainer Weiss of MIT, LIGO is a joint project between scientists at MIT,...
detector. Sources this intense are not expected to last long so is merely a matter of luck if any are found. Another attempt, still under development, is Laser Interferometer Space Antenna
Laser Interferometer Space Antenna
The Laser Interferometer Space Antenna is a planned space mission to detect and accurately measure gravitational waves from astronomical sources. LISA was originally conceived as a joint effort between the United States space agency NASA and the European Space Agency...
, a joint effort of NASA and ESA.
Gravitational waves should penetrate regions of space that electromagnetic waves cannot. It is hypothesized that they will be able to provide observers on Earth with information about black holes and other mysterious objects in the distant Universe. Such systems cannot be observed with more traditional means such as optical telescope
Optical telescope
An optical telescope is a telescope which is used to gather and focus light mainly from the visible part of the electromagnetic spectrum for directly viewing a magnified image for making a photograph, or collecting data through electronic image sensors....
s and radio telescope
Radio telescope
A radio telescope is a form of directional radio antenna used in radio astronomy. The same types of antennas are also used in tracking and collecting data from satellites and space probes...
s. In particular, gravitational waves could be of interest to cosmologists as they offer a possible way of observing the very early universe. This is not possible with conventional astronomy, since before recombination
Recombination (cosmology)
In cosmology, recombination refers to the epoch at which charged electrons and protons first became bound to form electrically neutral hydrogen atoms.Note that the term recombination is a misnomer, considering that it represents the first time that electrically neutral hydrogen formed. After the...
the universe was opaque to electromagnetic radiation. Precise measurements of gravitational waves will also allow scientists to test the general theory of relativity more thoroughly.
In principle, gravitational waves could exist at any frequency. However, very low frequency waves would be impossible to detect and there is no credible source for detectable waves of very high frequency. Stephen W. Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
and Werner Israel
Werner Israel
Werner Israel, OC, FRSC, FRS is a Canadian physicist.Born in Berlin, Germany and raised in Cape Town, South Africa, he received his B.Sc. in 1951 and his M.Sc. in 1954 from the University of Cape Town. He received his Ph.D...
list different frequency bands for gravitational waves that could be plausibly detected, ranging from 10−7 Hz up to 1011 Hz.
Effects of a passing gravitational wave

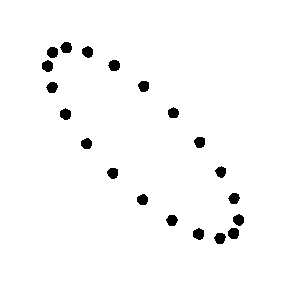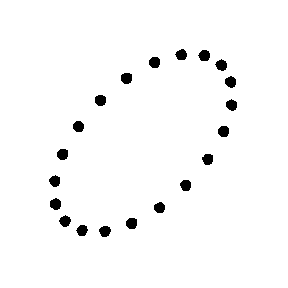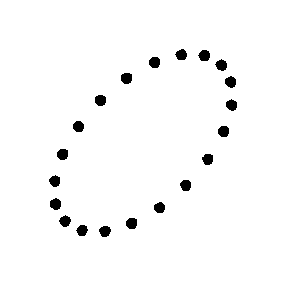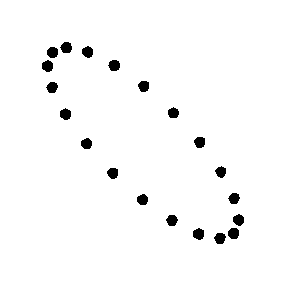
Cruciform
Cruciform means having the shape of a cross or Christian cross.- Cruciform architectural plan :This is a common description of Christian churches. In Early Christian, Byzantine and other Eastern Orthodox forms of church architecture this is more likely to mean a tetraconch plan, a Greek cross,...
" manner, as shown in the animations. The area enclosed by the test particles does not change and there is no motion along the direction of propagation.
The oscillations depicted here in the animation are of course immensely exaggerated for the purpose of discussion—in reality a gravitational wave has a very small amplitude (as formulated in linearized gravity
Linearized gravity
Linearized gravity is an approximation scheme in general relativity in which the nonlinear contributions from the spacetime metric are ignored, simplifying the study of many problems while still producing useful approximate results.-The method:...
). However they enable us to visualize the kind of oscillations associated with gravitational waves as produced for example by a pair of masses in a circular orbit
Circular orbit
A circular orbit is the orbit at a fixed distance around any point by an object rotating around a fixed axis.Below we consider a circular orbit in astrodynamics or celestial mechanics under standard assumptions...
. In this case the amplitude of the gravitational wave is a constant, but its plane of polarization changes or rotates at twice the orbital rate and so the time-varying gravitational wave size (or 'periodic spacetime strain') exhibits a variation as shown in the animation. If the orbit is elliptical then the gravitational wave's amplitude also varies with time according to an equation called the "quadrupole
Quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
".
Like other wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
s, there are a few useful characteristics describing a gravitational wave:
- Amplitude: Usually denoted
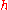 , this is the size of the wave — the fraction of stretching or squeezing in the animation. The amplitude shown here is roughly
, this is the size of the wave — the fraction of stretching or squeezing in the animation. The amplitude shown here is roughly 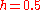 (or 50%). Gravitational waves passing through the Earth are many billions times weaker than this —
(or 50%). Gravitational waves passing through the Earth are many billions times weaker than this —  . Note that this is not the quantity which would be analogous to what is usually called the amplitude of an electromagnetic wave, which would be
. Note that this is not the quantity which would be analogous to what is usually called the amplitude of an electromagnetic wave, which would be 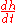 .
. - FrequencyFrequencyFrequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
: Usually denoted f, this is the frequency with which the wave oscillates (1 divided by the amount of time between two successive maximum stretches or squeezes) - WavelengthWavelengthIn physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
: Usually denoted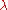 , this is the distance along the wave between points of maximum stretch or squeeze.
, this is the distance along the wave between points of maximum stretch or squeeze. - SpeedSpeedIn kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...
: This is the speed at which a point on the wave (for example, a point of maximum stretch or squeeze) travels. For gravitational waves with small amplitudes, this is equal to the speed of lightSpeed of lightThe speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
, .
.
The speed, wavelength, and frequency of a gravitational wave are related by the equation c = λ f, just like the equation for a light wave. For example, the animations shown here oscillate roughly once every two seconds. This would correspond to a frequency of 0.5 Hz, and a wavelength of about 600,000 km, or 47 times the diameter of the Earth.
In the example just discussed, we actually assume something special about the wave. We have assumed that the wave is linearly polarized
Linear polarization
In electrodynamics, linear polarization or plane polarization of electromagnetic radiation is a confinement of the electric field vector or magnetic field vector to a given plane along the direction of propagation...
, with a "plus" polarization, written
 . Polarization of a gravitational wave is just like polarization of a light wave except that the polarizations of a gravitational wave are at 45 degrees, as opposed to 90 degrees. In particular, if we had a "cross"-polarized gravitational wave,
. Polarization of a gravitational wave is just like polarization of a light wave except that the polarizations of a gravitational wave are at 45 degrees, as opposed to 90 degrees. In particular, if we had a "cross"-polarized gravitational wave,  , the effect on the test particles would be basically the same, but rotated by 45 degrees, as shown in the second animation. Just as with light polarization, the polarizations of gravitational waves may also be expressed in terms of circularly polarized
, the effect on the test particles would be basically the same, but rotated by 45 degrees, as shown in the second animation. Just as with light polarization, the polarizations of gravitational waves may also be expressed in terms of circularly polarizedCircular polarization
In electrodynamics, circular polarization of an electromagnetic wave is a polarization in which the electric field of the passing wave does not change strength but only changes direction in a rotary type manner....
waves. Gravitational waves are polarized because of the nature of their sources. The polarization of a wave actually depends on the angle from the source, as we will see in the next section.
Sources of gravitational waves
In general terms, gravitational waves are radiated by objects whose motion involves acceleration, provided that the motion is not perfectly spherically symmetric (like an expanding or contracting sphere) or cylindrically symmetric (like a spinning disk or sphere). A simple example of this principle is provided by the spinning dumbbell. If the dumbbell spins like wheels on an axle, it will not radiate gravitational waves; if it tumbles end over end like two planets orbiting each other, it will radiate gravitational waves. The heavier the dumbbell, and the faster it tumbles, the greater is the gravitational radiation it will give off. If we imagine an extreme case in which the two weights of the dumbbell are massive stars like neutron stars or black holes, orbiting each other quickly, then significant amounts of gravitational radiation would be given off.Some more detailed examples:
- Two objects orbiting each other in a quasi-Keplerian planar orbit (basically, as a planet would orbit the Sun) will radiate.
- A spinning non-axisymmetric planetoid — say with a large bump or dimple on the equator — will radiate.
- A supernovaSupernovaA supernova is a stellar explosion that is more energetic than a nova. It is pronounced with the plural supernovae or supernovas. Supernovae are extremely luminous and cause a burst of radiation that often briefly outshines an entire galaxy, before fading from view over several weeks or months...
will radiate except in the unlikely event that the explosion is perfectly symmetric. - An isolated non-spinning solid object moving at a constant speed will not radiate. This can be regarded as a consequence of the principle of conservation of linear momentum.
- A spinning disk will not radiate. This can be regarded as a consequence of the principle of conservation of angular momentum. However, it will show gravitomagneticGravitomagnetismGravitomagnetism , refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test...
effects. - A spherically pulsating spherical star (non-zero monopole moment or massMassMass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
, but zero quadrupole moment) will not radiate, in agreement with Birkhoff's theoremBirkhoff's theorem (relativity)In general relativity, Birkhoff's theorem states that any spherically symmetric solution of the vacuum field equations must be static and asymptotically flat. This means that the exterior solution must be given by the Schwarzschild metric....
.
More technically, the third time derivative of the quadrupole moment (or the l-th time derivative of the l-th multipole moment
Multipole expansion
A multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
) of an isolated system's stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
must be nonzero in order for it to emit gravitational radiation. This is analogous to the changing dipole moment of charge or current necessary for electromagnetic radiation.
Power radiated by orbiting bodies



 -
-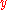 plane. To a good approximation, the masses follow simple Keplerian orbits
plane. To a good approximation, the masses follow simple Keplerian orbitsPlanetary orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
. However, such an orbit represents a changing quadrupole moment. That is, the system will give off gravitational waves.
Suppose that the two masses are
 and
and 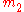 , and they are separated by a distance
, and they are separated by a distance  . The power given off (radiated) by this system is:
. The power given off (radiated) by this system is: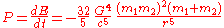 ,
,where G is the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, c is the speed of light in vacuum and where the negative sign means that power is being given off by the system, rather than received. For a system like the Sun and Earth,
 is about 1.5 m and
is about 1.5 m and  and
and 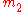 are about 2 and 6 kg respectively. In this case, the power is about 200 watts. This is truly tiny compared to the total electromagnetic radiation given off by the Sun (roughly 3.86 watts).
are about 2 and 6 kg respectively. In this case, the power is about 200 watts. This is truly tiny compared to the total electromagnetic radiation given off by the Sun (roughly 3.86 watts).In theory, the loss of energy through gravitational radiation could eventually drop the Earth into the Sun. However, the total energy of the Earth orbiting the Sun (kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
plus gravitational potential energy) is about 1.14 joules of which only 200 joules per second is lost through gravitational radiation, leading to a decay in the orbit by about 1 meters per day or roughly the diameter of a proton
Proton
The proton is a subatomic particle with the symbol or and a positive electric charge of 1 elementary charge. One or more protons are present in the nucleus of each atom, along with neutrons. The number of protons in each atom is its atomic number....
. At this rate, it would take the Earth approximately 1 times more than the current age of the Universe
Age of the universe
The age of the universe is the time elapsed since the Big Bang posited by the most widely accepted scientific model of cosmology. The best current estimate of the age of the universe is 13.75 ± 0.13 billion years within the Lambda-CDM concordance model...
to spiral onto the Sun. In only a few billion years, the Earth is predicted to be swallowed by the Sun in the red giant stage of its life.
A more dramatic example of radiated gravitational energy is represented by two solar mass neutron stars orbiting at a distance from each other of 1.89 m (only 0.63 light-second
Light-second
A light-second is a unit of length useful in astronomy, telecommunications and relativistic physics. It is defined as the distance that light travels in free space in one second, and is equal to exactly 299,792,458 metres...
s apart). [The Sun is 8 light minutes from the Earth.] Plugging their masses into the above equation shows that the gravitational radiation from them would be 1.38 watts, which is about 100 times more than the Sun's electromagnetic radiation.
Orbital decay from gravitational radiation
Gravitational radiation robs the orbiting bodies of energy. It first circularizes their orbits and then gradually shrinks their radius. As the energy of the orbit is reduced, the distance between the bodies decreases, and they rotate more rapidly. The overall angular momentum is reduced however. This reduction corresponds to the angular momentum carried off by gravitational radiation. The rate of decrease of distance between the bodies versus time is given by: ,
,where the variables are the same as in the previous equation.
The orbit decays at a rate proportional to the inverse third power of the radius. When the radius has shrunk to half its initial value, it is shrinking eight times faster than before. By Kepler's Third Law
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
, the new rotation rate at this point will be faster by
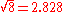 , or nearly three times the previous orbital frequency. As the radius decreases, the power lost to gravitational radiation increases even more. As can be seen from the previous equation, power radiated varies as the inverse fifth power of the radius, or 32 times more in this case.
, or nearly three times the previous orbital frequency. As the radius decreases, the power lost to gravitational radiation increases even more. As can be seen from the previous equation, power radiated varies as the inverse fifth power of the radius, or 32 times more in this case.If we use the previous values for the Sun and the Earth, we find that the Earth's orbit shrinks by 1.1 meter per second. This is 3.5 m per year which is about 1/300 the diameter of a hydrogen atom
Hydrogen atom
A hydrogen atom is an atom of the chemical element hydrogen. The electrically neutral atom contains a single positively-charged proton and a single negatively-charged electron bound to the nucleus by the Coulomb force...
. The effect of gravitational radiation on the size of the Earth's orbit is negligible over the age of the universe. This is not true for closer orbits.
A more practical example is the orbit of a Sun-like star
Solar analog
Solar-type, solar analog, and solar twin stars are those stars that are particularly similar to the Sun. The classification is a hierarchy with solar twin being most like the Sun followed by solar analog and then solar-type...
around a heavy black hole
Black hole
A black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
. Our Milky Way
Milky Way
The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
has a 4 million solar-mass black hole at its center in Sagittarius A
Sagittarius A
Sagittarius A is a complex radio source at the center of our galaxy, the Milky Way. It is located in the sky in the Sagittarius constellation...
. Such supermassive black holes are being found in the center of almost all galaxies
Galaxy
A galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a...
. For this example take a 2 million solar-mass black hole with a solar-mass star orbiting it at a radius of 1.89 m (63 light-seconds). The mass of the black hole will be 4 kg and its gravitational radius will be 6 m. The orbital period will be 1,000 seconds, or a little under 17 minutes. The solar-mass star will draw closer to the black hole by 7.4 meters per second or 7.4 km per orbit. A collision will not be long in coming.
Assume that a pair of solar-mass neutron stars are in circular orbits at a distance of 1.89 m (189,000 km). This is a little less than 1/7 the diameter of the Sun or 0.63 light-second
Light-second
A light-second is a unit of length useful in astronomy, telecommunications and relativistic physics. It is defined as the distance that light travels in free space in one second, and is equal to exactly 299,792,458 metres...
s. Their orbital period would be 1,000 seconds. Substituting the new mass and radius in the above formula gives a rate of orbit decrease of 3.7 m/s or 3.7 mm per orbit. This is 116 meters per year and is not negligible over cosmic time scales.
Suppose instead that these two neutron stars were orbiting at a distance of 1.89 m (1890 km). Their period would be 1 second and their orbital velocity would be about 1/50 of the speed of light. Their orbit would now shrink by 3.7 meters per orbit. A collision is imminent. A runaway loss of energy from the orbit results in an ever more rapid decrease in the distance between the stars. They will eventually merge to form a black hole and cease to radiate gravity waves. This is referred to as the inspiral
Inspiral
Inspiral refers to the path of binary stars which are losing energy and approaching each other. Several things can cause the loss of energy including tidal forces, mass transfer, and gravitational radiation. The stars describe the path of a spiral as they approach each other. This sometimes...
.
The above equation can not be applied directly for calculating the lifetime of the orbit, because the rate of change in radius depends on the radius itself, and is thus non-constant with time. The lifetime can be computed by integration of this equation (see next section).
Orbital lifetime limits from gravitational radiation
Orbital lifetime is one of the most important properties of gravitational radiation sources. It determines the average number of binary stars in the universe that are close enough to be detected. Short lifetime binaries are strong sources of gravitational radiation but are few in number. Long lifetime binaries are more plentiful but they are weak sources of gravity waves. LIGO is most sensitive in the frequency band where two neutron stars are about to merge. This time frame is only a few seconds. It takes luck for the detector to see this blink in time out of a million year orbital lifetime. It is predicted that such a merger will only be seen once per decade or so.The lifetime of an orbit is given by:
 ,
,where r is the initial distance between the orbiting bodies. This equation can be derived by integrating the previous equation for the rate of radius decrease. It predicts the time for the radius of the orbit to shrink to zero. As the orbital speed becomes a significant fraction of the speed of light, this equation becomes inaccurate. It is useful for inspirals until the last few milliseconds before the merger of the objects.
Substituting the values for the mass of the Sun and Earth as well as the orbital radius gives a very large lifetime of 3.44 seconds or 1.09 years (which is approximately 1015 times larger than the age of the universe
Age of the universe
The age of the universe is the time elapsed since the Big Bang posited by the most widely accepted scientific model of cosmology. The best current estimate of the age of the universe is 13.75 ± 0.13 billion years within the Lambda-CDM concordance model...
). The actual figure would be slightly less than that. The Earth will break apart from tidal forces
Roche limit
The Roche limit , sometimes referred to as the Roche radius, is the distance within which a celestial body, held together only by its own gravity, will disintegrate due to a second celestial body's tidal forces exceeding the first body's gravitational self-attraction...
if it orbits closer than a few radii from the sun. This would form a ring around the Sun and instantly stop the emission of gravity waves.
If we use a 2 million solar mass black hole with a solar mass star orbiting it at 1.89 meters, we get a lifetime of 6.50 seconds or 20.7 years.
Assume that a pair of solar mass neutron stars with a diameter of 10 kilometers are in circular orbits at a distance of 1.89 m (189,000 km). Their lifetime is 1.30 seconds or about 414,000 years. Their orbital period will be 1,000 seconds and it could be observed by LISA
Laser Interferometer Space Antenna
The Laser Interferometer Space Antenna is a planned space mission to detect and accurately measure gravitational waves from astronomical sources. LISA was originally conceived as a joint effort between the United States space agency NASA and the European Space Agency...
if they were not too far away. A far greater number of white dwarf binaries exist with orbital periods in this range. White dwarf binaries have masses on the order of our Sun and diameters on the order of our Earth. They cannot get much closer together than 10,000 km before they will merge and cease to radiate gravitational waves. This results in the creation of either a neutron star or a black hole. Until then, their gravitational radiation will be comparable to that of a neutron star binary. LISA is the only gravitational wave experiment which is likely to succeed in detecting such types of binaries.
If the orbit of a neutron star binary has decayed to 1.89m (1890 km), its remaining lifetime is 130,000 seconds or about 36 hours. The orbital frequency will vary from 1 revolution per second at the start and 918 revolutions per second when the orbit has shrunk to 20 km at merger. The gravitational radiation emitted will be at twice the orbital frequency. Just before merger, the inspiral can be observed by LIGO if the binary is close enough. LIGO has only a few minutes to observe this merger out of a total orbital lifetime that may have been billions of years. Its chances of success are quite low despite the large number of such mergers occurring in the universe. No mergers have been seen in the few years that LIGO has been in operation. It is thought that a merger should be seen about once per decade of observing time.
Wave amplitudes from the Earth-Sun system
We can also think in terms of the amplitude of the wave from a system in circular orbits. Let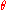 be the angle between the perpendicular to the plane of the orbit and the line of sight of the observer. Suppose that an observer is outside the system at a distance
be the angle between the perpendicular to the plane of the orbit and the line of sight of the observer. Suppose that an observer is outside the system at a distance  from its center of mass. If R is much greater than a wavelength, the two polarizations of the wave will be
from its center of mass. If R is much greater than a wavelength, the two polarizations of the wave will be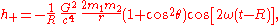
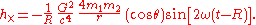
Here, we use the constant angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of a circular orbit in Newtonian physics:
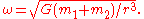
For example, if the observer is in the
 -
-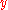 plane then
plane then  , and
, and 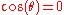 , so the
, so the 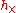 polarization is always zero. We also see that the frequency of the wave given off is twice the rotation frequency. If we put in numbers for the Earth-Sun system, we find:
polarization is always zero. We also see that the frequency of the wave given off is twice the rotation frequency. If we put in numbers for the Earth-Sun system, we find: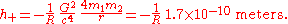
In this case, the minimum distance to find waves is R ≈ 1 light-year
Light-year
A light-year, also light year or lightyear is a unit of length, equal to just under 10 trillion kilometres...
, so typical amplitudes will be h ≈ 10−26. That is, a ring of particles would stretch or squeeze by just one part in 1026. This is well under the detectability limit of all conceivable detectors.
Radiation from other sources
Although the waves from the Earth-Sun system are minuscule, astronomers can point to other sources for which the radiation should be substantial. One important example is the Hulse-Taylor binary — a pair of stars, one of which is a pulsarBinary pulsar
A binary pulsar is a pulsar with a binary companion, often a white dwarf or neutron star. Binary pulsars are one of the few objects which allow physicists to test general relativity in the case of a strong gravitational field...
. The characteristics of their orbit can be deduced from the Doppler shifting of radio signals given off by the pulsar. Each of the stars has a mass about 1.4 times that of the Sun and the size of their orbit is about 1/75 of the Earth-Sun orbit. This means the distance between the two stars is just a few times larger than the diameter of our own Sun. The combination of greater masses and smaller separation means that the energy given off by the Hulse-Taylor binary will be far greater than the energy given off by the Earth-Sun system — roughly 1022 times as much.
The information about the orbit can be used to predict just how much energy (and angular momentum) should be given off in the form of gravitational waves. As the energy is carried off, the stars should draw closer to each other. This effect is called an inspiral
Inspiral
Inspiral refers to the path of binary stars which are losing energy and approaching each other. Several things can cause the loss of energy including tidal forces, mass transfer, and gravitational radiation. The stars describe the path of a spiral as they approach each other. This sometimes...
, and it can be observed in the pulsar's signals. The measurements on the Hulse-Taylor system have been carried out over more than 30 years. It has been shown that the gravitational radiation predicted by general relativity allows these observations to be matched within 0.2 percent. In 1993, Russell Hulse
Russell Alan Hulse
Russell Alan Hulse is an American physicist and winner of the Nobel Prize in Physics, shared with his thesis advisor Joseph Hooton Taylor Jr., "for the discovery of a new type of pulsar, a discovery that has opened up new possibilities for the study of gravitation"...
and Joe Taylor were awarded the Nobel Prize in Physics
Nobel Prize in Physics
The Nobel Prize in Physics is awarded once a year by the Royal Swedish Academy of Sciences. It is one of the five Nobel Prizes established by the will of Alfred Nobel in 1895 and awarded since 1901; the others are the Nobel Prize in Chemistry, Nobel Prize in Literature, Nobel Peace Prize, and...
for this work, which was the first indirect evidence for gravitational waves. Unfortunately, the orbital lifetime of this binary system before merger is about 1.84 billion years. This is a substantial fraction of the age of the universe.
Inspirals are very important sources of gravitational waves. Any time two compact objects (white dwarfs, neutron stars, or black holes) are in close orbits, they send out intense gravitational waves. As they spiral closer to each other, these waves become more intense. At some point they should become so intense that direct detection by their effect on objects on Earth or in space is possible. This direct detection is the goal of several large scale experiments.
The only difficulty is that most systems like the Hulse-Taylor binary are so far away. The amplitude of waves given off by the Hulse-Taylor binary as seen on Earth would be roughly h ≈ 10−26. There are some sources, however, that astrophysicists expect to find with much larger amplitudes of h ≈ 10−20. At least eight other binary pulsars have been discovered.
Astrophysics and gravitational waves

Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
has been revolutionized by the use of new methods for observing the universe. Astronomical observations were originally made using visible light. Galileo Galilei
Galileo Galilei
Galileo Galilei , was an Italian physicist, mathematician, astronomer, and philosopher who played a major role in the Scientific Revolution. His achievements include improvements to the telescope and consequent astronomical observations and support for Copernicanism...
pioneered the use of telescopes to enhance these observations. However, visible light is only a small portion of the electromagnetic spectrum
Electromagnetic spectrum
The electromagnetic spectrum is the range of all possible frequencies of electromagnetic radiation. The "electromagnetic spectrum" of an object is the characteristic distribution of electromagnetic radiation emitted or absorbed by that particular object....
, and not all objects in the distant universe shine strongly in this particular band. More useful information may be found, for example, in radio wavelengths. Using radio telescopes, astronomers have found pulsars, quasars, and other extreme objects which push the limits of our understanding of physics. Observations in the microwave
Microwave
Microwaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
band have opened our eyes to the faint imprints
Cosmic microwave background radiation
In cosmology, cosmic microwave background radiation is thermal radiation filling the observable universe almost uniformly....
of the Big Bang
Big Bang
The Big Bang theory is the prevailing cosmological model that explains the early development of the Universe. According to the Big Bang theory, the Universe was once in an extremely hot and dense state which expanded rapidly. This rapid expansion caused the young Universe to cool and resulted in...
, a discovery Stephen Hawking
Stephen Hawking
Stephen William Hawking, CH, CBE, FRS, FRSA is an English theoretical physicist and cosmologist, whose scientific books and public appearances have made him an academic celebrity...
called the "greatest discovery of the century, if not all time". Similar advances in observations using gamma ray
Gamma ray
Gamma radiation, also known as gamma rays or hyphenated as gamma-rays and denoted as γ, is electromagnetic radiation of high frequency . Gamma rays are usually naturally produced on Earth by decay of high energy states in atomic nuclei...
s, x-ray
X-ray
X-radiation is a form of electromagnetic radiation. X-rays have a wavelength in the range of 0.01 to 10 nanometers, corresponding to frequencies in the range 30 petahertz to 30 exahertz and energies in the range 120 eV to 120 keV. They are shorter in wavelength than UV rays and longer than gamma...
s, ultraviolet light, and infrared light have also brought new insights to astronomy. As each of these regions of the spectrum has opened, new discoveries have been made that could not have been made otherwise. Astronomers hope that the same holds true of gravitational waves.
Gravitational waves have two important and unique properties. First, there is no need for any type of matter to be present nearby in order for the waves to be generated by a binary system of uncharged black holes, which would emit no electromagnetic radiation. Second, gravitational waves can pass through any intervening matter without being scattered significantly. Whereas light from distant stars may be blocked out by interstellar dust, for example, gravitational waves will pass through essentially unimpeded. These two features allow gravitational waves to carry information about astronomical phenomena never before observed by humans.
The sources of gravitational waves described above are in the low-frequency end of the gravitational-wave spectrum (10−7 to 105 Hz). An astrophysical source at the high-frequency end of the gravitational-wave spectrum (above 105 Hz and probably 1010 Hz) generates relic gravitational waves that are theorized to be faint imprints of the Big Bang like the cosmic microwave background (see gravitational wave background
Gravitational wave background
A possible target of gravitational wave detection experiments is a stochastic background of gravitational waves. This background is known as the gravitational wave background or the stochastic background...
). At these high frequencies it is potentially possible that the sources may be "man made" that is, gravitational waves generated and detected in the laboratory.
Energy, momentum, and angular momentum carried by gravitational waves
Waves familiar from other areas of physics such as water waves, sound waves, and electromagnetic waves are able to carry energyEnergy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
, and angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
. By carrying these away from a source, waves are able to rob that source of its energy, linear or angular momentum. Gravitational waves perform the same function. Thus, for example, a binary system loses angular momentum as the two orbiting objects spiral towards each other—the angular momentum is radiated away by gravitational waves.
The waves can also carry off linear momentum, a possibility that has some interesting implications for astrophysics
Astrophysics
Astrophysics is the branch of astronomy that deals with the physics of the universe, including the physical properties of celestial objects, as well as their interactions and behavior...
. After two supermassive black holes coalesce, emission of linear momentum can produce a "kick" with amplitude as large as 4000 km/s. This is fast enough to eject the coalesced black hole completely from its host galaxy. Even if the kick is too small to eject the black hole completely, it can remove it temporarily from the nucleus of the galaxy, after which it will oscillate about the center, eventually coming to rest. A kicked black hole can also carry a star cluster with it, forming a hyper-compact stellar system. Or it may carry gas, allowing the recoiling black hole to appear temporarily as a "naked quasar
HE0450-2958
HE0450-2958 is an unusual quasar. It has been called the "naked quasar" and the "quasar without a home" because it appears to lack a host galaxy. It is estimated to lie approximately one billion parsecs away.-History:...
".
The quasar
Quasar
A quasi-stellar radio source is a very energetic and distant active galactic nucleus. Quasars are extremely luminous and were first identified as being high redshift sources of electromagnetic energy, including radio waves and visible light, that were point-like, similar to stars, rather than...
SDSS J092712.65+294344.0
SDSS J0927+2943
SDSS J0927+2943 is an unusual quasar. It exhibits two sets of optical emission lines with different redshifts. The origin of the two emission line systems is believed to be a gravitational wave recoil event: the ejection of a supermassive black hole from the center of the host galaxy...
is believed to contain a recoiling supermassive black hole.
Gravitational wave detectors
Though the Hulse-Taylor observations were very important, they give only indirect evidence for gravitational waves. A more conclusive observation would be a direct measurement of the effect of a passing gravitational wave, which could also provide more information about the system which generated it. Any such direct detection is complicated by the extraordinarily small effect the waves would produce on a detector. The amplitude of a spherical wave will fall off as the inverse of the distance from the source (the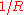 term in the formulas for
term in the formulas for 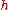 above). Thus, even waves from extreme systems like merging binary black holes die out to very small amplitude by the time they reach the Earth. Astrophysicists expect that some gravitational waves passing the Earth may be as large as h ≈ 10−20, but generally no bigger.
above). Thus, even waves from extreme systems like merging binary black holes die out to very small amplitude by the time they reach the Earth. Astrophysicists expect that some gravitational waves passing the Earth may be as large as h ≈ 10−20, but generally no bigger.A simple device to detect the expected wave motion is called a Weber bar
Weber bar
A Weber bar is a device used in the detection of gravitational waves first devised and constructed by physicist Joseph Weber at the University of Maryland...
— a large, solid bar of metal isolated from outside vibrations. This type of instrument was the first type of gravitational wave detector. Strains in space due to an incident gravitational wave excite the bar's resonant frequency and could thus be amplified to detectable levels. Conceivably, a nearby supernova might be strong enough to be seen without resonant amplification. With this instrument, Joseph Weber
Joseph Weber
Joseph Weber was an American physicist. He gave the earliest public lecture on the principles behind the laser and the maser and developed the first gravitational wave detectors .-Early education:...
claimed to have detected daily signals of gravitational waves. His results, however, were contested in 1974 by physicists Richard Garwin
Richard Garwin
Richard Lawrence Garwin , is an American physicist. He received his bachelor's degree from the Case Institute of Technology in 1947 and obtained his Doctor of Philosophy from the University of Chicago in 1949, where he worked in the lab of Enrico Fermi.Garwin is IBM Fellow Emeritus at the Thomas J...
and David Douglass
David Douglass
David H. Douglass is an American physicist at the University of Rochester. Prof. Douglass received his B.S. in Physics from the University of Maine and his Ph.D. in Physics from the Massachusetts Institute of Technology. After positions at MIT Lincoln Laboratories and MIT, he was appointed...
. Modern forms of the Weber bar are still operated, cryogenically cooled, with superconducting quantum interference devices
SQUID
A SQUID is a very sensitive magnetometer used to measure extremely weak magnetic fields, based on superconducting loops containing Josephson junctions....
to detect vibration. Weber bars are not sensitive enough to detect anything but extremely powerful gravitational waves.
MiniGRAIL
MiniGrail
MiniGRAIL is an instrument that is designed to detect gravitational waves. The MiniGRAIL is the first such detector to use a spherical design. It is located at Leiden University in the Netherlands. The project is being managed by the Kamerlingh Onnes Laboratory...
is a spherical gravitational wave antenna using this principle. It is based at Leiden University
Leiden University
Leiden University , located in the city of Leiden, is the oldest university in the Netherlands. The university was founded in 1575 by William, Prince of Orange, leader of the Dutch Revolt in the Eighty Years' War. The royal Dutch House of Orange-Nassau and Leiden University still have a close...
, consisting of an exactingly machined 1150 kg sphere cryogenically cooled to 20 mK. The spherical configuration allows for equal sensitivity in all directions, and is somewhat experimentally simpler than larger linear devices requiring high vacuum. Events are detected by measuring deformation of the detector sphere
Multipole moments
In mathematics, especially as applied to physics, multipole moments are the coefficients of a series expansion of a potential due to continuous or discrete sources . A multipole moment usually involves powers of the distance to the origin, as well as some angular dependence...
. MiniGRAIL is highly sensitive in the 2–4 kHz range, suitable for detecting gravitational waves from rotating neutron star instabilities or small black hole mergers.

Interferometry
Interferometry refers to a family of techniques in which electromagnetic waves are superimposed in order to extract information about the waves. An instrument used to interfere waves is called an interferometer. Interferometry is an important investigative technique in the fields of astronomy,...
to measure gravitational-wave induced motion between separated 'free' masses. This allows the masses to be separated by large distances (increasing the signal size); a further advantage is that it is sensitive to a wide range of frequencies (not just those near a resonance as is the case for Weber bars). Ground-based interferometers are now operational. Currently, the most sensitive is LIGO
LIGO
LIGO, which stands for the Laser Interferometer Gravitational-Wave Observatory, is a large-scale physics experiment aiming to directly detect gravitational waves. Cofounded in 1992 by Kip Thorne and Ronald Drever of Caltech and Rainer Weiss of MIT, LIGO is a joint project between scientists at MIT,...
— the Laser Interferometer Gravitational Wave Observatory. LIGO has three detectors: one in Livingston, Louisiana
Livingston, Louisiana
Livingston is a town in and the parish seat of Livingston Parish, Louisiana, United States. The population was 1,342 at the 2000 census. It is part of the Baton Rouge Metropolitan Statistical Area....
; the other two (in the same vacuum tubes) at the Hanford site
Hanford Site
The Hanford Site is a mostly decommissioned nuclear production complex on the Columbia River in the U.S. state of Washington, operated by the United States federal government. The site has been known by many names, including Hanford Works, Hanford Engineer Works or HEW, Hanford Nuclear Reservation...
in Richland, Washington
Richland, Washington
Richland is a city in Benton County in the southeastern part of the U.S. state of Washington, at the confluence of the Yakima and the Columbia Rivers. As of the 2010 census, the city population was 48,058. April 1, 2011 estimates from the Washington State Office of Financial Management put the...
. Each consists of two light storage arms which are 2 to 4 kilometers in length. These are at 90 degree angles to each other, with the light passing through 1m diameter vacuum tubes running the entire 4 kilometers. A passing gravitational wave will slightly stretch one arm as it shortens the other. This is precisely the motion to which an interferometer is most sensitive.
Even with such long arms, the strongest gravitational waves will only change the distance between the ends of the arms by at most roughly 10−18 meters. LIGO should be able to detect gravitational waves as small as h ≈ 5*10−20. Upgrades to LIGO and other detectors such as Virgo
Virgo interferometer
The Virgo is a gravitational wave detector in Italy, which commenced operations in 2007. It is one of a handful of the world's major experiments working towards the observation of gravitational waves....
, GEO 600
GEO 600
GEO 600 is a gravitational wave detector located near Sarstedt, Germany. This instrument, and its sister interferometric detectors, when operational, are some of the most sensitive gravitational wave detectors ever designed...
, and TAMA 300
TAMA 300
TAMA 300 is a gravitational wave detector located at the Mitaka campus of the National Astronomical Observatory of Japan. It is a project of the gravitational wave studies group at the Institute for Cosmic Ray Research of the University of Tokyo...
should increase the sensitivity still further; the next generation of instruments (Advanced LIGO and Advanced Virgo) will be more than ten times more sensitive. Another highly sensitive interferometer (LCGT
LCGT
The Large Scale Cryogenic Gravitational Wave Telescope is a future project of the gravitational wave studies group at the Institute for Cosmic Ray Research of the University of Tokyo. The ICRR was established in 1976 for cosmic ray studies, and is currently working on TAMA 300...
) is currently in the design phase. A key point is that a tenfold increase in sensitivity (radius of 'reach') increases the volume of space accessible to the instrument by one thousand times. This increases the rate at which detectable signals should be seen from one per tens of years of observation, to tens per year.
Interferometric detectors are limited at high frequencies by shot noise
Shot noise
Shot noise is a type of electronic noise that may be dominant when the finite number of particles that carry energy is sufficiently small so that uncertainties due to the Poisson distribution, which describes the occurrence of independent random events, are of significance...
, which occurs because the lasers produce photons randomly; one analogy is to rainfall—the rate of rainfall, like the laser intensity, is measurable, but the raindrops, like photons, fall at random times, causing fluctuations around the average value. This leads to noise at the output of the detector, much like radio static. In addition, for sufficiently high laser power, the random momentum transferred to the test masses by the laser photons shakes the mirrors, masking signals at low frequencies. Thermal noise (e.g., Brownian motion
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
) is another limit to sensitivity. In addition to these 'stationary' (constant) noise sources, all ground-based detectors are also limited at low frequencies by seismic noise and other forms of environmental vibration, and other 'non-stationary' noise sources; creaks in mechanical structures, lightning or other large electrical disturbances, etc. may also create noise masking an event or may even imitate an event. All these must be taken into account and excluded by analysis before a detection may be considered a true gravitational wave event.
Space-based interferometers, such as LISA
Laser Interferometer Space Antenna
The Laser Interferometer Space Antenna is a planned space mission to detect and accurately measure gravitational waves from astronomical sources. LISA was originally conceived as a joint effort between the United States space agency NASA and the European Space Agency...
and DECIGO, are also being developed. LISA's design calls for three test masses forming an equilateral triangle, with lasers from each spacecraft to each other spacecraft forming two independent interferometers. LISA is planned to occupy a solar orbit trailing the Earth, with each arm of the triangle being five million kilometers. This puts the detector in an excellent vacuum
Interplanetary medium
The interplanetary medium is the material which fills the solar system and through which all the larger solar system bodies such as planets, asteroids and comets move.-Composition and physical characteristics:...
far from Earth-based sources of noise, though it will still be susceptible to shot noise, as well as artifacts caused by cosmic ray
Cosmic ray
Cosmic rays are energetic charged subatomic particles, originating from outer space. They may produce secondary particles that penetrate the Earth's atmosphere and surface. The term ray is historical as cosmic rays were thought to be electromagnetic radiation...
s and solar wind
Solar wind
The solar wind is a stream of charged particles ejected from the upper atmosphere of the Sun. It mostly consists of electrons and protons with energies usually between 1.5 and 10 keV. The stream of particles varies in temperature and speed over time...
.
There are currently two detectors focusing on detection at the higher end of the gravitational wave spectrum (10−7 to 105 Hz): one at University of Birmingham
University of Birmingham
The University of Birmingham is a British Redbrick university located in the city of Birmingham, England. It received its royal charter in 1900 as a successor to Birmingham Medical School and Mason Science College . Birmingham was the first Redbrick university to gain a charter and thus...
, England, and the other at INFN
Istituto Nazionale di Fisica Nucleare
The Istituto Nazionale di Fisica Nucleare is the coordinating institution for nuclear, particle and astroparticle physics in Italy. It was founded on the 8th of August 1951, to further the nuclear physics research tradition initiated by Enrico Fermi in Rome, in the 1930s...
Genoa, Italy. A third is under development at Chongqing University
Chongqing University
Chongqing University is a comprehensive national university in the Shapingba District of Chongqing municipality, China. It is a member of the Project 211 and Project 985 which aims to transform Chinese universities into better research institutions.-History:...
, China. The Birmingham detector measures changes in the polarization state of a microwave
Microwave
Microwaves, a subset of radio waves, have wavelengths ranging from as long as one meter to as short as one millimeter, or equivalently, with frequencies between 300 MHz and 300 GHz. This broad definition includes both UHF and EHF , and various sources use different boundaries...
beam circulating in a closed loop about one meter across. Two have been fabricated and they are currently expected to be sensitive to periodic spacetime strains of
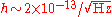 , given as an amplitude spectral density
, given as an amplitude spectral densitySpectral density
In statistical signal processing and physics, the spectral density, power spectral density , or energy spectral density , is a positive real function of a frequency variable associated with a stationary stochastic process, or a deterministic function of time, which has dimensions of power per hertz...
. The INFN Genoa detector is a resonant antenna consisting of two coupled spherical superconducting harmonic oscillators a few centimeters in diameter. The oscillators are designed to have (when uncoupled) almost equal resonant frequencies. The system is currently expected to have a sensitivity to periodic spacetime strains of
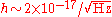 , with an expectation to reach a sensitivity of
, with an expectation to reach a sensitivity of  . The Chongqing University detector is planned to detect relic high-frequency gravitational waves with the predicted typical parameters ?g ~ 1010 Hz (10 GHz) and h ~ 10−30-10−31.
. The Chongqing University detector is planned to detect relic high-frequency gravitational waves with the predicted typical parameters ?g ~ 1010 Hz (10 GHz) and h ~ 10−30-10−31.Einstein@Home
In some sense, the easiest signals to detect should be constant sources. Supernovae and neutron star or black hole mergers should have larger amplitudes and be more interesting, but the waves generated will be more complicated. The waves given off by a spinning, aspherical neutron star would be "monochromaticMonochrome
Monochrome describes paintings, drawings, design, or photographs in one color or shades of one color. A monochromatic object or image has colors in shades of limited colors or hues. Images using only shades of grey are called grayscale or black-and-white...
"—like a pure tone
Pure tone
A pure tone is a tone with a sinusoidal waveshape.A sine wave is characterized by its frequency, the number of cycles per second—or its wavelength, the distance the waveform travels through its medium within a period—and the amplitude, the size of each cycle...
in acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
. It would not change very much in amplitude or frequency.
The Einstein@Home
Einstein@Home
Einstein@Home is a volunteer distributed computing project hosted by the University of Wisconsin–Milwaukee and the Max Planck Institute for Gravitational Physics . The project is directed by Bruce Allen...
project is a distributed computing
Distributed computing
Distributed computing is a field of computer science that studies distributed systems. A distributed system consists of multiple autonomous computers that communicate through a computer network. The computers interact with each other in order to achieve a common goal...
project similar to SETI@home
SETI@home
SETI@home is an Internet-based public volunteer computing project employing the BOINC software platform, hosted by the Space Sciences Laboratory, at the University of California, Berkeley, in the United States. SETI is an acronym for the Search for Extra-Terrestrial Intelligence...
intended to detect this type of simple gravitational wave. By taking data from LIGO and GEO, and sending it out in little pieces to thousands of volunteers for parallel analysis on their home computers, Einstein@Home can sift through the data far more quickly than would be possible otherwise.
Mathematics
Einstein's equations form the fundamental law of general relativity. The curvature of spacetime can be expressed mathematically using the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
— denoted
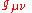 . The metric holds information regarding how distances are measured in the space under consideration. Because the propagation of gravitational waves through space and time change distances, we will need to use this to find the solution to the wave equation.
. The metric holds information regarding how distances are measured in the space under consideration. Because the propagation of gravitational waves through space and time change distances, we will need to use this to find the solution to the wave equation.Spacetime curvature is also expressed with respect to a covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
,
 , in the form of the Einstein tensor
, in the form of the Einstein tensorEinstein tensor
In differential geometry, the Einstein tensor , named after Albert Einstein, is used to express the curvature of a Riemannian manifold...
—
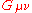 . This curvature is related to the stress-energy tensor
. This curvature is related to the stress-energy tensorStress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
—
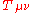 — by the key equation
— by the key equation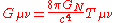 ,
,where
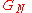 is Newton's gravitational constant
is Newton's gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
, and
 is the speed of light. We assume geometrized units, so
is the speed of light. We assume geometrized units, so  .
.With some simple assumptions, Einstein's equations can be rewritten to show explicitly that they are wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
s. To begin with, we adopt some coordinate system, like
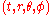 . We define the "flat-space metric"
. We define the "flat-space metric" 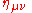 to be the quantity which — in this coordinate system — has the components we would expect for the flat space metric. For example, in these spherical coordinates, we have
to be the quantity which — in this coordinate system — has the components we would expect for the flat space metric. For example, in these spherical coordinates, we have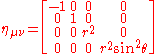 .
.This flat-space metric has no physical significance; it is a purely mathematical device necessary for the analysis. Tensor indices are raised and lowered using this "flat-space metric".
Now, we can also think of the physical metric
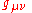 as a matrix
as a matrixMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
, and find its determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
,
 . Finally, we define a quantity
. Finally, we define a quantity .
.This is the crucial field, which will represent the radiation. It is possible (at least in an asymptotically flat spacetime
Asymptotically flat spacetime
An asymptotically flat spacetime is a Lorentzian manifold in which, roughly speaking, the curvature vanishes at large distances from some region, so that at large distances, the geometry becomes indistinguishable from that of Minkowski spacetime....
) to choose the coordinates in such a way that this quantity satisfies the "de Donder" gauge conditions (conditions on the coordinates):
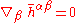 ,
,where
 represents the flat-space derivative operator. These equations say that the divergence
represents the flat-space derivative operator. These equations say that the divergenceDivergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the field is zero. The full, nonlinear Einstein equations can now be written as
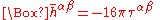 ,
,where
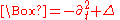 represents the flat-space d'Alembertian operator, and
represents the flat-space d'Alembertian operator, and 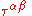 represents the stress-energy tensor plus quadratic terms involving
represents the stress-energy tensor plus quadratic terms involving 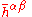 . This is just a wave equation for the field with a source, despite the fact that the source involves terms quadratic in the field itself. That is, it can be shown that solutions to this equation are waves traveling with velocity 1 in these coordinates.
. This is just a wave equation for the field with a source, despite the fact that the source involves terms quadratic in the field itself. That is, it can be shown that solutions to this equation are waves traveling with velocity 1 in these coordinates.Linear approximation
The equations above are valid everywhere — near a black hole, for instance. However, because of the complicated source term, the solution is generally too difficult to find analytically. We can often assume that space is nearly flat, so the metric is nearly equal to the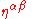 tensor. In this case, we can neglect terms quadratic in
tensor. In this case, we can neglect terms quadratic in 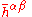 , which means that the
, which means that the 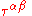 field reduces to the usual stress-energy tensor
field reduces to the usual stress-energy tensor 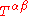 . That is, Einstein's equations become
. That is, Einstein's equations become .
.If we are interested in the field far from a source, however, we can treat the source as a point source; everywhere else, the stress-energy tensor would be zero, so
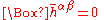 .
.Now, this is the usual homogeneous wave equation — one for each component of
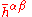 . Solutions to this equation are well known. For a wave moving away from a point source, the radiated part (meaning the part that dies off as
. Solutions to this equation are well known. For a wave moving away from a point source, the radiated part (meaning the part that dies off as 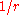 far from the source) can always be written in the form
far from the source) can always be written in the form 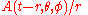 , where
, where 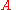 is just some function. It can be shown that — to a linear approximation — it is always possible to make the field traceless. Now, if we further assume that the source is positioned at
is just some function. It can be shown that — to a linear approximation — it is always possible to make the field traceless. Now, if we further assume that the source is positioned at  , the general solution to the wave equation in spherical coordinates is
, the general solution to the wave equation in spherical coordinates is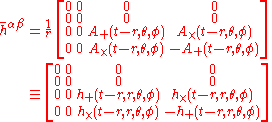
where we now see the origin of the two polarizations.
Relation to the source
If we know the details of a source — for instance, the parameters of the orbit of a binary — we can relate the source's motion to the gravitational radiation observed far away. With the relation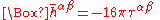 ,
,we can write the solution in terms of the tensorial Green's function
Green's function
In mathematics, a Green's function is a type of function used to solve inhomogeneous differential equations subject to specific initial conditions or boundary conditions...
for the d'Alembertian operator:
 .
.Though it is possible to expand the Green's function in tensor spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
, it is easier to simply use the form
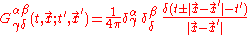 ,
,where the positive and negative signs correspond to ingoing and outgoing solutions, respectively. Generally, we are interested in the outgoing solutions, so
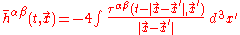 .
.If the source is confined to a small region very far away, to an excellent approximation we have:
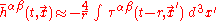 ,
,where
 .
.Now, because we will eventually only be interested in the spatial components of this equation (time components can be set to zero with a coordinate transformation), and we are integrating this quantity — presumably over a region of which there is no boundary — we can put this in a different form. Ignoring divergences with the help of Stokes' theorem
Stokes' theorem
In differential geometry, Stokes' theorem is a statement about the integration of differential forms on manifolds, which both simplifies and generalizes several theorems from vector calculus. Lord Kelvin first discovered the result and communicated it to George Stokes in July 1850...
and an empty boundary, we can see that
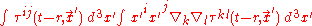 ,
,Inserting this into the above equation, we arrive at
 ,
,Finally, because we have chosen to work in coordinates for which
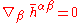 , we know that
, we know that 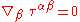 . With a few simple manipulations, we can use this to prove that
. With a few simple manipulations, we can use this to prove that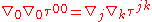 .
.With this relation, the expression for the radiated field is
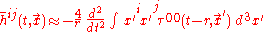 .
.In the linear case,
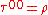 , the density of mass-energy.
, the density of mass-energy.To a very good approximation, the density of a simple binary can be described by a pair of delta-functions, which eliminates the integral. Explicitly, if the masses of the two objects are
 and
and  , and the positions are
, and the positions are 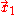 and
and 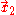 , then
, then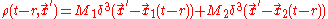 .
.We can use this expression to do the integral above:
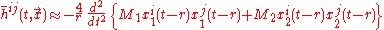 .
.Using mass-centered coordinates, and assuming a circular binary, this is
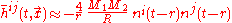 ,
,where
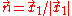 . Plugging in the known values of
. Plugging in the known values of 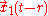 , we obtain the expressions given above for the radiation from a simple binary.
, we obtain the expressions given above for the radiation from a simple binary.Criticism
Not all theories agree upon the existence of the relativistic gravitational wavesdefined as: (1) the small fluctuations of curved spacetime which (2) have been separated from its source and propagate independently.
For instance, theory of superfluid vacuum
Superfluid vacuum
Superfluid vacuum theory , sometimes dubbed as the theory of BEC vacuum, is an approach in theoretical physics and quantum mechanics where the physical vacuum is viewed as a superfluid or BEC....
brings into question that the relativistic object possessing both of these properties may exist in Nature.
Indeed, according to the approach, the curved spacetime itself is the small collective excitation of the superfluid background, therefore,
the property (1) means that the gravitational wave would be in fact the "small fluctuation of the small fluctuation" which does not look like the physical concept
(as if somebody tried to introduce small fluctuations inside phonons, for instance).
As a result, it may be not just a coincidence that in general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
the gravitational field alone has no well-defined stress-energy tensor
Stress-energy tensor
The stress–energy tensor is a tensor quantity in physics that describes the density and flux of energy and momentum in spacetime, generalizing the stress tensor of Newtonian physics. It is an attribute of matter, radiation, and non-gravitational force fields...
,
only the pseudotensor
Stress-energy-momentum pseudotensor
In the theory of general relativity, a stress–energy–momentum pseudotensor, such as the Landau–Lifshitz pseudotensor, is an extension of the non-gravitational stress–energy tensor which incorporates the energy-momentum of gravity. It allows the energy-momentum of a system of gravitating matter to...
one.
Therefore, the property (2) cannot be completely justified in a theory with exact Lorentz symmetry which the general relativity is.
Though, SVT does not a priori forbid an existence of the non-localized wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
-like excitations of the superfluid background
which might be responsible for the astrophysical phenomena
which are currently being attributed to gravitational waves, such as the Hulse-Taylor binary. However, such excitations cannot be correctly described within the framework of a relativistic
Theory of relativity
The theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
theory.
See also
- Spin-flipSpin-flipA black hole spin-flip occurs when the spin axis of a rotating black hole undergoes a sudden change in orientation due to absorption of a second black hole....
, a consequence of gravitational wave emission from binary supermassive black holeSupermassive black holeA supermassive black hole is the largest type of black hole in a galaxy, in the order of hundreds of thousands to billions of solar masses. Most, and possibly all galaxies, including the Milky Way, are believed to contain supermassive black holes at their centers.Supermassive black holes have...
s - Gravitational fieldGravitational fieldThe gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
- Orbital resonanceOrbital resonanceIn celestial mechanics, an orbital resonance occurs when two orbiting bodies exert a regular, periodic gravitational influence on each other, usually due to their orbital periods being related by a ratio of two small integers. Orbital resonances greatly enhance the mutual gravitational influence of...
- Tidal forceTidal forceThe tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
External links
- The LISA Brownbag – Selection of the most significant e-prints related to LISA science
- Astroparticle.org. To know everything about astroparticle physics, including gravitational waves
- Caltech's Physics 237-2002 Gravitational Waves by Kip Thorne Video plus notes: Graduate level but does not assume knowledge of General Relativity, Tensor Analysis, or Differential Geometry; Part 1: Theory (10 lectures), Part 2: Detection (9 lectures)
- www.astronomycast.com January 14, 2008 Episode 71: Gravitational Waves
- Laser Interferometer Gravitational Wave Observatory. LIGO Laboratory, operated by the California Institute of TechnologyCalifornia Institute of TechnologyThe California Institute of Technology is a private research university located in Pasadena, California, United States. Caltech has six academic divisions with strong emphases on science and engineering...
and the Massachusetts Institute of TechnologyMassachusetts Institute of TechnologyThe Massachusetts Institute of Technology is a private research university located in Cambridge, Massachusetts. MIT has five schools and one college, containing a total of 32 academic departments, with a strong emphasis on scientific and technological education and research.Founded in 1861 in... - The LIGO Scientific Collaboration
- Einstein's Messengers – The LIGO Movie by NSFNational Science FoundationThe National Science Foundation is a United States government agency that supports fundamental research and education in all the non-medical fields of science and engineering. Its medical counterpart is the National Institutes of Health...
- Home page for Einstein@Home project, a distributed computing project processing raw data from LIGO Laboratory, searching for gravity waves
- The National Center for Supercomputing Applications – a numerical relativity group
- Caltech Relativity Tutorial – A basic introduction to gravitational waves, and astrophysical systems giving off gravitational waves
- Resource Letter GrW-1: Gravitational waves – a list of books, journals and web resources compiled by Joan Centrella for research into gravitational waves
- Mathematical and Physical Perspectives on Gravitational Radiation – written by B F Schutz of the Max Planck Institute explaining the significance and background of some key concepts in gravitational radiation
- Binary BH Merger – estimating the radiated power and merger time of a BH binary using dimensional analysis

