
Multipole expansion
Encyclopedia
A multipole expansion is a mathematical series
representing a function
that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original function. The function being expanded may be complex
in general. Multipole expansions are very frequently used in the study of electromagnetic
and gravitational field
s, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space.
The multipole expansion is expressed as a sum of terms with progressively finer angular features. For example, the initial term — called the zero-th, or monopole, moment
— is a constant, independent of angle. The following term — the first, or dipole
, moment — varies once from positive to negative around the sphere. Higher-order terms (like the quadrupole
and octupole) vary more quickly with angles.
. Thus, we might write a function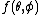 as the sum
as the sum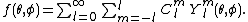
Here,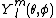 are the standard spherical harmonics, and
are the standard spherical harmonics, and 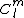 are constant coefficients which depend on the function. The term
are constant coefficients which depend on the function. The term 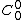 represents the monopole;
represents the monopole; 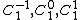 represent the dipole; and so on. Equivalently, the series is also frequently written as
represent the dipole; and so on. Equivalently, the series is also frequently written as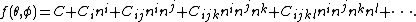
Here, each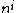 represents a unit vector in the direction given by the angles
represents a unit vector in the direction given by the angles 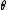 and
and 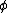 , and indices are implicitly summed. Here, the term
, and indices are implicitly summed. Here, the term 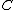 is the monopole;
is the monopole;  is a set of three numbers representing the dipole; and so on.
is a set of three numbers representing the dipole; and so on.
In the above expansions, the coefficients may be real or complex. If the function being expressed as a multipole expansion is real, however, the coefficients must satisfy certain properties. In the spherical harmonic expansion, we must have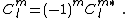
In the multi-vector expansion, each coefficient must be real:
While expansions of scalar
functions are by far the most common application of multipole expansions, they may also be generalized to describe tensor
s of arbitrary rank. This finds use in multipole expansions of the vector potential
in electromagnetism, or the metric perturbation in the description of gravitational wave
s.
For describing functions of three dimensions, away from the coordinate origin, the coefficients of the multipole expansion can be written as functions of the distance to the origin, -- most frequently, as a Laurent series
-- most frequently, as a Laurent series
in powers of . For example, to describe the electromagnetic potential,
. For example, to describe the electromagnetic potential,  , from a source in a small region near the origin, the coefficients may be written as:
, from a source in a small region near the origin, the coefficients may be written as:
s of systems of mass
es, electric and magnetic field
s of charge and current distributions, and the propagation of electromagnetic waves. A classic example is the calculation of the exterior
multipole moments of atomic nuclei from their interaction
energies with the interior multipoles of the electronic orbitals.
The multipole moments of the nuclei report on the distribution of charges
within the nucleus and, thus, on the shape of the nucleus. Truncation of
the multipole expansion to its first non-zero term is often useful for
theoretical calculations.
Multipole expansions are also useful in numerical simulations, and form
the basis of the Fast Multipole Method
of Greengard
and Rokhlin
, a general technique for efficient computation of energies
and forces in systems of interacting particles. The basic idea is to decompose the particles into groups; particles within a group interact
normally (i.e., by the full potential), whereas the energies and forces
between groups of particles are calculated from their multipole moments.
The efficiency of the fast multipole method is generally similar to that
of Ewald summation
, but is superior if the particles are clustered,
i.e., if the system has large density fluctuations.
in the Cartesian coordinates x, y and z, while the second is in terms of spherical harmonics
which depend on spherical polar coordinates. The Cartesian approach has the advantage that no prior knowledge of Legendre functions, spherical harmonics, etc., is required. Its disadvantage is that the derivations are fairly cumbersome (in fact a large part of it is the implicit rederivation of the Legendre expansion of 1/|r-R|, which was done once and for all by Legendre
in the 1780s).
Also it is difficult to give a closed expression for a general term of the multipole expansion—usually only the first few terms are given followed by some dots.
of an arbitrary function v(r-R) around the origin r = 0 is,
with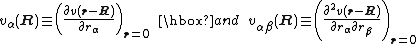
If v(r-R) satisfies the Laplace equation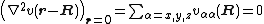
then the expansion can be rewritten in terms of the components of a traceless Cartesian second rank tensor
,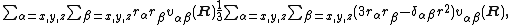
where δαβ is the Kronecker delta and r2 ≡ |r|2.
Removing the trace is common, because it takes the rotational invariant r2 out of the second rank tensor.
Example
Consider now the following form of v(r-R),
then by direct differentiation it follows that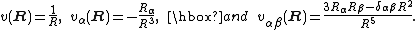
Define a monopole, dipole and (traceless) quadrupole by, respectively,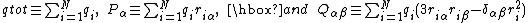
and we obtain finally the first few terms of the multipole expansion of the total potential, which is the sum of the Coulomb potentials of the separate charges,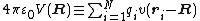
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
representing a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original function. The function being expanded may be complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
in general. Multipole expansions are very frequently used in the study of electromagnetic
Electromagnetic field
An electromagnetic field is a physical field produced by moving electrically charged objects. It affects the behavior of charged objects in the vicinity of the field. The electromagnetic field extends indefinitely throughout space and describes the electromagnetic interaction...
and gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
s, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space.
The multipole expansion is expressed as a sum of terms with progressively finer angular features. For example, the initial term — called the zero-th, or monopole, moment
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
— is a constant, independent of angle. The following term — the first, or dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
, moment — varies once from positive to negative around the sphere. Higher-order terms (like the quadrupole
Quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
and octupole) vary more quickly with angles.
Expansion in spherical harmonics
Most commonly, the series is written as a sum of spherical harmonicsSpherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
. Thus, we might write a function
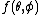 as the sum
as the sum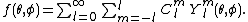
Here,
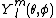 are the standard spherical harmonics, and
are the standard spherical harmonics, and 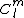 are constant coefficients which depend on the function. The term
are constant coefficients which depend on the function. The term 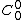 represents the monopole;
represents the monopole; 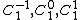 represent the dipole; and so on. Equivalently, the series is also frequently written as
represent the dipole; and so on. Equivalently, the series is also frequently written as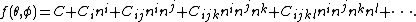
Here, each
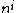 represents a unit vector in the direction given by the angles
represents a unit vector in the direction given by the angles 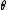 and
and 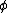 , and indices are implicitly summed. Here, the term
, and indices are implicitly summed. Here, the term 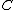 is the monopole;
is the monopole;  is a set of three numbers representing the dipole; and so on.
is a set of three numbers representing the dipole; and so on.In the above expansions, the coefficients may be real or complex. If the function being expressed as a multipole expansion is real, however, the coefficients must satisfy certain properties. In the spherical harmonic expansion, we must have
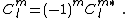
In the multi-vector expansion, each coefficient must be real:

While expansions of scalar
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
functions are by far the most common application of multipole expansions, they may also be generalized to describe tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
s of arbitrary rank. This finds use in multipole expansions of the vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
in electromagnetism, or the metric perturbation in the description of gravitational wave
Gravitational wave
In physics, gravitational waves are theoretical ripples in the curvature of spacetime which propagates as a wave, traveling outward from the source. Predicted to exist by Albert Einstein in 1916 on the basis of his theory of general relativity, gravitational waves theoretically transport energy as...
s.
For describing functions of three dimensions, away from the coordinate origin, the coefficients of the multipole expansion can be written as functions of the distance to the origin,
 -- most frequently, as a Laurent series
-- most frequently, as a Laurent seriesLaurent series
In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where...
in powers of
 . For example, to describe the electromagnetic potential,
. For example, to describe the electromagnetic potential,  , from a source in a small region near the origin, the coefficients may be written as:
, from a source in a small region near the origin, the coefficients may be written as:
Applications of multipole expansions
Multipole expansions are widely used in problems involving gravitational fieldGravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
s of systems of mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
es, electric and magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s of charge and current distributions, and the propagation of electromagnetic waves. A classic example is the calculation of the exterior
multipole moments of atomic nuclei from their interaction
energies with the interior multipoles of the electronic orbitals.
The multipole moments of the nuclei report on the distribution of charges
within the nucleus and, thus, on the shape of the nucleus. Truncation of
the multipole expansion to its first non-zero term is often useful for
theoretical calculations.
Multipole expansions are also useful in numerical simulations, and form
the basis of the Fast Multipole Method
Fast Multipole Method
The fast multipole method is a mathematical technique that was developed to speed up the calculation of long-ranged forces in the n-body problem...
of Greengard
Leslie Greengard
Leslie F. Greengard is an American mathematician, doctor of medicine and computer scientist. He is co-inventor of the fast multipole method in 1987, recognised as one of the top-ten algorithms of the 20th century....
and Rokhlin
Vladimir Rokhlin (American scientist)
Vladimir Rokhlin is mathematician and professor of computer science and mathematics at the Yale University. He is co-inventor of the fast multipole method in 1987, recognised as one of the top-ten algorithms of the 20th century.-Short biography:Vladimir Rokhlin was born on August 4, 1952 in...
, a general technique for efficient computation of energies
and forces in systems of interacting particles. The basic idea is to decompose the particles into groups; particles within a group interact
normally (i.e., by the full potential), whereas the energies and forces
between groups of particles are calculated from their multipole moments.
The efficiency of the fast multipole method is generally similar to that
of Ewald summation
Ewald summation
Ewald summation, named after Paul Peter Ewald, is a method for computing the interaction energies of periodic systems , particularly electrostatic energies. Ewald summation is a special case of the Poisson summation formula, replacing the summation of interaction energies in real space with an...
, but is superior if the particles are clustered,
i.e., if the system has large density fluctuations.
Multipole expansion of a potential outside an electrostatic charge distribution
Consider a discrete charge distribution consisting of N point charges qi with position vectors ri. We assume the charges to be clustered around the origin, so that for all i: ri < rmax, where rmax has some finite value. The potential V(R), due to the charge distribution, at a point R outside the charge distribution, i.e., |R| > rmax, can be expanded in powers of 1/R. Two ways of making this expansion can be found in the literature. The first is a Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
in the Cartesian coordinates x, y and z, while the second is in terms of spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
which depend on spherical polar coordinates. The Cartesian approach has the advantage that no prior knowledge of Legendre functions, spherical harmonics, etc., is required. Its disadvantage is that the derivations are fairly cumbersome (in fact a large part of it is the implicit rederivation of the Legendre expansion of 1/|r-R|, which was done once and for all by Legendre
Adrien-Marie Legendre
Adrien-Marie Legendre was a French mathematician.The Moon crater Legendre is named after him.- Life :...
in the 1780s).
Also it is difficult to give a closed expression for a general term of the multipole expansion—usually only the first few terms are given followed by some dots.
Expansion in Cartesian coordinates
The Taylor expansionTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of an arbitrary function v(r-R) around the origin r = 0 is,

with
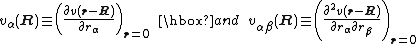
If v(r-R) satisfies the Laplace equation
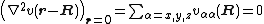
then the expansion can be rewritten in terms of the components of a traceless Cartesian second rank tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
,
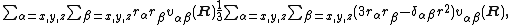
where δαβ is the Kronecker delta and r2 ≡ |r|2.
Removing the trace is common, because it takes the rotational invariant r2 out of the second rank tensor.
Example
Consider now the following form of v(r-R),

then by direct differentiation it follows that
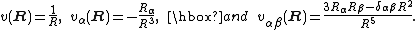
Define a monopole, dipole and (traceless) quadrupole by, respectively,
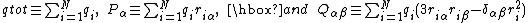
and we obtain finally the first few terms of the multipole expansion of the total potential, which is the sum of the Coulomb potentials of the separate charges,
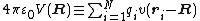
-
-
-
-

This expansion of the potential of a discrete charge distribution is very similar to the one in real solid harmonics given below. The main difference is that the present one is in terms of linear dependent quantities, for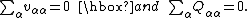
Note
If the charge distribution consists of two charges of opposite sign which are an infinitesimal distance d apart, so that d/R >> (d/R)2, it is easily shown that the
only non-vanishing term in the expansion is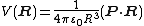 ,
,
the electric dipolar potential field.
Spherical form
The potential V(R) at a point R outside the charge distribution, i.e., |R| > rmax, can be expanded by the Laplace expansionLaplace expansion (potential)In physics, the Laplace expansion of a 1/r - type potential is applied to expand Newton's gravitational potential or Coulomb's electrostatic potential. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the interelectronic repulsion.The Laplace...
,

where is an irregular solid harmonic (defined below as a spherical harmonicSpherical HarmonicSpherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
is an irregular solid harmonic (defined below as a spherical harmonicSpherical HarmonicSpherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
function divided by Rl+1) and is a regular solid harmonic (a spherical harmonic times rl). We define the spherical multipole moment of the charge distribution as follows
is a regular solid harmonic (a spherical harmonic times rl). We define the spherical multipole moment of the charge distribution as follows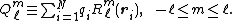
Note that a multipole moment is solely determined by the charge distribution (the positions and magnitudes of the N charges).
A spherical harmonicSpherical HarmonicSpherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
depends on the unit vector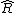 . (A unit vector is determined by two spherical polar angles.) Thus, by definition, the irregular solid harmonics can be written as
. (A unit vector is determined by two spherical polar angles.) Thus, by definition, the irregular solid harmonics can be written as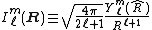
so that the multipole expansion of the field V(R) at the point R outside the charge distribution is given by
-
-

This expansion is completely general in that it gives a closed form for all terms, not just for the first few. It shows that the spherical multipole momentsSpherical multipole momentsSpherical multipole moments are the coefficients in a series expansionof a potential that varies inversely with the distance R to a source, i.e., as 1/R...
appear as coefficients in the 1/R expansion of the potential.
It is of interest to consider the first few terms in real form, which are the only terms commonly found in undergraduate textbooks.
Since the summand of the m summation is invariant under a unitary transformation
of both factors simultaneously and since transformation of complex spherical harmonics to real form is by a unitary transformation, we can simply substitute real irregular solid harmonics and real multipole moments. The l = 0 term becomes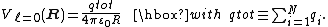
This is in fact Coulomb's lawCoulomb's lawCoulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
again.
For the l = 1 term we introduce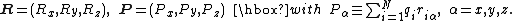
Then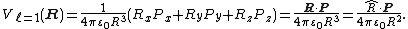
This term is identical to the one found in Cartesian form.
In order to write the l=2 term, we have to introduce short-hand notations for the five real components of the quadrupole moment and the real spherical harmonics. Notations of the type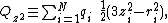
can be found in the literature. Clearly the real notation becomes awkward very soon, exhibiting the usefulness of the complex notation.
Interaction of two non-overlapping charge distributions
Consider two sets of point charges, one set {qi } clustered around a point A and one set {qj } clustered around a point B. Think for example of two moleculeMoleculeA molecule is an electrically neutral group of at least two atoms held together by covalent chemical bonds. Molecules are distinguished from ions by their electrical charge...
s, and recall that a molecule by definition consists of electrons (negative point charges) and nuclei (positive point charges).
The total electrostatic interaction energy UAB between the two distributions is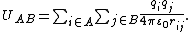
This energy can be expanded in a power series in the inverse distance of A and B.
This expansion is known as the multipole expansion of UAB.
In order to derive this multipole expansion, we write rXY = rY-rX, which is a vector pointing from X towards Y. Note that
We assume that the two distributions do not overlap: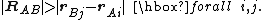
Under this condition we may apply the Laplace expansionLaplace expansion (potential)In physics, the Laplace expansion of a 1/r - type potential is applied to expand Newton's gravitational potential or Coulomb's electrostatic potential. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the interelectronic repulsion.The Laplace...
in the following form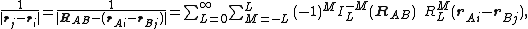
where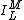 and
and 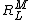 are irregular and regular solid harmonics, respectively.
are irregular and regular solid harmonics, respectively.
The translation of the regular solid harmonic gives a finite expansion,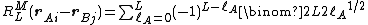
-
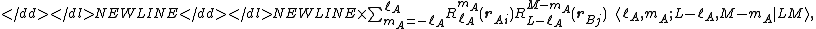
where the quantity between pointed brackets is a Clebsch-Gordan coefficient. Further we used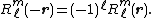
Use of the definition of spherical multipoles Qml and covering of the summation ranges in a somewhat different order (which is only allowed for an infinite range of L) gives finally
-
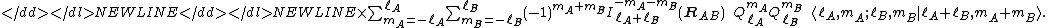
This is the multipole expansion of the interaction energy of two non-overlapping charge distributions which are a distance RAB apart. Since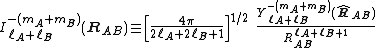
this expansion is manifestly in powers of 1/RAB. The function Yml is a normalized spherical harmonicSpherical HarmonicSpherical Harmonic is a science fiction novel from the Saga of the Skolian Empire by Catherine Asaro. It tells the story of Dyhianna Selei , the Ruby Pharaoh of the Skolian Imperialate, as she strives to reform her government and reunite her family in the aftermath of a devastating interstellar...
.
Examples of multipole expansions
There are many types of multipole moments, since there are many types of potentialPotential*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
s
and many ways of approximating a potential by a series expansionSeries expansionIn mathematics, a series expansion is a method for calculating a function that cannot be expressed by just elementary operators . The resulting so-called series often can be limited to a finite number of terms, thus yielding an approximation of the function...
, depending on the
coordinates and the symmetrySymmetrySymmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
of the charge distribution. The most common expansions
include:
- Axial multipole momentsAxial multipole momentsAxial multipole moments are a series expansionof the electric potential of acharge distribution localized close tothe origin along oneCartesian axis,denoted here as the z-axis...
of a potential;
potential; - Spherical multipole momentsSpherical multipole momentsSpherical multipole moments are the coefficients in a series expansionof a potential that varies inversely with the distance R to a source, i.e., as 1/R...
of a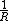 potential; and
potential; and - Cylindrical multipole momentsCylindrical multipole momentsCylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as \ln \ R...
of a potential
potential
Examples of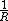 potentials include the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
potentials include the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
,
the magnetic potentialMagnetic potentialThe term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
and the gravitational potential of point sources. An example
of a potential is the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
potential is the electric potentialElectric potentialIn classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
of an infinite line charge.
General mathematical properties
Mathematically, multipole expansions are related to the underlying rotational symmetry of the physical laws and their associated differential equations. Even though the source terms (such as the masses, charges, or currents) may not be symmetrical, one can expand them in terms of irreducible representationsGroup representationIn the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
of the rotational symmetry groupSymmetry groupThe symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
, which leads to spherical harmonics and related sets of orthogonal functions. One uses the technique of separation of variablesSeparation of variablesIn mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
to extract the corresponding solutions for the radial dependencies.
See also
- Multipole momentsMultipole momentsIn mathematics, especially as applied to physics, multipole moments are the coefficients of a series expansion of a potential due to continuous or discrete sources . A multipole moment usually involves powers of the distance to the origin, as well as some angular dependence...
- Axial multipole momentsAxial multipole momentsAxial multipole moments are a series expansionof the electric potential of acharge distribution localized close tothe origin along oneCartesian axis,denoted here as the z-axis...
- Spherical multipole momentsSpherical multipole momentsSpherical multipole moments are the coefficients in a series expansionof a potential that varies inversely with the distance R to a source, i.e., as 1/R...
- Cylindrical multipole momentsCylindrical multipole momentsCylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as \ln \ R...
- Quadrupole magnetQuadrupole magnetQuadrupole magnets consist of groups of four magnets laid out so that in the multipole expansion of the field the dipole terms cancel and where the lowest significant terms in the field equations are quadrupole. Quadrupole magnets are useful as they create a magnetic field whose magnitude grows...
s are used in particle acceleratorParticle acceleratorA particle accelerator is a device that uses electromagnetic fields to propel charged particles to high speeds and to contain them in well-defined beams. An ordinary CRT television set is a simple form of accelerator. There are two basic types: electrostatic and oscillating field accelerators.In...
s - MonopoleMonopoleMonopole may refer to:*Magnetic monopole, or Dirac monopole, a hypothetical particle that may be loosely described as a magnet with only one pole, or related concepts in physics and mathematics:...
- DipoleDipoleIn physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
- QuadrupoleQuadrupoleA quadrupole or quadrapole is one of a sequence of configurations of—for example—electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity.-Mathematical...
- Solid harmonics
- Laplace expansionLaplace expansion (potential)In physics, the Laplace expansion of a 1/r - type potential is applied to expand Newton's gravitational potential or Coulomb's electrostatic potential. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the interelectronic repulsion.The Laplace...
- Legendre polynomials
- Axial multipole moments
-
-
-
-
-
-
-

