For other meanings of the term "orbit", see orbit (disambiguation)

Orbit (disambiguation)

Orbit is the gravitationally curved path of one object around a point or another body.Orbit may also refer to:-Computing:* ORBit, an object request broker for CORBA* Orbit Downloader, a download manager for Windows-Science and mathematics:...

A circular orbit is the orbit

Orbit

In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...

 at a fixed distance around any point by an object rotating around a fixed axis

Rotation around a fixed axis

Rotation around a fixed axis is a special case of rotational motion. The fixed axis hypothesis exclude the possibility of a moving axis, and cannot describe such phenomena as wobbling or precession. According to Euler's rotation theorem, simultaneous rotation around more than one axis at the same...

.

Below we consider a circular orbit in astrodynamics

Astrodynamics

Orbital mechanics or astrodynamics is the application of ballistics and celestial mechanics to the practical problems concerning the motion of rockets and other spacecraft. The motion of these objects is usually calculated from Newton's laws of motion and Newton's law of universal gravitation. It...

 or celestial mechanics

Celestial mechanics

Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...

 under standard assumptions. Here the centripetal force

Centripetal force

Centripetal force is a force that makes a body follow a curved path: it is always directed orthogonal to the velocity of the body, toward the instantaneous center of curvature of the path. The mathematical description was derived in 1659 by Dutch physicist Christiaan Huygens...

 is the gravitational force, and the axis mentioned above is the line through the center of the central mass perpendicular to the plane of motion.

In this case not only the distance, but also the speed, angular speed, potential and kinetic energy are constant. There is no periapsis or apoapsis. This orbit has no radial version.

Circular acceleration

Transverse

Transversality

In mathematics, transversality is a notion that describes how spaces can intersect; transversality can be seen as the "opposite" of tangency, and plays a role in general position. It formalizes the idea of a generic intersection in differential topology...

 acceleration (perpendicular

Perpendicular

In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...

 to velocity) causes change in direction. If it is constant in magnitude and changing in direction with the velocity, we get a circular motion

Circular motion

In physics, circular motion is rotation along a circular path or a circular orbit. It can be uniform, that is, with constant angular rate of rotation , or non-uniform, that is, with a changing rate of rotation. The rotation around a fixed axis of a three-dimensional body involves circular motion of...

. For this centripetal acceleration we have


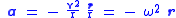
where:

• is orbital velocity
  Orbital velocity
  Orbital velocity can refer to the following:* The orbital speed of a body in a gravitational field.* The velocity of particles due to wave motion, in particular in wind waves....
  
   of orbiting body,
• is radius
  Radius
  In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
  
   of the circle
• is angular speed, measured in radians per second.

Velocity

The relative velocity is constant: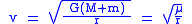
where:

• G is the gravitational constant
  Gravitational constant
  The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
  
  
• M and m are the masses of the orbiting bodies.
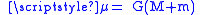• is the standard gravitational parameter
  Standard gravitational parameter
  In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
  
  .

Equation of motion

The orbit equation

Orbit equation

In astrodynamics an orbit equation defines the path of orbiting body m_2\,\! around central body m_1\,\! relative to m_1\,\!, without specifying position as a function of time...

 in polar coordinates, which in general gives r in terms of θ, reduces to:
where:

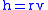• is specific angular momentum of the orbiting body.

This is just another way of writing again.

Angular speed and orbital period

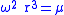
Hence the orbital period

Orbital period

The orbital period is the time taken for a given object to make one complete orbit about another object.When mentioned without further qualification in astronomy this refers to the sidereal period of an astronomical object, which is calculated with respect to the stars.There are several kinds of...

 () can be computed as:

Compare two proportional quantities, the free-fall time

Free-fall time

The free-fall time is the characteristic time that would take a body to collapse under its own gravitational attraction, if no other forces existed to oppose the collapse...

 (time to fall to a point mass from rest)
(17.7 % of the orbital period in a circular orbit)

and the time to fall to a point mass in a radial parabolic orbit
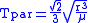(7.5 % of the orbital period in a circular orbit)

The fact that the formulas only differ by a constant factor is a priori clear from dimensional analysis

Dimensional analysis

In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...

.

Energy

The specific orbital energy

Specific orbital energy

In the gravitational two-body problem, the specific orbital energy \epsilon\,\! of two orbiting bodies is the constant sum of their mutual potential energy and their total kinetic energy , divided by the reduced mass...

 () is negative, and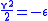

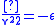
Thus the virial theorem applies even without taking a time-average:

• the kinetic energy of the system is equal to the absolute value of the total energy
• the potential energy of the system is equal to twice the total energy

The escape velocity

Escape velocity

In physics, escape velocity is the speed at which the kinetic energy plus the gravitational potential energy of an object is zero gravitational potential energy is negative since gravity is an attractive force and the potential is defined to be zero at infinity...

 from any distance is √2 times the speed in a circular orbit at that distance: the kinetic energy is twice as much, hence the total energy is zero.

Delta-v to reach a circular orbit

Maneuvering into a large circular orbit, e.g. a geostationary orbit

Geostationary orbit

A geostationary orbit is a geosynchronous orbit directly above the Earth's equator , with a period equal to the Earth's rotational period and an orbital eccentricity of approximately zero. An object in a geostationary orbit appears motionless, at a fixed position in the sky, to ground observers...

, requires a larger delta-v

Delta-v

In astrodynamics a Δv or delta-v is a scalar which takes units of speed. It is a measure of the amount of "effort" that is needed to change from one trajectory to another by making an orbital maneuver....

 than an escape orbit, although the latter implies getting arbitrarily far away and having more energy than needed for the orbital speed

Orbital speed

The orbital speed of a body, generally a planet, a natural satellite, an artificial satellite, or a multiple star, is the speed at which it orbits around the barycenter of a system, usually around a more massive body...

 of the circular orbit. It is also a matter of maneuvering into the orbit. See also Hohmann transfer orbit

Hohmann transfer orbit

In orbital mechanics, the Hohmann transfer orbit is an elliptical orbit used to transfer between two circular orbits, typically both in the same plane....

.

See also

• Elliptic orbit
  Elliptic orbit
  In astrodynamics or celestial mechanics an elliptic orbit is a Kepler orbit with the eccentricity less than 1; this includes the special case of a circular orbit, with eccentricity equal to zero. In a stricter sense, it is a Kepler orbit with the eccentricity greater than 0 and less than 1 . In a...
  
  
• List of orbits
• Two-body problem
  Two-body problem
  In classical mechanics, the two-body problem is to determine the motion of two point particles that interact only with each other. Common examples include a satellite orbiting a planet, a planet orbiting a star, two stars orbiting each other , and a classical electron orbiting an atomic nucleus In...