
Roche limit
Encyclopedia
The Roche limit sometimes referred to as the Roche radius, is the distance within which a celestial body, held together only by its own gravity, will disintegrate due to a second celestial body's tidal force
s exceeding the first body's gravitational self-attraction. Inside the Roche limit, orbiting
material will tend to disperse and form rings, while outside the limit, material will tend to coalesce
. The term is named after Édouard Roche
, the French
astronomer
who first calculated this theoretical limit in 1848.
disintegrating due to tidal forces induced by its primary, the body about which it orbit
s. Parts of the satellite that are closer to the primary are attracted by stronger gravity from the primary, whereas parts further away are repelled by stronger centrifugal force
from the satellite's curved orbit. Some real satellites, both natural
and artificial, can orbit within their Roche limits because they are held together by forces other than gravitation. Jupiter
's moon Metis
and Saturn
's moon Pan
are examples of such satellites, which hold together because of their tensile strength
(that is, they are solid and not easily pulled apart). In extreme cases, objects resting on the surface of such a satellite could actually be lifted away by tidal forces. A weaker satellite, such as a comet
, could be broken up when it passes within its Roche limit.
Since tidal forces overwhelm the gravity that might hold the satellite together within the Roche limit, no large satellite can gravitationally coalesce out of smaller particles within that limit. Indeed, almost all known planetary ring
s are located within their Roche limit, Saturn's E-Ring and Phoebe ring being notable exceptions. They could either be remnants from the planet's proto-planetary accretion disc
that failed to coalesce into moonlets, or conversely have formed when a moon passed within its Roche limit and broke apart.
It is also worth considering that the Roche limit is not the only factor that causes comets to break apart. Splitting by thermal stress, internal gas pressure and rotational splitting are a more likely way for a comet to split under stress.
shape while being held together only by its own self-gravity. Other effects are also neglected, such as tidal deformation of the primary, rotation and orbit of the satellite, and its irregular shape. These assumptions, although unrealistic, greatly simplify the Roche limit calculation.
The Roche limit for a rigid spherical satellite excluding orbital effects, is the distance,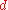 , from the primary at which the gravitational force on a test mass on the surface of the object is exactly equal to the tidal force pulling the object away from the object:
, from the primary at which the gravitational force on a test mass on the surface of the object is exactly equal to the tidal force pulling the object away from the object:
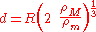 ,
,
where is the radius
is the radius
of the primary, is the density
is the density
of the primary, and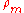 is the density of the satellite. Note that this does not depend on how large the orbiting object is, but only on the ratio of densities. This is the orbital distance inside of which loose material (e.g., regolith
is the density of the satellite. Note that this does not depend on how large the orbiting object is, but only on the ratio of densities. This is the orbital distance inside of which loose material (e.g., regolith
or loose rocks) on the surface of the satellite closest to the primary would be pulled away, and likewise material on the side opposite the primary will also be pulled away from, rather than toward, the satellite.
If the satellite is more than twice as dense as the primary, as can easily be the case for a rocky moon orbiting a gas giant, then the Roche limit will be inside the primary and hence not relevant.
.svg.png) In order to determine the Roche limit, we consider a small mass
In order to determine the Roche limit, we consider a small mass  on the surface of the satellite closest to the primary. There are two forces on this mass
on the surface of the satellite closest to the primary. There are two forces on this mass  : the gravitational pull towards the satellite and the gravitational pull towards the primary. Assuming that the satellite is in free fall
: the gravitational pull towards the satellite and the gravitational pull towards the primary. Assuming that the satellite is in free fall
around the primary and that the tidal force
is the only relevant term of the gravitational attraction of the primary. This assumption is a simplification as free-fall only truly applies to the planetary center, but will suffice for this derivation.
The gravitational pull on the mass
on the mass  towards the satellite with mass
towards the satellite with mass  and radius
and radius  can be expressed according to Newton's law of gravitation.
can be expressed according to Newton's law of gravitation.
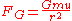
the tidal force
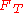 on the mass
on the mass  towards the primary with radius
towards the primary with radius  and mass
and mass  , at a distance
, at a distance  between the centers of the two bodies, can be expressed approximately as
between the centers of the two bodies, can be expressed approximately as
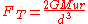 .
.
To obtain this approximation, find the difference in the primary's gravitational pull on the center of the satellite and on the edge of the satellite closest to the primary:
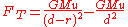
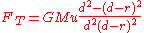
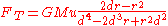
In the approximation where r< in the numerator and every term with  in the denominator goes to zero, which gives us:
in the denominator goes to zero, which gives us:
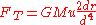

The Roche limit is reached when the gravitational force and the tidal force balance each other out.
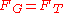
or
 ,
,
which gives the Roche limit,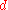 , as
, as
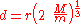 .
.
However, we don't really want the radius of the satellite to appear in the expression for the limit, so we re-write this in terms of densities.
For a sphere the mass can be written as
can be written as
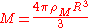 where
where  is the radius of the primary.
is the radius of the primary.
And likewise
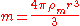 where
where  is the radius of the satellite.
is the radius of the satellite.
Substituting for the masses in the equation for the Roche limit, and cancelling out gives
gives
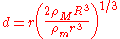 ,
,
which can be simplified to the Roche limit:
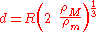 .
.
liquid satellite orbiting a planet, where any force acting upon the satellite would deform it into a prolate spheroid
.
The calculation is complex and its result cannot be represented in an exact algebraic formula. Roche himself derived the following approximate solution for the Roche Limit:
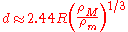
However, a better approximation that takes into account the primary's oblateness and the satellite's mass is:
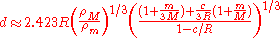
where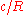 is the oblateness of the primary. The numerical factor is calculated with the aid of a computer.
is the oblateness of the primary. The numerical factor is calculated with the aid of a computer.
The fluid solution is appropriate for bodies that are only loosely held together, such as a comet. For instance, comet Shoemaker-Levy 9
's decaying orbit around Jupiter passed within its Roche limit in July 1992, causing it to fragment into a number of smaller pieces. On its next approach in 1994 the fragments crashed into the planet. Shoemaker-Levy 9 was first observed in 1993, but its orbit indicated that it had been captured by Jupiter a few decades prior. http://www.seds.org/sl9/landis.html
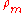 and volume
and volume  that do not depend on external or internal forces.
that do not depend on external or internal forces.
Second, assume the satellite moves in a circular orbit and it remains in synchronous rotation
. This means that the angular speed at which it rotates around its center of mass is the same as the angular speed at which it moves around the overall system barycenter
at which it rotates around its center of mass is the same as the angular speed at which it moves around the overall system barycenter
.
The angular speed is given by Kepler's third law:
is given by Kepler's third law:

When M is very much bigger than m, this will be close to
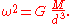
The synchronous rotation implies that the liquid does not move and the problem can be regarded as a static one. Therefore, the viscosity
and friction
of the liquid in this model do not play a role, since these quantities would play a role only for a moving fluid.
Given these assumptions, the following forces should be taken into account:
Since all of these forces are conservative, they can be expressed by means of a potential. Moreover, the surface of the satellite is an equipotential one. Otherwise, the differences of potential would give rise to forces and movement of some parts of the liquid at the surface, which contradicts the static model assumption. Given the distance from the main body, our problem is to determine the form of the surface that satisfies the equipotential condition.
 As the orbit has been assumed circular, the total gravitational force and centrifugal force acting on the main body cancel. Therefore, the force that affects the particles of the liquid is the tidal force, which depends on the position with respect to the center of mass, already considered in the rigid model. For small bodies, the distance of the liquid particles from the center of the body is small in relation to the distance d to the main body. Thus the tidal force can be linearized, resulting in the same formula for FT as given above.
As the orbit has been assumed circular, the total gravitational force and centrifugal force acting on the main body cancel. Therefore, the force that affects the particles of the liquid is the tidal force, which depends on the position with respect to the center of mass, already considered in the rigid model. For small bodies, the distance of the liquid particles from the center of the body is small in relation to the distance d to the main body. Thus the tidal force can be linearized, resulting in the same formula for FT as given above.
While this force in the rigid model depends only on the radius r of the satellite, in the fluid case we need to consider all the points on the surface and the tidal force depends on the distance Δd from the center of mass to a given particle projected on the line joining the satellite and the main body. We call Δd the radial distance. Since the tidal force is linear in Δd, the related potential is proportional to the square of the variable and for we have
we have
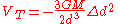
We want to determine the shape of the satellite for which the sum of the self-gravitation potential and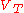 is constant on the surface of the body. In general, such a problem is very difficult to solve, but in this particular case, it can be solved by a skillful guess due to the square dependence of the tidal potential on the radial distance Δd
is constant on the surface of the body. In general, such a problem is very difficult to solve, but in this particular case, it can be solved by a skillful guess due to the square dependence of the tidal potential on the radial distance Δd
Since the potential VT changes only in one direction, i.e. the direction toward the main body, the satellite can be expected to take an axially symmetric form. More precisely, we may assume that it takes a form of a solid of revolution
. The self-potential on the surface of such a solid of revolution can only depend on the radial distance to the center of mass. Indeed, the intersection of the satellite and a plane perpendicular to the line joining the bodies is a disc whose boundary by our assumptions is a circle of constant potential. Should the difference between the self-gravitation potential and VT be constant, both potentials must depend in the same way on Δd. In other words, the self-potential has to be proportional to the square of Δd. Then it can be shown that the equipotential solution is an ellipsoid of revolution. Given a constant density and volume the self-potential of such body depends only on the eccentricity
ε of the ellipsoid:
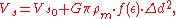
where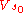 is the constant self-potential on the intersection of the circular edge of the body and the central symmetry plane given by the equation Δd=0.
is the constant self-potential on the intersection of the circular edge of the body and the central symmetry plane given by the equation Δd=0.
The dimensionless function f is to be determined from the accurate solution for the potential of the ellipsoid

and, surprisingly enough, does not depend on the volume of the satellite.
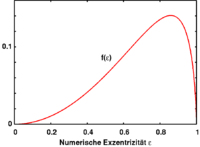 Although the explicit form of the function f looks complicated, it is clear
Although the explicit form of the function f looks complicated, it is clear
that we may and do choose the value of ε so that the potential VT is equal to VS plus a constant independent of the variable Δd. By inspection, this occurs when
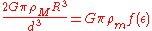
This equation can be solved numerically. The graph indicates that there are two solutions and thus the smaller one represents the stable equilibrium form (the ellipsoid with the smaller eccentricity). This solution determines the eccentricity of the tidal ellipsoid as a function of the distance to the main body. The derivative of the function f has a zero where the maximal eccentricity is attained. This corresponds to the Roche limit.
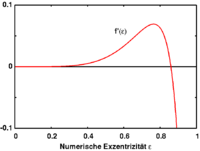 More precisely, the Roche limit is determined by the fact that the function f, which can be regarded as a nonlinear measure of the force squeezing the ellipsoid towards a spherical shape, is bounded so that there is an eccentricity at which this contracting force becomes maximal. Since the tidal force increases when the satellite approaches the main body, it is clear that there is a critical distance at which the ellipsoid is torn up.
More precisely, the Roche limit is determined by the fact that the function f, which can be regarded as a nonlinear measure of the force squeezing the ellipsoid towards a spherical shape, is bounded so that there is an eccentricity at which this contracting force becomes maximal. Since the tidal force increases when the satellite approaches the main body, it is clear that there is a critical distance at which the ellipsoid is torn up.
The maximal eccentricity can be calculated numerically as the zero of the derivative of f. One obtains
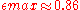
which corresponds to the ratio of the ellipsoid axes 1:1.95. Inserting this into the formula for the function f one can determine the minimal distance at which the ellipsoid exists. This is the Roche limit,

.
Using these data, the Roche Limits for rigid and fluid bodies can easily be calculated. The average density of comet
s is taken to be around 500 kg/m³.
The table below gives the Roche limits expressed in metres and in primary radii. The true Roche Limit for a satellite depends on its density and rigidity.
If the primary is less than half as dense as the satellite, the rigid-body Roche Limit is less than the primary's radius, and the two bodies may collide before the Roche limit is reached.
How close are the solar system's moons to their Roche limits? The table below gives each inner satellite's orbital radius divided by its own Roche radius. Both rigid and fluid body calculations are given. Note Pan
, Metis
, and Naiad
in particular, which may be quite close to their actual break-up points.
In practice, the densities of most of the inner satellites of giant planets are not known. In these cases, shown in italics, likely values have been assumed, but their actual Roche limit can vary from the value shown.
Tidal force
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
s exceeding the first body's gravitational self-attraction. Inside the Roche limit, orbiting
Planetary orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
material will tend to disperse and form rings, while outside the limit, material will tend to coalesce
Coalescence (meteorology)
Coalescence is the process by which two or more droplets, bubbles or particles merge during contact to form a single daughter droplet, bubble or particle. It can take place in many processes, ranging from meteorology to astrophysics. For example, it is both inve formation of raindrops as well as...
. The term is named after Édouard Roche
Édouard Roche
Édouard Albert Roche was a French astronomer and mathematician, who is best known for his work in the field of celestial mechanics...
, the French
France
The French Republic , The French Republic , The French Republic , (commonly known as France , is a unitary semi-presidential republic in Western Europe with several overseas territories and islands located on other continents and in the Indian, Pacific, and Atlantic oceans. Metropolitan France...
astronomer
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
who first calculated this theoretical limit in 1848.
Explanation
Typically, the Roche limit applies to a satelliteSatellite
In the context of spaceflight, a satellite is an object which has been placed into orbit by human endeavour. Such objects are sometimes called artificial satellites to distinguish them from natural satellites such as the Moon....
disintegrating due to tidal forces induced by its primary, the body about which it orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s. Parts of the satellite that are closer to the primary are attracted by stronger gravity from the primary, whereas parts further away are repelled by stronger centrifugal force
Centrifugal force
Centrifugal force can generally be any force directed outward relative to some origin. More particularly, in classical mechanics, the centrifugal force is an outward force which arises when describing the motion of objects in a rotating reference frame...
from the satellite's curved orbit. Some real satellites, both natural
Natural satellite
A natural satellite or moon is a celestial body that orbits a planet or smaller body, which is called its primary. The two terms are used synonymously for non-artificial satellites of planets, of dwarf planets, and of minor planets....
and artificial, can orbit within their Roche limits because they are held together by forces other than gravitation. Jupiter
Jupiter
Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
's moon Metis
Metis (moon)
Metis , also known as ', is the innermost moon of Jupiter. It was discovered in 1979 in images taken by Voyager 1, and was named in 1983 after the first wife of Zeus, Metis...
and Saturn
Saturn
Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,...
's moon Pan
Pan (moon)
Pan is the innermost moon of Saturn. It is a walnut-shaped small moon about 35 kilometres across and 23 km high that orbits within the Encke Gap in Saturn's A Ring. Pan acts as a ring shepherd and is responsible for keeping the Encke Gap free of ring particles.It was discovered by Mark R...
are examples of such satellites, which hold together because of their tensile strength
Tensile strength
Ultimate tensile strength , often shortened to tensile strength or ultimate strength, is the maximum stress that a material can withstand while being stretched or pulled before necking, which is when the specimen's cross-section starts to significantly contract...
(that is, they are solid and not easily pulled apart). In extreme cases, objects resting on the surface of such a satellite could actually be lifted away by tidal forces. A weaker satellite, such as a comet
Comet
A comet is an icy small Solar System body that, when close enough to the Sun, displays a visible coma and sometimes also a tail. These phenomena are both due to the effects of solar radiation and the solar wind upon the nucleus of the comet...
, could be broken up when it passes within its Roche limit.
Since tidal forces overwhelm the gravity that might hold the satellite together within the Roche limit, no large satellite can gravitationally coalesce out of smaller particles within that limit. Indeed, almost all known planetary ring
Planetary ring
A planetary ring is a ring of cosmic dust and other small particles orbiting around a planet in a flat disc-shaped region.The most notable planetary rings known in Earth's solar system are those around Saturn, but the other three gas giants of the solar system possess ring systems of their...
s are located within their Roche limit, Saturn's E-Ring and Phoebe ring being notable exceptions. They could either be remnants from the planet's proto-planetary accretion disc
Accretion disc
An accretion disc is a structure formed by diffuse material in orbital motion around a central body. The central body is typically a star. Gravity causes material in the disc to spiral inward towards the central body. Gravitational forces compress the material causing the emission of...
that failed to coalesce into moonlets, or conversely have formed when a moon passed within its Roche limit and broke apart.
It is also worth considering that the Roche limit is not the only factor that causes comets to break apart. Splitting by thermal stress, internal gas pressure and rotational splitting are a more likely way for a comet to split under stress.
Determining the Roche limit
The limiting distance to which a satellite can approach without breaking up depends on the rigidity of the satellite. At one extreme, a completely rigid satellite will maintain its shape until tidal forces break it apart. At the other extreme, a highly fluid satellite gradually deforms leading to increased tidal forces, causing the satellite to elongate, further compounding the tidal forces and causing it to break apart more readily. Most real satellites would lie somewhere between these two extremes, with tensile strength rendering the satellite neither perfectly rigid nor perfectly fluid. The Roche limit is also usually calculated for the case of a circular orbit, although it is straightforward to modify the calculation to apply to the case (for example) of a body passing the primary on a parabolic or hyperbolic trajectory.Rigid satellite calculation
The rigid body Roche limit is a simplified calculation for a spherical satellite, where the deformation of the body by tidal effects is neglected. The body is assumed to maintain its sphericalSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
shape while being held together only by its own self-gravity. Other effects are also neglected, such as tidal deformation of the primary, rotation and orbit of the satellite, and its irregular shape. These assumptions, although unrealistic, greatly simplify the Roche limit calculation.
The Roche limit for a rigid spherical satellite excluding orbital effects, is the distance,
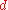 , from the primary at which the gravitational force on a test mass on the surface of the object is exactly equal to the tidal force pulling the object away from the object:
, from the primary at which the gravitational force on a test mass on the surface of the object is exactly equal to the tidal force pulling the object away from the object: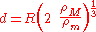 ,
,where
 is the radius
is the radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the primary,
 is the density
is the densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
of the primary, and
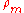 is the density of the satellite. Note that this does not depend on how large the orbiting object is, but only on the ratio of densities. This is the orbital distance inside of which loose material (e.g., regolith
is the density of the satellite. Note that this does not depend on how large the orbiting object is, but only on the ratio of densities. This is the orbital distance inside of which loose material (e.g., regolithRegolith
Regolith is a layer of loose, heterogeneous material covering solid rock. It includes dust, soil, broken rock, and other related materials and is present on Earth, the Moon, some asteroids, and other terrestrial planets and moons.-Etymology:...
or loose rocks) on the surface of the satellite closest to the primary would be pulled away, and likewise material on the side opposite the primary will also be pulled away from, rather than toward, the satellite.
If the satellite is more than twice as dense as the primary, as can easily be the case for a rocky moon orbiting a gas giant, then the Roche limit will be inside the primary and hence not relevant.
Derivation of the formula
.svg.png)
 on the surface of the satellite closest to the primary. There are two forces on this mass
on the surface of the satellite closest to the primary. There are two forces on this mass  : the gravitational pull towards the satellite and the gravitational pull towards the primary. Assuming that the satellite is in free fall
: the gravitational pull towards the satellite and the gravitational pull towards the primary. Assuming that the satellite is in free fallFree fall
Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...
around the primary and that the tidal force
Tidal force
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
is the only relevant term of the gravitational attraction of the primary. This assumption is a simplification as free-fall only truly applies to the planetary center, but will suffice for this derivation.
The gravitational pull
 on the mass
on the mass  towards the satellite with mass
towards the satellite with mass  and radius
and radius  can be expressed according to Newton's law of gravitation.
can be expressed according to Newton's law of gravitation.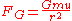
the tidal force
Tidal force
The tidal force is a secondary effect of the force of gravity and is responsible for the tides. It arises because the gravitational force per unit mass exerted on one body by a second body is not constant across its diameter, the side nearest to the second being more attracted by it than the side...
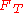 on the mass
on the mass  towards the primary with radius
towards the primary with radius  and mass
and mass  , at a distance
, at a distance  between the centers of the two bodies, can be expressed approximately as
between the centers of the two bodies, can be expressed approximately as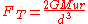 .
.To obtain this approximation, find the difference in the primary's gravitational pull on the center of the satellite and on the edge of the satellite closest to the primary:
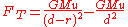
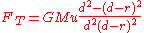
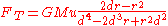
In the approximation where r<
 in the denominator goes to zero, which gives us:
in the denominator goes to zero, which gives us: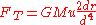

The Roche limit is reached when the gravitational force and the tidal force balance each other out.
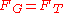
or
 ,
,which gives the Roche limit,
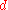 , as
, as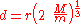 .
.However, we don't really want the radius of the satellite to appear in the expression for the limit, so we re-write this in terms of densities.
For a sphere the mass
 can be written as
can be written as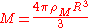 where
where  is the radius of the primary.
is the radius of the primary.And likewise
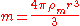 where
where  is the radius of the satellite.
is the radius of the satellite.Substituting for the masses in the equation for the Roche limit, and cancelling out
 gives
gives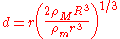 ,
,which can be simplified to the Roche limit:
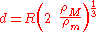 .
.Fluid satellites
A more accurate approach for calculating the Roche Limit takes the deformation of the satellite into account. An extreme example would be a tidally lockedTidal locking
Tidal locking occurs when the gravitational gradient makes one side of an astronomical body always face another; for example, the same side of the Earth's Moon always faces the Earth. A tidally locked body takes just as long to rotate around its own axis as it does to revolve around its partner...
liquid satellite orbiting a planet, where any force acting upon the satellite would deform it into a prolate spheroid
Spheroid
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....
.
The calculation is complex and its result cannot be represented in an exact algebraic formula. Roche himself derived the following approximate solution for the Roche Limit:
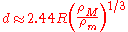
However, a better approximation that takes into account the primary's oblateness and the satellite's mass is:
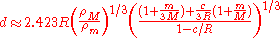
where
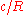 is the oblateness of the primary. The numerical factor is calculated with the aid of a computer.
is the oblateness of the primary. The numerical factor is calculated with the aid of a computer.The fluid solution is appropriate for bodies that are only loosely held together, such as a comet. For instance, comet Shoemaker-Levy 9
Comet Shoemaker-Levy 9
Comet Shoemaker–Levy 9 was a comet that broke apart and collided with Jupiter in July 1994, providing the first direct observation of an extraterrestrial collision of solar system objects. This generated a large amount of coverage in the popular media, and the comet was closely observed by...
's decaying orbit around Jupiter passed within its Roche limit in July 1992, causing it to fragment into a number of smaller pieces. On its next approach in 1994 the fragments crashed into the planet. Shoemaker-Levy 9 was first observed in 1993, but its orbit indicated that it had been captured by Jupiter a few decades prior. http://www.seds.org/sl9/landis.html
Derivation of the formula
As the fluid satellite case is more delicate than the rigid one, the satellite is described with some simplifying assumptions. First, assume the object consists of incompressible fluid that has constant density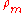 and volume
and volume  that do not depend on external or internal forces.
that do not depend on external or internal forces.Second, assume the satellite moves in a circular orbit and it remains in synchronous rotation
Synchronous rotation
In astronomy, synchronous rotation is a planetological term describing a body orbiting another, where the orbiting body takes as long to rotate on its axis as it does to make one orbit; and therefore always keeps the same hemisphere pointed at the body it is orbiting...
. This means that the angular speed
 at which it rotates around its center of mass is the same as the angular speed at which it moves around the overall system barycenter
at which it rotates around its center of mass is the same as the angular speed at which it moves around the overall system barycenterBarycentric coordinates (astronomy)
In astronomy, barycentric coordinates are non-rotating coordinates with origin at the center of mass of two or more bodies.The barycenter is the point between two objects where they balance each other. For example, it is the center of mass where two or more celestial bodies orbit each other...
.
The angular speed
 is given by Kepler's third law:
is given by Kepler's third law:
When M is very much bigger than m, this will be close to
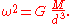
The synchronous rotation implies that the liquid does not move and the problem can be regarded as a static one. Therefore, the viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
and friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
of the liquid in this model do not play a role, since these quantities would play a role only for a moving fluid.
Given these assumptions, the following forces should be taken into account:
- The force of gravitation due to the main body;
- the centrifugal force in the rotary reference system; and
- the self-gravitation field of the satellite.
Since all of these forces are conservative, they can be expressed by means of a potential. Moreover, the surface of the satellite is an equipotential one. Otherwise, the differences of potential would give rise to forces and movement of some parts of the liquid at the surface, which contradicts the static model assumption. Given the distance from the main body, our problem is to determine the form of the surface that satisfies the equipotential condition.

While this force in the rigid model depends only on the radius r of the satellite, in the fluid case we need to consider all the points on the surface and the tidal force depends on the distance Δd from the center of mass to a given particle projected on the line joining the satellite and the main body. We call Δd the radial distance. Since the tidal force is linear in Δd, the related potential is proportional to the square of the variable and for
 we have
we have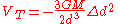
We want to determine the shape of the satellite for which the sum of the self-gravitation potential and
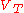 is constant on the surface of the body. In general, such a problem is very difficult to solve, but in this particular case, it can be solved by a skillful guess due to the square dependence of the tidal potential on the radial distance Δd
is constant on the surface of the body. In general, such a problem is very difficult to solve, but in this particular case, it can be solved by a skillful guess due to the square dependence of the tidal potential on the radial distance ΔdSince the potential VT changes only in one direction, i.e. the direction toward the main body, the satellite can be expected to take an axially symmetric form. More precisely, we may assume that it takes a form of a solid of revolution
Solid of revolution
In mathematics, engineering, and manufacturing, a solid of revolution is a solid figure obtained by rotating a plane curve around some straight line that lies on the same plane....
. The self-potential on the surface of such a solid of revolution can only depend on the radial distance to the center of mass. Indeed, the intersection of the satellite and a plane perpendicular to the line joining the bodies is a disc whose boundary by our assumptions is a circle of constant potential. Should the difference between the self-gravitation potential and VT be constant, both potentials must depend in the same way on Δd. In other words, the self-potential has to be proportional to the square of Δd. Then it can be shown that the equipotential solution is an ellipsoid of revolution. Given a constant density and volume the self-potential of such body depends only on the eccentricity
Eccentricity (mathematics)
In mathematics, the eccentricity, denoted e or \varepsilon, is a parameter associated with every conic section. It can be thought of as a measure of how much the conic section deviates from being circular.In particular,...
ε of the ellipsoid:
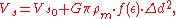
where
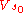 is the constant self-potential on the intersection of the circular edge of the body and the central symmetry plane given by the equation Δd=0.
is the constant self-potential on the intersection of the circular edge of the body and the central symmetry plane given by the equation Δd=0.The dimensionless function f is to be determined from the accurate solution for the potential of the ellipsoid

and, surprisingly enough, does not depend on the volume of the satellite.

that we may and do choose the value of ε so that the potential VT is equal to VS plus a constant independent of the variable Δd. By inspection, this occurs when
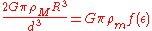
This equation can be solved numerically. The graph indicates that there are two solutions and thus the smaller one represents the stable equilibrium form (the ellipsoid with the smaller eccentricity). This solution determines the eccentricity of the tidal ellipsoid as a function of the distance to the main body. The derivative of the function f has a zero where the maximal eccentricity is attained. This corresponds to the Roche limit.

The maximal eccentricity can be calculated numerically as the zero of the derivative of f. One obtains
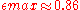
which corresponds to the ratio of the ellipsoid axes 1:1.95. Inserting this into the formula for the function f one can determine the minimal distance at which the ellipsoid exists. This is the Roche limit,

Roche limits for selected examples
The table below shows the mean density and the equatorial radius for selected objects in our solar systemSolar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
.
| Primary | Density (kg/m³) | Radius (m) |
|---|---|---|
| Sun Sun The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields... |
1,408 | 696,000,000 |
| Jupiter Jupiter Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,... |
1,326 | 71,492,000 |
| Earth Earth Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets... |
5,513 | 6,378,137 |
| Moon Moon The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more... |
3,346 | 1,738,100 |
| Saturn Saturn Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,... |
0,687 | 60,268,000 |
| Uranus Uranus Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus... |
1,318 | 25,559,000 |
| Neptune Neptune Neptune is the eighth and farthest planet from the Sun in the Solar System. Named for the Roman god of the sea, it is the fourth-largest planet by diameter and the third largest by mass. Neptune is 17 times the mass of Earth and is slightly more massive than its near-twin Uranus, which is 15 times... |
1,638 | 24,764,000 |
Using these data, the Roche Limits for rigid and fluid bodies can easily be calculated. The average density of comet
Comet
A comet is an icy small Solar System body that, when close enough to the Sun, displays a visible coma and sometimes also a tail. These phenomena are both due to the effects of solar radiation and the solar wind upon the nucleus of the comet...
s is taken to be around 500 kg/m³.
The table below gives the Roche limits expressed in metres and in primary radii. The true Roche Limit for a satellite depends on its density and rigidity.
| Body | Satellite | Roche limit (rigid) | Roche limit (fluid) | ||
|---|---|---|---|---|---|
| Distance (km) | R | Distance (km) | R | ||
| Earth | Moon | 9,496 | 1.49 | 18,261 | 2.86 |
| Earth | average Comet | 17,880 | 2.80 | 34,390 | 5.39 |
| Sun | Earth | 554,400 | 0.80 | 1,066,300 | 1.53 |
| Sun | Jupiter | 890,700 | 1.28 | 1,713,000 | 2.46 |
| Sun | Moon | 655,300 | 0.94 | 1,260,300 | 1.81 |
| Sun | average Comet | 1,234,000 | 1.78 | 2,374,000 | 3.42 |
If the primary is less than half as dense as the satellite, the rigid-body Roche Limit is less than the primary's radius, and the two bodies may collide before the Roche limit is reached.
How close are the solar system's moons to their Roche limits? The table below gives each inner satellite's orbital radius divided by its own Roche radius. Both rigid and fluid body calculations are given. Note Pan
Pan (moon)
Pan is the innermost moon of Saturn. It is a walnut-shaped small moon about 35 kilometres across and 23 km high that orbits within the Encke Gap in Saturn's A Ring. Pan acts as a ring shepherd and is responsible for keeping the Encke Gap free of ring particles.It was discovered by Mark R...
, Metis
Metis (moon)
Metis , also known as ', is the innermost moon of Jupiter. It was discovered in 1979 in images taken by Voyager 1, and was named in 1983 after the first wife of Zeus, Metis...
, and Naiad
Naiad (moon)
Naiad , also known as Neptune III, is the innermost satellite of Neptune, named after the Naiads of Greek legend.Naiad was discovered sometime before mid-September 1989 from the images taken by the Voyager 2 probe. The last moon to be discovered during the flyby, it was designated...
in particular, which may be quite close to their actual break-up points.
In practice, the densities of most of the inner satellites of giant planets are not known. In these cases, shown in italics, likely values have been assumed, but their actual Roche limit can vary from the value shown.
| Primary | Satellite | Orbital Radius / Roche limit | |
|---|---|---|---|
| (rigid) | (fluid) | ||
| Sun Sun The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields... |
Mercury Mercury (planet) Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits... |
104:1 | 54:1 |
| Earth Earth Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets... |
Moon Moon The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more... |
41:1 | 21:1 |
| Mars Mars Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance... |
Phobos Phobos (moon) Phobos is the larger and closer of the two natural satellites of Mars. Both moons were discovered in 1877. With a mean radius of , Phobos is 7.24 times as massive as Deimos... |
172% | 89% |
| Deimos Deimos (moon) Deimos is the smaller and outer of Mars's two moons . It is named after Deimos, a figure representing dread in Greek Mythology. Its systematic designation is '.-Discovery:Deimos was discovered by Asaph Hall, Sr... |
451% | 234% | |
| Jupiter Jupiter Jupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,... |
Metis Metis (moon) Metis , also known as ', is the innermost moon of Jupiter. It was discovered in 1979 in images taken by Voyager 1, and was named in 1983 after the first wife of Zeus, Metis... |
~186% | ~94% |
| Adrastea Adrastea (moon) Adrastea , also known as ', is the second by distance, and the smallest of the four inner moons of Jupiter. It was discovered in Voyager 2 probe photographs taken in 1979, making it the first natural satellite to be discovered from images taken by an interplanetary spacecraft, rather than... |
~188% | ~95% | |
| Amalthea Amalthea (moon) Amalthea is the third moon of Jupiter in order of distance from the planet. It was discovered on September 9, 1892, by Edward Emerson Barnard and named after Amalthea, a nymph in Greek mythology. It is also known as '.... |
175% | 88% | |
| Thebe Thebe (moon) Thebe also known as ', is the fourth of Jupiter's moons by distance from the planet. It was discovered by Stephen P. Synnott in images from the Voyager 1 space probe taken on March 5, 1979, while orbiting around Jupiter... |
254% | 128% | |
| Saturn Saturn Saturn is the sixth planet from the Sun and the second largest planet in the Solar System, after Jupiter. Saturn is named after the Roman god Saturn, equated to the Greek Cronus , the Babylonian Ninurta and the Hindu Shani. Saturn's astronomical symbol represents the Roman god's sickle.Saturn,... |
Pan Pan (moon) Pan is the innermost moon of Saturn. It is a walnut-shaped small moon about 35 kilometres across and 23 km high that orbits within the Encke Gap in Saturn's A Ring. Pan acts as a ring shepherd and is responsible for keeping the Encke Gap free of ring particles.It was discovered by Mark R... |
142% | 70% |
| Atlas Atlas (moon) Atlas is an inner satellite of Saturn.Atlas was discovered by Richard Terrile in 1980 from Voyager photos and was designated '. In 1983 it was officially named after Atlas of Greek mythology, because it "holds the rings on its shoulders" like the Titan Atlas held the sky up above the Earth... |
156% | 78% | |
| Prometheus Prometheus (moon) -Animations:-External links:* at ** anaglyph view of Prometheus... |
162% | 80% | |
| Pandora Pandora (moon) Pandora is an inner satellite of Saturn. It was discovered in 1980 from photos taken by the Voyager 1 probe, and was provisionally designated '. In late 1985 it was officially named after Pandora from Greek mythology. It is also designated as '.Pandora is the outer shepherd satellite of the F Ring... |
167% | 83% | |
| Epimetheus Epimetheus (moon) Epimetheus is an inner satellite of Saturn. It is also known as Saturn XI. It is named after the mythological Epimetheus, brother of Prometheus.-Discovery:Epimetheus occupies essentially the same orbit as the moon Janus... |
200% | 99% | |
| Janus Janus (moon) Janus is an inner satellite of Saturn. It is also known as Saturn X . It is named after the mythological Janus.-Discovery and orbit:Janus occupies practically the same orbit as the moon Epimetheus... |
195% | 97% | |
| Uranus Uranus Uranus is the seventh planet from the Sun. It has the third-largest planetary radius and fourth-largest planetary mass in the Solar System. It is named after the ancient Greek deity of the sky Uranus , the father of Cronus and grandfather of Zeus... |
Cordelia Cordelia (moon) Cordelia is the innermost moon of Uranus. It was discovered from the images taken by Voyager 2 on January 20, 1986, and was given the temporary designation S/1986 U 7. It was not detected again until the Hubble Space Telescope observed it in 1997... |
~154% | ~79% |
| Ophelia Ophelia (moon) Ophelia is a moon of Uranus. It was discovered from the images taken by Voyager 2 on January 20, 1986, and was given the temporary designation S/1986 U 8. It was not seen until the Hubble Space Telescope recovered it in 2003. Ophelia was named after the daughter of Polonius, Ophelia, in... |
~166% | ~86% | |
| Bianca Bianca (moon) Bianca is an inner satellite of Uranus. It was discovered from the images taken by Voyager 2 on January 23, 1986, and was given the temporary designation S/1986 U 9. It was named after the sister of Katherine in Shakespeare's play The Taming of the Shrew... |
~183% | ~94% | |
| Cressida Cressida (moon) Cressida is an inner satellite of Uranus. It was discovered from the images taken by Voyager 2 on 9 January 1986, and was given the temporary designation S/1986 U 3. It was named after the Trojan daughter of Calchas, a tragic heroine who appears in William Shakespeare's play Troilus and... |
~191% | ~98% | |
| Desdemona Desdemona (moon) Desdemona is an inner satellite of Uranus. It was discovered from the images taken by Voyager 2 on 13 January 1986, and was given the temporary designation S/1986 U 6. Desdemona is named after the wife of Othello in William Shakespeare's play Othello... |
~194% | ~100% | |
| Juliet Juliet (moon) Juliet is an inner satellite of Uranus. It was discovered from the images taken by Voyager 2 on 3 January 1986, and was given the temporary designation S/1986 U 2. It is named after the heroine of William Shakespeare's play Romeo and Juliet... |
~199% | ~102% | |
| Neptune Neptune Neptune is the eighth and farthest planet from the Sun in the Solar System. Named for the Roman god of the sea, it is the fourth-largest planet by diameter and the third largest by mass. Neptune is 17 times the mass of Earth and is slightly more massive than its near-twin Uranus, which is 15 times... |
Naiad Naiad (moon) Naiad , also known as Neptune III, is the innermost satellite of Neptune, named after the Naiads of Greek legend.Naiad was discovered sometime before mid-September 1989 from the images taken by the Voyager 2 probe. The last moon to be discovered during the flyby, it was designated... |
~139% | ~72% |
| Thalassa Thalassa (moon) Thalassa , also known as Neptune IV, is the second innermost satellite of Neptune. Thalassa was named after sea goddesss Thalassa, a daughter of Aether and Hemera from Greek mythology. "Thalassa" is also the Greek word for "sea".... |
~145% | ~75% | |
| Despina Despina (moon) Despina , also known as Neptune V, is the third closest inner satellite of Neptune. It is named after Despoina, a nymph who was a daughter of Poseidon and Demeter.... |
~152% | ~78% | |
| Galatea Galatea (moon) Galatea , also known as Neptune VI, is the fourth closest inner satellite of Neptune. It is named after Galatea, one of the Nereids of Greek legend.Galatea was discovered in late July 1989 from the images taken by the Voyager 2 probe... |
153% | 79% | |
| Larissa Larissa (moon) Larissa , also known as Neptune VII, is the fifth-closest inner satellite of Neptune. It is named after Larissa, a lover of Poseidon in Greek mythology and eponymous nymph of the city in Thessaly.- Discovery :... |
~218% | ~113% | |
| Pluto Pluto Pluto, formal designation 134340 Pluto, is the second-most-massive known dwarf planet in the Solar System and the tenth-most-massive body observed directly orbiting the Sun... |
Charon Charon (moon) Charon is the largest satellite of the dwarf planet Pluto. It was discovered in 1978 at the United States Naval Observatory Flagstaff Station. Following the 2005 discovery of two other natural satellites of Pluto , Charon may also be referred to as Pluto I... |
12.5:1 | 6.5:1 |
See also
- Roche lobeRoche lobeThe Roche lobe is the region of space around a star in a binary system within which orbiting material is gravitationally bound to that star. If the star expands past its Roche lobe, then the material can escape the gravitational pull of the star. If the star is in a binary system then the material...
- Chandrasekhar limitChandrasekhar limitWhen a star starts running out of fuel, it usually cools off and collapses into one of three compact forms, depending on its total mass:* a White Dwarf, a big lump of Carbon and Oxygen atoms, almost like one huge molecule...
- Hill sphereHill sphereAn astronomical body's Hill sphere is the region in which it dominates the attraction of satellites. To be retained by a planet, a moon must have an orbit that lies within the planet's Hill sphere. That moon would, in turn, have a Hill sphere of its own...
- SpaghettificationSpaghettificationIn astrophysics, spaghettification is the vertical stretching and horizontal compression of objects into long thin shapes in a very strong gravitational field, and is caused by extreme tidal forces...
(a rather extreme tidal distortion) - Black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
- Triton (moon)Triton (moon)Triton is the largest moon of the planet Neptune, discovered on October 10, 1846, by English astronomer William Lassell. It is the only large moon in the Solar System with a retrograde orbit, which is an orbit in the opposite direction to its planet's rotation. At 2,700 km in diameter, it is...
(Neptune satellite) - Comet Shoemaker–Levy 9
Other uses
- Roche Limit is the name of a Canadian Electronic pop band.
Sources
- Édouard Roche: "La figure d'une masse fluide soumise à l'attraction d'un point éloigné" (The figure of a fluid mass subjected to the attraction of a distant point), part 1, Académie des sciences de Montpellier: Mémoires de la section des sciences, Volume 1 (1849) 243–262. 2.44 is mentioned on page 258.
- Édouard Roche: "La figure d'une masse fluide soumise à l'attraction d'un point éloigné", part 2, Académie des sciences de Montpellier: Mémoires de la section des sciences, Volume 1 (1850) 333–348.
- Édouard Roche: "La figure d'une masse fluide soumise à l'attraction d'un point éloigné", part 3, Académie des sciences de Montpellier: Mémoires de la section des sciences, Volume 2 (1851) 21–32.
- George Howard Darwin, "On the figure and stability of a liquid satellite", Scientific Papers, Volume 3 (1910) 436–524.
- James Hopwood Jeans, Problems of cosmogony and stellar dynamics, Chapter III: Ellipsoidal configurations of equilibrium, 1919.
- S. Chandrasekhar, Ellipsoidal figures of equilibrium (New Haven: Yale University Press, 1969), Chapter 8: The Roche ellipsoids (189–240).
- S. Chandrasekhar, "The equilibrium and the stability of the Roche ellipsoids", Astrophysical Journal 138 (1963) 1182–1213.
External links
- Discussion of the Roche Limit
- Audio: Cain/Gay - Astronomy Cast Tidal Forces Across the Universe - July 2007.

