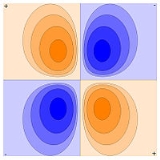
Quadrupole
Overview
Multipole expansion
A multipole expansion is a mathematical series representing a function that depends on angles — usually the two angles on a sphere. These series are useful because they can often be truncated, meaning that only the first few terms need to be retained for a good approximation to the original...
of a more complex structure reflecting various orders of complexity.
The zero-trace quadrupole moment tensor of a system of charges (or masses, for example) is defined as
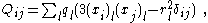
for a discrete system with individual charges
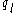 , or
, or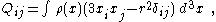
for a continuous system with charge density
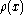 .
.
Unanswered Questions

