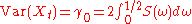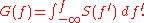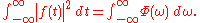Spectral density
Encyclopedia
In statistical signal processing
and physics
, the spectral density, power spectral density (PSD), or energy spectral density (ESD), is a positive real function of a frequency variable associated with a stationary stochastic process
, or a deterministic function of time, which has dimensions of power per hertz
(Hz), or energy per hertz. It is often called simply the spectrum
of the signal. Intuitively, the spectral density measures the frequency content of a stochastic process
and helps identify periodicities.
, the signal is usually a wave, such as an electromagnetic wave, random vibration
, or an acoustic wave. The spectral density of the wave, when multiplied by an appropriate factor, will give the power
carried by the wave, per unit frequency, known as the power spectral density (PSD) of the signal. Power spectral density is commonly expressed in watt
s per hertz
(W/Hz) or dBm
/Hz.
For voltage
signals, it is customary to use units of V2Hz−1 for PSD, and V2sHz−1 for ESD or dBμV/Hz.
For random vibration analysis, units of g
2Hz−1 are sometimes used for acceleration
spectral density.
Although it is not necessary to assign physical dimensions to the signal or its argument, in the following discussion the terms used will assume that the signal varies in time.
is distributed with frequency. If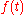 is a finite-energy (square integrable) signal, the spectral density
is a finite-energy (square integrable) signal, the spectral density 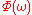 of the signal is the square of the magnitude of the continuous Fourier transform
of the signal is the square of the magnitude of the continuous Fourier transform
of the signal (here energy is taken as the integral of the square of a signal, which is the same as physical energy if the signal is a voltage applied to a 1-ohm load, or the current
).

where is the angular frequency
is the angular frequency
( times the ordinary frequency) and
times the ordinary frequency) and  is the continuous Fourier transform
is the continuous Fourier transform
of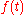 , and
, and  is its complex conjugate
is its complex conjugate
.
If the signal is discrete with values , over an infinite number of elements, we still have an energy spectral density:
, over an infinite number of elements, we still have an energy spectral density:

where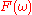 is the discrete-time Fourier transform
is the discrete-time Fourier transform
of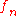 .
.
If the number of defined values is finite, the sequence does not have an energy spectral density per se, but the sequence can be treated as periodic, using a Discrete Fourier Transform
(DFT) to make a discrete spectrum, or it can be extended with zeros and a spectral density can be computed as in the infinite-sequence case.
The continuous and discrete spectral densities are often denoted with the same symbols, as above, though their dimensions and units differ; the continuous case has a time-squared factor that the discrete case does not have. They can be made to have equal dimensions and units by measuring time in units of sample intervals or by scaling the discrete case to the desired time units.
As is always the case, the multiplicative factor of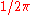 is not absolute, but rather depends on the particular normalizing constants used in the definition of the various Fourier transforms.
is not absolute, but rather depends on the particular normalizing constants used in the definition of the various Fourier transforms.
.) An often more useful alternative is the power spectral density (PSD), which describes how the power
of a signal or time series is distributed with frequency. Here power can be the actual physical power, or more often, for convenience with abstract signals, can be defined as the squared value of the signal, that is, as the actual power dissipated in a purely resistive
load if the signal were a voltage
applied across it. This instantaneous power (the mean or expected value of which is the average power) is then given by
Statistical signal processing
Statistical signal processing is an area of Applied Mathematics and Signal Processing that treats signals as stochastic processes, dealing with their statistical properties...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the spectral density, power spectral density (PSD), or energy spectral density (ESD), is a positive real function of a frequency variable associated with a stationary stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
, or a deterministic function of time, which has dimensions of power per hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
(Hz), or energy per hertz. It is often called simply the spectrum
Spectrum
A spectrum is a condition that is not limited to a specific set of values but can vary infinitely within a continuum. The word saw its first scientific use within the field of optics to describe the rainbow of colors in visible light when separated using a prism; it has since been applied by...
of the signal. Intuitively, the spectral density measures the frequency content of a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
and helps identify periodicities.
Explanation
In physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, the signal is usually a wave, such as an electromagnetic wave, random vibration
Random vibration
In mechanical engineering, random vibration is motion which is non-deterministic, meaning that future behavior cannot be precisely predicted. The randomness is a characteristic of the excitation or input, not the mode shapes or natural frequencies...
, or an acoustic wave. The spectral density of the wave, when multiplied by an appropriate factor, will give the power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
carried by the wave, per unit frequency, known as the power spectral density (PSD) of the signal. Power spectral density is commonly expressed in watt
Watt
The watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
s per hertz
Hertz
The hertz is the SI unit of frequency defined as the number of cycles per second of a periodic phenomenon. One of its most common uses is the description of the sine wave, particularly those used in radio and audio applications....
(W/Hz) or dBm
DBm
dBm is an abbreviation for the power ratio in decibels of the measured power referenced to one milliwatt . It is used in radio, microwave and fiber optic networks as a convenient measure of absolute power because of its capability to express both very large and very small values in a short form...
/Hz.
For voltage
Voltage
Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
signals, it is customary to use units of V2Hz−1 for PSD, and V2sHz−1 for ESD or dBμV/Hz.
For random vibration analysis, units of g
G-force
The g-force associated with an object is its acceleration relative to free-fall. This acceleration experienced by an object is due to the vector sum of non-gravitational forces acting on an object free to move. The accelerations that are not produced by gravity are termed proper accelerations, and...
2Hz−1 are sometimes used for acceleration
Acceleration
In physics, acceleration is the rate of change of velocity with time. In one dimension, acceleration is the rate at which something speeds up or slows down. However, since velocity is a vector, acceleration describes the rate of change of both the magnitude and the direction of velocity. ...
spectral density.
Although it is not necessary to assign physical dimensions to the signal or its argument, in the following discussion the terms used will assume that the signal varies in time.
Energy spectral density
The energy spectral density describes how the energy (or variance) of a signal or a time seriesTime series
In statistics, signal processing, econometrics and mathematical finance, a time series is a sequence of data points, measured typically at successive times spaced at uniform time intervals. Examples of time series are the daily closing value of the Dow Jones index or the annual flow volume of the...
is distributed with frequency. If
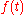 is a finite-energy (square integrable) signal, the spectral density
is a finite-energy (square integrable) signal, the spectral density 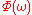 of the signal is the square of the magnitude of the continuous Fourier transform
of the signal is the square of the magnitude of the continuous Fourier transformContinuous Fourier transform
The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
of the signal (here energy is taken as the integral of the square of a signal, which is the same as physical energy if the signal is a voltage applied to a 1-ohm load, or the current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
).

where
 is the angular frequency
is the angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
(
 times the ordinary frequency) and
times the ordinary frequency) and  is the continuous Fourier transform
is the continuous Fourier transformContinuous Fourier transform
The Fourier transform is a mathematical operation that decomposes a function into its constituent frequencies, known as a frequency spectrum. For instance, the transform of a musical chord made up of pure notes is a mathematical representation of the amplitudes of the individual notes that make...
of
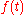 , and
, and  is its complex conjugate
is its complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
.
If the signal is discrete with values
 , over an infinite number of elements, we still have an energy spectral density:
, over an infinite number of elements, we still have an energy spectral density:
where
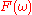 is the discrete-time Fourier transform
is the discrete-time Fourier transformDiscrete-time Fourier transform
In mathematics, the discrete-time Fourier transform is one of the specific forms of Fourier analysis. As such, it transforms one function into another, which is called the frequency domain representation, or simply the "DTFT", of the original function . But the DTFT requires an input function...
of
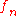 .
.If the number of defined values is finite, the sequence does not have an energy spectral density per se, but the sequence can be treated as periodic, using a Discrete Fourier Transform
Discrete Fourier transform
In mathematics, the discrete Fourier transform is a specific kind of discrete transform, used in Fourier analysis. It transforms one function into another, which is called the frequency domain representation, or simply the DFT, of the original function...
(DFT) to make a discrete spectrum, or it can be extended with zeros and a spectral density can be computed as in the infinite-sequence case.
The continuous and discrete spectral densities are often denoted with the same symbols, as above, though their dimensions and units differ; the continuous case has a time-squared factor that the discrete case does not have. They can be made to have equal dimensions and units by measuring time in units of sample intervals or by scaling the discrete case to the desired time units.
As is always the case, the multiplicative factor of
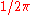 is not absolute, but rather depends on the particular normalizing constants used in the definition of the various Fourier transforms.
is not absolute, but rather depends on the particular normalizing constants used in the definition of the various Fourier transforms.Power spectral density
The above definitions of energy spectral density require that the Fourier transforms of the signals exist, that is, that the signals are integrable/summable or square-integrable/square-summable. (Note: The integral definition of the Fourier transform is only well-defined when the function is integrable. It is not sufficient for a function to be simply square-integrable. In this case one would need to use the Plancherel theoremPlancherel theorem
In mathematics, the Plancherel theorem is a result in harmonic analysis, proved by Michel Plancherel in 1910. It states that the integral of a function's squared modulus is equal to the integral of the squared modulus of its frequency spectrum....
.) An often more useful alternative is the power spectral density (PSD), which describes how the power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
of a signal or time series is distributed with frequency. Here power can be the actual physical power, or more often, for convenience with abstract signals, can be defined as the squared value of the signal, that is, as the actual power dissipated in a purely resistive
Resistor
A linear resistor is a linear, passive two-terminal electrical component that implements electrical resistance as a circuit element.The current through a resistor is in direct proportion to the voltage across the resistor's terminals. Thus, the ratio of the voltage applied across a resistor's...
load if the signal were a voltage
Voltage
Voltage, otherwise known as electrical potential difference or electric tension is the difference in electric potential between two points — or the difference in electric potential energy per unit charge between two points...
applied across it. This instantaneous power (the mean or expected value of which is the average power) is then given by
-
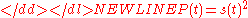
for a signal .
.
Since a signal with nonzero average power is not square integrable, the Fourier transforms do not exist in this case. Fortunately, the Wiener–Khinchin theoremWiener–Khinchin theoremThe Wiener–Khinchin theorem states that the power spectral density of a wide–sense stationary random process is the Fourier transform of the corresponding autocorrelation function.-History:Norbert Wiener first published the result in...
provides a simple alternative. The PSD is the Fourier transform of the autocorrelation function,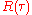 , of the signal if the signal is treated as a wide-sense stationary random processStationary processIn the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
, of the signal if the signal is treated as a wide-sense stationary random processStationary processIn the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
.
These results are expressed in the mathematical formula,
-
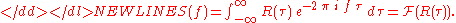
The ensemble average of the average periodogramPeriodogramThe periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898 as in the following quote:...
when the averaging time interval T→∞ can be proved (Brown & Hwang) to approach the Power Spectral Density (PSD):
-

The power of the signal in a given frequency band can be calculated by integrating over positive and negative frequencies,
-
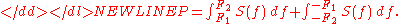
The power spectral density of a signal exists if the signal is a wide-sense stationary processStationary processIn the mathematical sciences, a stationary process is a stochastic process whose joint probability distribution does not change when shifted in time or space...
. If the signal is not wide-sense stationary, then the autocorrelation function must be a function of two variables. In some cases, such as wide-sense cyclostationary processes, a PSD may still exist.
More generally, similar techniques may be used to estimate a time-varying spectral density.
If two signals both possess power spectra (the correct terminology), then a cross-power spectrum can be calculated by using their cross-correlationCross-correlationIn signal processing, cross-correlation is a measure of similarity of two waveforms as a function of a time-lag applied to one of them. This is also known as a sliding dot product or sliding inner-product. It is commonly used for searching a long-duration signal for a shorter, known feature...
function.
Properties of the power spectral density
- spectrum of a real valued process is symmetric:
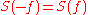
- is continuous and differentiable on [-1/2, +1/2]
- derivative is zero at f = 0
- auto-covariance can be reconstructed by using the Inverse Fourier transform
- describes the distribution of variance across time scales. In particular
-
- is a linear function of the auto-covariance function
- If
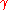 is decomposed into two functions
is decomposed into two functions 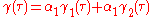 then
then -

- where

- where
- If
The power spectrum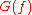 is defined as
is defined as
Cross-spectral density
"Just as the Power Spectral Density (PSD) is the Fourier transform of the auto-covariance function we may define the Cross Spectral Density (CSD) as the Fourier transform of the cross-covariance function."
The PSD is a special case of the cross spectral density (CPSD) function, defined between two signals xn and yn as
-
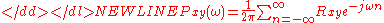
Estimation
The goal of spectral density estimation is to estimateEstimation theoryEstimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
the spectral density of a random signal from a sequence of time samples. Depending on what is known about the signal, estimation techniques can involve parametricParametric statisticsParametric statistics is a branch of statistics that assumes that the data has come from a type of probability distribution and makes inferences about the parameters of the distribution. Most well-known elementary statistical methods are parametric....
or non-parametricNon-parametric statisticsIn statistics, the term non-parametric statistics has at least two different meanings:The first meaning of non-parametric covers techniques that do not rely on data belonging to any particular distribution. These include, among others:...
approaches, and may be based on time-domain or frequency-domain analysis. For example, a common parametric technique involves fitting the observations to an autoregressive modelAutoregressive modelIn statistics and signal processing, an autoregressive model is a type of random process which is often used to model and predict various types of natural phenomena...
. A common non-parametric technique is the periodogramPeriodogramThe periodogram is an estimate of the spectral density of a signal. The term was coined by Arthur Schuster in 1898 as in the following quote:...
.
The spectral density is usually estimated using Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
methods, but other techniques such as Welch's method and the maximum entropyMaximum entropy spectral estimationThe maximum entropy method applied to spectral density estimation. The overall idea is that the maximum entropy rate stochastic process that satisfies the given constant autocorrelation and variance constraints, is a linear Gauss-Markov process with i.i.d...
method can also be used.
Properties
- The spectral density of
 and the autocorrelationAutocorrelationAutocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
and the autocorrelationAutocorrelationAutocorrelation is the cross-correlation of a signal with itself. Informally, it is the similarity between observations as a function of the time separation between them...
of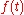 form a Fourier transform pair (for PSD versus ESD, different definitions of autocorrelation function are used).
form a Fourier transform pair (for PSD versus ESD, different definitions of autocorrelation function are used).
- One of the results of Fourier analysis is Parseval's theoremParseval's theoremIn mathematics, Parseval's theorem usually refers to the result that the Fourier transform is unitary; loosely, that the sum of the square of a function is equal to the sum of the square of its transform. It originates from a 1799 theorem about series by Marc-Antoine Parseval, which was later...
which states that the area under the energy spectral density curve is equal to the area under the square of the magnitude of the signal, the total energy:
- The above theorem holds true in the discrete cases as well. A similar result holds for the total power in a power spectral density being equal to the corresponding mean total signal power, which is the autocorrelation function at zero lag.
Related concepts
- Most "frequency" graphs really display only the spectral density. Sometimes the complete frequency spectrum is graphed in 2 parts, "amplitude" versus frequency (which is the spectral density) and "phasePhase (waves)Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
" versus frequency (which contains the rest of the information from the frequency spectrum).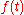 cannot be recovered from the spectral density part alone — the "temporal information" is lost.
cannot be recovered from the spectral density part alone — the "temporal information" is lost.
- The spectral centroidSpectral centroidThe spectral centroid is a measure used in digital signal processing to characterise a spectrum. It indicates where the "center of mass" of the spectrum is...
of a signal is the midpoint of its spectral density function, i.e. the frequency that divides the distribution into two equal parts.
- The spectral edge frequencySpectral edge frequencyThe spectral edge frequency or SEF is a measure used in signal processing. It is usually expressed as "SEF x", which stands for the frequency below which x percent of the total power of a given signal are located...
of a signal is an extension of the previous concept to any proportion instead of two equal parts.
- Spectral density is a function of frequency, not a function of time. However, the spectral density of small "windows" of a longer signal may be calculated, and plotted versus time associated with the window. Such a graph is called a spectrogramSpectrogramA spectrogram is a time-varying spectral representation that shows how the spectral density of a signal varies with time. Also known as spectral waterfalls, sonograms, voiceprints, or voicegrams, spectrograms are used to identify phonetic sounds, to analyse the cries of animals; they were also...
. This is the basis of a number of spectral analysis techniques such as the short-time Fourier transformShort-time Fourier transformThe short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time....
and wavelets.
- In radiometryRadiometryIn optics, radiometry is a set of techniques for measuring electromagnetic radiation, including visible light. Radiometric techniques characterize the distribution of the radiation's power in space, as opposed to photometric techniques, which characterize the light's interaction with the human eye...
and colorimetryColorimetryColorimetry is "the science and technology used to quantify and describe physically the human color perception."It is similar to spectrophotometry, but is distinguished by its interest in reducing spectra to the physical correlates of color perception, most often the CIE 1931 XYZ color space...
(or color science more generally), the spectral power distributionSpectral power distributionIn color science and radiometry, a spectral power distribution describes the power per unit area per unit wavelength of an illumination , or more generally, the per-wavelength contribution to any radiometric quantity .Mathematically, for the spectral...
(SPD) of a light source is a measure of the power carried by each frequency or "color" in a light source. The light spectrum is usually measured at points (often 31) along the visible spectrumVisible spectrumThe visible spectrum is the portion of the electromagnetic spectrum that is visible to the human eye. Electromagnetic radiation in this range of wavelengths is called visible light or simply light. A typical human eye will respond to wavelengths from about 390 to 750 nm. In terms of...
, in wavelength space instead of frequency space, which makes it not strictly a spectral density. Some spectrophotometersSpectrophotometryIn chemistry, spectrophotometry is the quantitative measurement of the reflection or transmission properties of a material as a function of wavelength...
can measure increments as fine as 1 or 2 nanometers. Values are used to calculate other specifications and then plotted to demonstrate the spectral attributes of the source. This can be a helpful tool in analyzing the colorColorColor or colour is the visual perceptual property corresponding in humans to the categories called red, green, blue and others. Color derives from the spectrum of light interacting in the eye with the spectral sensitivities of the light receptors...
characteristics of a particular source.
Electrical engineering
The concept and use of the power spectrum of a signal is fundamental in electrical engineeringElectrical engineeringElectrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, especially in electronic communication systems, including radio communications, radarRadarRadar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
s, and related systems, plus passive [remote sensing] technology. Much effort has been expended and millions of dollars spent on developing and producing electronic instruments called "spectrum analyzerSpectrum analyzerA spectrum analyzer measures the magnitude of an input signal versus frequency within the full frequency range of the instrument. The primary use is to measure the power of the spectrum of known and unknown signals...
s" for aiding electrical engineers and technicians in observing and measuring the power spectra of signals. The cost of a spectrum analyzer varies depending on its frequency range, its bandwidth (signal processing), and its accuracy. The higher the frequency range (S-band, C-band, X-band, Ku-band, K-band, Ka-band, etc.), the more difficult the components are to make, and the more expensive the spectrum analyzer is. Also, the wider the bandwidth that a spectrum analyzer possesses, the more costly that it is, and the capability for more accurate measurements increases costs as well.
The spectrum analyzer measures the magnitude of the short-time Fourier transformShort-time Fourier transformThe short-time Fourier transform , or alternatively short-term Fourier transform, is a Fourier-related transform used to determine the sinusoidal frequency and phase content of local sections of a signal as it changes over time....
(STFT) of an input signal. If the signal being analyzed can be considered a stationary process, the STFT is a good smoothed estimate of its power spectral density.
See also
- Noise spectral densityNoise spectral densityIn communications, noise spectral density No is the noise power per unit of bandwidth; that is, it is the power spectral density of the noise. It has dimension of power/frequency , whose SI coherent unit is watts per hertz, which is equivalent to watt-seconds or joules...
- Spectral density estimationSpectral density estimationIn statistical signal processing, the goal of spectral density estimation is to estimate the spectral density of a random signal from a sequence of time samples of the signal. Intuitively speaking, the spectral density characterizes the frequency content of the signal...
- Spectral efficiencySpectral efficiencySpectral efficiency, spectrum efficiency or bandwidth efficiency refers to the information rate that can be transmitted over a given bandwidth in a specific communication system...
- Colors of noiseColors of noiseWhile noise is by definition derived from a random signal, it can have different characteristic statistical properties corresponding to different mappings from a source of randomness to the concrete noise. Spectral density is such a property, which can be used to distinguish different types of noise...
- Spectral leakageSpectral leakageSpectral leakage is an effect in the frequency analysis of finite-length signals or finite-length segments of infinite signals where it appears as if some energy has "leaked" out of the original signal spectrum into other frequencies....
- Window functionWindow functionIn signal processing, a window function is a mathematical function that is zero-valued outside of some chosen interval. For instance, a function that is constant inside the interval and zero elsewhere is called a rectangular window, which describes the shape of its graphical representation...
- Frequency domainFrequency domainIn electronics, control systems engineering, and statistics, frequency domain is a term used to describe the domain for analysis of mathematical functions or signals with respect to frequency, rather than time....
- Frequency spectrumFrequency spectrumThe frequency spectrum of a time-domain signal is a representation of that signal in the frequency domain. The frequency spectrum can be generated via a Fourier transform of the signal, and the resulting values are usually presented as amplitude and phase, both plotted versus frequency.Any signal...
- BispectrumBispectrumIn mathematics, in the area of statistical analysis, the bispectrum is a statistic used to search for nonlinear interactions. The Fourier transform of the second-order cumulant, i.e., the autocorrelation function, is the traditional power spectrum...
- The spectral density of
- spectrum of a real valued process is symmetric:
-
-
-