Pullback bundle
Encyclopedia
In mathematics
, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundle
s. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′. The fiber of f*E over a point x in B′ is just the fiber of E over f(x). Thus f*E is the disjoint union
of all these fibers equipped with a suitable topology
.

and equip it with the subspace topology
and the projection map π′ : f*E → B′ given by the projection onto the first factor, i.e.,
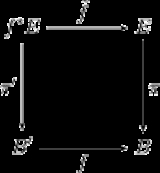
The projection onto the second factor gives a map such that the following diagram commutes
such that the following diagram commutes
:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundle
Fiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
s. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′. The fiber of f*E over a point x in B′ is just the fiber of E over f(x). Thus f*E is the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of all these fibers equipped with a suitable topology
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
.
Formal definition
Let π : E → B be a fiber bundle with abstract fiber F and let f : B′ → B be a continuous map. Define the pullback bundle by
and equip it with the subspace topology
Subspace topology
In topology and related areas of mathematics, a subspace of a topological space X is a subset S of X which is equipped with a natural topology induced from that of X called the subspace topology .- Definition :Given a topological space and a subset S of X, the...
and the projection map π′ : f*E → B′ given by the projection onto the first factor, i.e.,

The projection onto the second factor gives a map
 such that the following diagram commutes
such that the following diagram commutesCommutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:
-

If (U, φ) is a local trivialization of E then (f−1U, ψ) is a local trivialization of f*E where
It then follows that f*E is a fiber bundle over B′ with fiber F. The bundle f*E is called the pullback of E by f or the bundle induced by f. The map is then a bundle morphism covering f.
is then a bundle morphism covering f.
Properties
Any sectionSection (fiber bundle)In the mathematical field of topology, a section of a fiber bundle π is a continuous right inverse of the function π...
s of E over B induces a section of f*E, called the pullback section f*s, simply by defining .
.
If the bundle E → B has structure group G with transition functions tij (with respect to a family of local trivializations {(Ui, φi)} ) then the pullback bundle f*E also has structure group G. The transition functions in f*E are given by
If E → B is a vector bundleVector bundleIn mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
or principal bundlePrincipal bundleIn mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
then so is the pullback f*E. In the case of a principal bundle the right actionGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G on f*E is given by
It then follows that the map is equivariantEquivariantIn mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
is equivariantEquivariantIn mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
and so defines a morphism of principal bundles.
In the language of category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the pullback bundle construction is an example of the more general categorical pullback. As such it satisfies the corresponding universal propertyUniversal propertyIn various branches of mathematics, a useful construction is often viewed as the “most efficient solution” to a certain problem. The definition of a universal property uses the language of category theory to make this notion precise and to study it abstractly.This article gives a general treatment...
.
The construction of the pullback bundle can be carried out in subcategories of the category of topological spaces, such as the category of smooth manifolds. The latter construction is useful in differential geometry and topologyDifferential geometry and topologyDifferential geometry is a mathematical discipline that uses the techniques of differential and integral calculus, as well as linear and multilinear algebra, to study problems in geometry. The theory of plane and space curves and of surfaces in the three-dimensional Euclidean space formed the basis...
Examples: It is illuminating to consider the pullback of the degree 2 map from the circle to itself over the degree 3 or 4 map from the circle to itself. In such examples one sometimes gets a connected and sometimes disconnected space, but always several copies of the circle.
Bundles and sheaves
Bundles may also be described by their sheaves of sectionsSheaf (mathematics)In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
. The pullback of bundles then corresponds to the inverse image of sheavesInverse image functorIn mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
, which is a contravariant functor. A sheaf, however, is more naturally a covariant object, since it has a pushforwardPushforwardThe notion of pushforward in mathematics is "dual" to the notion of pullback, and can mean a number of different, but closely related things.*Pushforward : the differential of a smooth map between manifolds, and the "pushforward" operations it defines.**Pushforward #Pushforward of vector...
, called the direct image of a sheaf. The tension and interplay between bundles and sheaves, or inverse and direct image, can be advantageous in many areas of geometry. However, the direct image of a sheaf of sections of a bundle is not in general the sheaf of sections of some direct image bundle, so that although the notion of a 'pushforward of a bundle' is defined in some contexts (for example, the pushforward by a diffeomorphism), in general it is better understood in the category of sheaves, because the objects it creates cannot in general be bundles.
External links
- Pullback Bundle, PlanetMath

