In set theory

Set theory

Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...

, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality (or size) of infinite sets. They are named after the symbol used to denote them, the Hebrew

Hebrew alphabet

The Hebrew alphabet , known variously by scholars as the Jewish script, square script, block script, or more historically, the Assyrian script, is used in the writing of the Hebrew language, as well as other Jewish languages, most notably Yiddish, Ladino, and Judeo-Arabic. There have been two...

 letter aleph

Aleph

* Aleph or Alef is the first letter of the Semitic abjads descended from Proto-Canaanite, Arabic alphabet, Phoenician alphabet, Hebrew alphabet, Syriac alphabet-People:*Aleph , an Italo disco artist and alias of Dave Rodgers...

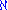 (). This letter was chosen because aleph is the first letter in the hebrew word "אין סוף" (en-sof), that means infinity.

The cardinality of the natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s is (read aleph-naught, aleph-null or aleph-zero), the next larger cardinality is aleph-one 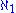, then 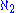and so on. Continuing in this manner, it is possible to define a cardinal number

Cardinal number

In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...

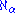  for every ordinal number

Ordinal number

In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...

 α, as described below.

The concept goes back to Georg Cantor

Georg Cantor

Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...

, who defined the notion of cardinality and realized that infinite sets can have different cardinalities.

The aleph numbers differ from the infinity (∞) commonly found in algebra and calculus. Alephs measure the sizes of sets; infinity, on the other hand, is commonly defined as an extreme limit

Limit (mathematics)

In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...

 of the real number line (applied to a function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 or sequence that "diverges

Divergent series

In mathematics, a divergent series is an infinite series that is not convergent, meaning that the infinite sequence of the partial sums of the series does not have a limit....

 to infinity" or "increases without bound"), or an extreme point of the extended real number line

Extended real number line

In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...

.

Aleph-naught

is the cardinality of the set of all natural numbers, and is the first transfinite cardinal

Transfinite number

Transfinite numbers are numbers that are "infinite" in the sense that they are larger than all finite numbers, yet not necessarily absolutely infinite. The term transfinite was coined by Georg Cantor, who wished to avoid some of the implications of the word infinite in connection with these...

. A set has cardinality 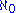if and only if it is countably infinite, which is the case if and only if it can be put into a direct bijection

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

, or "one-to-one correspondence", with the natural numbers. Such sets include the set of all prime number

Prime number

A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...

s, the set of all integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s, the set of all rational number

Rational number

In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...

s, the set of algebraic number

Algebraic number

In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...

s, the set of binary string

String (computer science)

In formal languages, which are used in mathematical logic and theoretical computer science, a string is a finite sequence of symbols that are chosen from a set or alphabet....

s of all finite lengths, and the set of all finite subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

s of any countably infinite set.

If the axiom of countable choice

Axiom of countable choice

The axiom of countable choice or axiom of denumerable choice, denoted ACω, is an axiom of set theory, similar to the axiom of choice. It states that any countable collection of non-empty sets must have a choice function...

 (a weaker version of the axiom of choice) holds, then is smaller than any other infinite cardinal.

Aleph-one

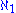is the cardinality of the set of all countable ordinal number

Ordinal number

In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...

s, called ω₁ or (sometimes) Ω. Note that this ω₁ is itself an ordinal number larger than all countable ones, so it is an uncountable set

Uncountable set

In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...

. Therefore 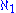is distinct from 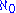. The definition of 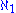implies (in ZF, Zermelo–Fraenkel set theory

Zermelo–Fraenkel set theory

In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...

 without the axiom of choice) that no cardinal number is between 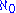and 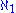. If the axiom of choice (AC) is used, it can be further proved that the class of cardinal numbers is totally ordered, and thus 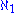is the second-smallest infinite cardinal number. Using AC we can show one of the most useful properties of the set ω₁: any countable subset of ω₁ has an upper bound in ω₁. (This follows from the fact that a countable union of countable sets is countable, one of the most common applications of AC.) This fact is analogous to the situation in 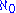: every finite set of natural numbers has a maximum which is also a natural number; that is, finite unions of finite sets are finite.

ω₁ is actually a useful concept, if somewhat exotic-sounding. An example application is "closing" with respect to countable operations; e.g., trying to explicitly describe the σ-algebra

Sigma-algebra

In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...

 generated by an arbitrary collection of subsets. This is harder than most explicit descriptions of "generation" in algebra (vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

s, group

Group theory

In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...

s, etc.) because in those cases we only have to close with respect to finite operations—sums, products, and the like. The process involves defining, for each countable ordinal, via transfinite induction

Transfinite induction

Transfinite induction is an extension of mathematical induction to well-ordered sets, for instance to sets of ordinal numbers or cardinal numbers.- Transfinite induction :Let P be a property defined for all ordinals α...

, a set by "throwing in" all possible countable unions and complements, and taking the union of all that over all of ω₁.

The continuum hypothesis

The cardinality of the set of real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s (cardinality of the continuum

Cardinality of the continuum

In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....

) is 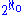. It is not clear where this number fits in the aleph number hierarchy. It follows from ZFC (Zermelo–Fraenkel set theory

Zermelo–Fraenkel set theory

In mathematics, Zermelo–Fraenkel set theory with the axiom of choice, named after mathematicians Ernst Zermelo and Abraham Fraenkel and commonly abbreviated ZFC, is one of several axiomatic systems that were proposed in the early twentieth century to formulate a theory of sets without the paradoxes...

 with the axiom of choice) that the celebrated continuum hypothesis, CH, is equivalent to the identity


CH is independent of ZFC: it can be neither proven nor disproven within the context of that axiom system (provided that ZFC is consistent). That it is consistent with ZFC was demonstrated by Kurt Gödel

Kurt Gödel

Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...

 in 1940 when he showed that its negation is not a theorem of ZFC. That it is independent of ZFC was demonstrated by Paul Cohen

Paul Cohen (mathematician)

Paul Joseph Cohen was an American mathematician best known for his proof of the independence of the continuum hypothesis and the axiom of choice from Zermelo–Fraenkel set theory, the most widely accepted axiomatization of set theory.-Early years:Cohen was born in Long Branch, New Jersey, into a...

 in 1963 when he showed, conversely, that the CH itself is not a theorem of ZFC by the (then novel) method of forcing

Forcing (mathematics)

In the mathematical discipline of set theory, forcing is a technique invented by Paul Cohen for proving consistency and independence results. It was first used, in 1963, to prove the independence of the axiom of choice and the continuum hypothesis from Zermelo–Fraenkel set theory...

.

Aleph-ω

Conventionally the smallest infinite ordinal is denoted ω, and the cardinal number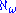 is the least upper bound of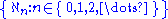
among alephs.

Aleph-ω is the first uncountable cardinal number that can be demonstrated within Zermelo–Fraenkel set theory not to be equal to the cardinality of the set of all real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s; for any positive integer n we can consistently assume that 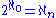, and moreover it is possible to assume 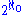is as large as we like. We are only forced to avoid setting it to certain special cardinals with cofinality

Cofinality

In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....

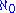 , meaning there is an unbounded function from 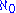to it.

Aleph-α for general α

To define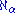 for arbitrary ordinal number , we must define the successor cardinal operation

Successor cardinal

In the theory of cardinal numbers, we can define a successor operation similar to that in the ordinal numbers. This coincides with the ordinal successor operation for finite cardinals, but in the infinite case they diverge because every infinite ordinal and its successor have the same cardinality...

, which assigns to any cardinal number ρ the next larger well-order

Well-order

In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...

ed cardinal ρ. (If the axiom of choice holds, this is the next larger cardinal.)

We can then define the aleph numbers as follows


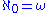
and for λ, an infinite limit ordinal,


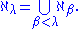
The α-th infinite initial ordinal is written 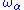. Its cardinality is written 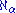. See initial ordinal.

In ZFC the 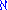function is a bijection between the ordinals and the infinite cardinals.

Fixed points of omega

For any ordinal α we have
In many cases 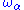is strictly greater than α. For example, for any successor ordinal α this holds. There are, however, some limit ordinals which are fixed point

Fixed point (mathematics)

In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...

s of the omega function, because of the fixed-point lemma for normal functions

Fixed-point lemma for normal functions

The fixed-point lemma for normal functions is a basic result in axiomatic set theory stating that any normal function has arbitrarily large fixed points...

. The first such is the limit of the sequence


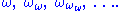
Any weakly inaccessible cardinal

Inaccessible cardinal

In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...

is also a fixed point of the aleph function.