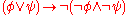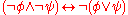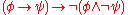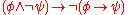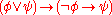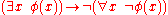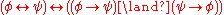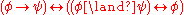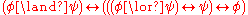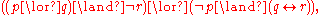Intuitionistic logic
Encyclopedia
Intuitionistic logic, or constructive logic, is a symbolic logic
system differing from classical logic
in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either. In constructive logic, a statement is 'only true' if there is a constructive proof that it is true, and 'only false' if there is a constructive proof that it is false. Operations in constructive logic preserve justification
, rather than truth
.
Syntactically, intuitionist logic is a restriction of classical logic in which the law of excluded middle
and double negation elimination are not axioms of the system, and cannot be proved. There are several semantics commonly employed. One semantics mirrors classical Boolean-valued semantics but uses Heyting algebra
s in place of Boolean algebra
s. Another semantics uses Kripke models.
Constructive logic is practically useful because its restrictions produce proofs that have the existence property, making it also suitable for other forms of mathematical constructivism. Informally, this means that given a constructive proof that an object exists, then that constructive proof can be turned into an algorithm for generating an example of it.
Formalized intuitionistic logic was originally developed by Arend Heyting
to provide a formal basis for Brouwer
's programme of intuitionism
.
 The syntax
The syntax
of formulas of intuitionistic logic is similar to propositional logic or first-order logic
. However, intuitionistic connective
s are not definable in terms of each other in the same way as in classical logic
, hence their choice matters. In intuitionistic propositional logic it is customary to use →, ∧, ∨, ⊥ as the basic connectives, treating ¬A as an abbreviation for . In intuitionistic first-order logic both quantifiers ∃, ∀ are needed.
Many tautologies
of classical logic can no longer be proven within intuitionistic logic. Examples include not only the law of excluded middle
, but also Peirce's law
, and even double negation elimination. In classical logic, both and also are theorems. In intuitionistic logic, only the former is a theorem: double negation can be introduced, but it cannot be eliminated. Rejecting may seem strange to those more familiar with classical logic, but proving this statement in constructive logic would require producing a proof for the truth or falsity of all possible statements, which is impossible for a variety of reasons.
Because many classically valid tautologies are not theorems of intuitionistic logic, but all theorems of intuitionist logic are valid classically, intuitionist logic can be viewed as a weakening of classical logic, albeit one with many useful properties.
discovered that a simple restriction of his system LK (his sequent calculus for classical logic) results in a system which is sound and complete with respect to intuitionistic logic. He called this system LJ. In LK any number of formulas is allowed to appear on the conclusion side of a sequent; in contrast LJ allows at most one formula in this position.
Other derivatives of LK are limited to intuitionstic derivations but still allow multiple conclusions in a sequent. LJ' is one example.
. Compare with the deduction system at Propositional calculus#Alternative calculus.
In propositional logic, the inference rule is modus ponens
and the axioms are
To make this a system of first-order predicate logic, the generalization rules
are added, along with the axioms
If one wishes to include a connective for negation rather than consider it an abbreviation for
for negation rather than consider it an abbreviation for  , it is enough to add:
, it is enough to add:
There are a number of alternatives available if one wishes to omit the connective (false). For example, one may replace the three axioms FALSE, NOT-1', and NOT-2' with the two axioms
(false). For example, one may replace the three axioms FALSE, NOT-1', and NOT-2' with the two axioms
as at Propositional calculus#Axioms. Alternatives to NOT-1 are or
or  .
.
The connective for equivalence may be treated as an abbreviation, with
for equivalence may be treated as an abbreviation, with  standing for
standing for  . Alternatively, one may add the axioms
. Alternatively, one may add the axioms
IFF-1 and IFF-2 can, if desired, be combined into a single axiom using conjunction.
using conjunction.
In general, one may take as the extra axiom any classical tautology that is not valid in the two-element Kripke frame (in other words, that is not included in Smetanich's logic
(in other words, that is not included in Smetanich's logic
).
Another relationship is given by the Gödel–Gentzen negative translation
, which provides an embedding
of classical first-order logic into intuitionistic logic: a first-order formula is provable in classical logic if and only if its Gödel–Gentzen translation is provable intuitionistically. Therefore intuitionistic logic can instead be seen as a means of extending classical logic with constructive semantics.
In 1932, Kurt Gödel
defined a system of Gödel logics intermediate between classical and intuitionistic logic; such logics are known as intermediate logic
s.
in 1932 showed that intuitionistic logic is not a finitely-many valued logic. (See the section titled Heyting algebra semantics below for a sort of "infinitely-many valued logic" interpretation of intuitionistic logic.)
, disjunction
, or implication
as primitive, and define the other two in terms of it together with negation, such as in Łukasiewicz's three axioms of propositional logic. It is even possible to define all four in terms of a sole sufficient operator such as the Peirce arrow (NOR) or Sheffer stroke
(NAND). Similarly, in classical first-order logic, one of the quantifiers can be defined in terms of the other and negation.
These are fundamentally consequences of the law of bivalence, which makes all such connectives merely Boolean functions. The law of bivalence does not hold in intuitionistic logic, only the law of non-contradiction. As a result none of the basic connectives can be dispensed with, and the above axioms are all necessary. Most of the classical identities are only theorems of intuitionistic logic in one direction, although some are theorems in both directions. They are as follows:
Conjunction versus disjunction:
Conjunction versus implication:
Disjunction versus implication:
Universal versus existential quantification:
So, for example, "a or b" is a stronger statement than "if not a, then b", whereas these are classically interchangeable. On the other hand, "not (a or b)" is equivalent to "not a, and also not b".
If we include equivalence in the list of connectives, some of the connectives become definable from others:
In particular, {∨, ↔, ⊥} and {∨, ↔, ¬} are complete bases of intuitionistic connectives.
As shown by Alexander Kuznetsov, either of the following connectives – the first one ternary, the second one quinary – is by itself functionally complete: either one can serve the role of a sole sufficient operator for intuitionistic propositional logic, thus forming an analog of the Sheffer stroke
from classical propositional logic:
s or, equivalently, by Kripke semantics
.
—that is, for any assignment of values to its variables.
A corresponding theorem is true for intuitionistic logic, but instead of assigning each formula a value from a Boolean algebra, one uses values from a Heyting algebra
, of which Boolean algebras are a special case.
A formula is valid in intuitionistic logic if and only if it receives the value of the top element for any valuation on any Heyting algebra.
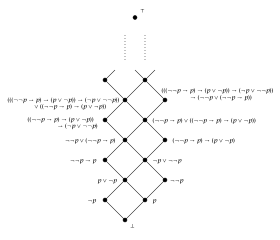
It can be shown that to recognize valid formulas, it is sufficient to consider a single Heyting algebra whose elements are the open subsets of the real line R. In this algebra, the ∧ and ∨ operations correspond to set intersection and union, and the value assigned to a formula A → B is int(AC ∪ B), the interior
of the union of the value of B and the complement
of the value of A. The bottom element is the empty set ∅, and the top element is the entire line R. The negation ¬A of a formula A is (as usual) defined to be A → ∅. The value of ¬A then reduces to int(AC), the interior of the complement of the value of A, also known as the exterior
of A. With these assignments, intuitionistically valid formulas are precisely those that are assigned the value of the entire line.
For example, the formula ¬(A ∧ ¬A) is valid, because no matter what set X is chosen as the value of the formula A, the value of ¬(A ∧ ¬A) can be shown to be the entire line:
A theorem of topology
tells us that int(XC) is a subset of XC, so the intersection is empty, leaving:
So the valuation of this formula is true, and indeed the formula is valid.
But the law of the excluded middle, A ∨ ¬A, can be shown to be invalid by letting the value of A be {y : y > 0 }. Then the value of ¬A is the interior of {y : y ≤ 0 }, which is
{y : y < 0 }, and the value of the formula is the union of
{y : y > 0 }
and
{y : y < 0 }, which is {y : y ≠ 0 }, not the entire line.
The interpretation
of any intuitionistically valid formula in the infinite Heyting algebra described above results in the top element, representing true, as the valuation of the formula, regardless of what values from the algebra are assigned to the variables of the formula. Conversely, for every invalid formula, there is an assignment of values to the variables that yields a valuation that differs from the top element. No finite Heyting algebra has both these properties.
, Saul Kripke
created another semantics for intuitionistic logic, known as Kripke semantics or relational semantics.
to a paraconsistent logic
known as Brazilian, anti-intuitionistic or dual-intuitionistic logic.
The subsystem of intuitionistic logic with the FALSE axiom removed is known as minimal logic
.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
system differing from classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
in its definition of the meaning of a statement being true. In classical logic, all well-formed statements are assumed to be either true or false, even if we do not have a proof of either. In constructive logic, a statement is 'only true' if there is a constructive proof that it is true, and 'only false' if there is a constructive proof that it is false. Operations in constructive logic preserve justification
Theory of justification
Theory of justification is a part of epistemology that attempts to understand the justification of propositions and beliefs. Epistemologists are concerned with various epistemic features of belief, which include the ideas of justification, warrant, rationality, and probability...
, rather than truth
Truth
Truth has a variety of meanings, such as the state of being in accord with fact or reality. It can also mean having fidelity to an original or to a standard or ideal. In a common usage, it also means constancy or sincerity in action or character...
.
Syntactically, intuitionist logic is a restriction of classical logic in which the law of excluded middle
Law of excluded middle
In logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
and double negation elimination are not axioms of the system, and cannot be proved. There are several semantics commonly employed. One semantics mirrors classical Boolean-valued semantics but uses Heyting algebra
Heyting algebra
In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
s in place of Boolean algebra
Boolean algebra
In abstract algebra, a Boolean algebra or Boolean lattice is a complemented distributive lattice. This type of algebraic structure captures essential properties of both set operations and logic operations. A Boolean algebra can be seen as a generalization of a power set algebra or a field of sets...
s. Another semantics uses Kripke models.
Constructive logic is practically useful because its restrictions produce proofs that have the existence property, making it also suitable for other forms of mathematical constructivism. Informally, this means that given a constructive proof that an object exists, then that constructive proof can be turned into an algorithm for generating an example of it.
Formalized intuitionistic logic was originally developed by Arend Heyting
Arend Heyting
Arend Heyting was a Dutch mathematician and logician. He was a student of Luitzen Egbertus Jan Brouwer at the University of Amsterdam, and did much to put intuitionistic logic on a footing where it could become part of mathematical logic...
to provide a formal basis for Brouwer
Luitzen Egbertus Jan Brouwer
Luitzen Egbertus Jan Brouwer FRS , usually cited as L. E. J. Brouwer but known to his friends as Bertus, was a Dutch mathematician and philosopher, a graduate of the University of Amsterdam, who worked in topology, set theory, measure theory and complex analysis.-Biography:Early in his career,...
's programme of intuitionism
Intuitionism
In the philosophy of mathematics, intuitionism, or neointuitionism , is an approach to mathematics as the constructive mental activity of humans. That is, mathematics does not consist of analytic activities wherein deep properties of existence are revealed and applied...
.
Syntax

Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
of formulas of intuitionistic logic is similar to propositional logic or first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. However, intuitionistic connective
Logical connective
In logic, a logical connective is a symbol or word used to connect two or more sentences in a grammatically valid way, such that the compound sentence produced has a truth value dependent on the respective truth values of the original sentences.Each logical connective can be expressed as a...
s are not definable in terms of each other in the same way as in classical logic
Classical logic
Classical logic identifies a class of formal logics that have been most intensively studied and most widely used. The class is sometimes called standard logic as well...
, hence their choice matters. In intuitionistic propositional logic it is customary to use →, ∧, ∨, ⊥ as the basic connectives, treating ¬A as an abbreviation for . In intuitionistic first-order logic both quantifiers ∃, ∀ are needed.
Many tautologies
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
of classical logic can no longer be proven within intuitionistic logic. Examples include not only the law of excluded middle
Law of excluded middle
In logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
, but also Peirce's law
Peirce's law
In logic, Peirce's law is named after the philosopher and logician Charles Sanders Peirce. It was taken as an axiom in his first axiomatisation of propositional logic. It can be thought of as the law of excluded middle written in a form that involves only one sort of connective, namely...
, and even double negation elimination. In classical logic, both and also are theorems. In intuitionistic logic, only the former is a theorem: double negation can be introduced, but it cannot be eliminated. Rejecting may seem strange to those more familiar with classical logic, but proving this statement in constructive logic would require producing a proof for the truth or falsity of all possible statements, which is impossible for a variety of reasons.
Because many classically valid tautologies are not theorems of intuitionistic logic, but all theorems of intuitionist logic are valid classically, intuitionist logic can be viewed as a weakening of classical logic, albeit one with many useful properties.
Sequent calculus
GentzenGerhard Gentzen
Gerhard Karl Erich Gentzen was a German mathematician and logician. He had his major contributions in the foundations of mathematics, proof theory, especially on natural deduction and sequent calculus...
discovered that a simple restriction of his system LK (his sequent calculus for classical logic) results in a system which is sound and complete with respect to intuitionistic logic. He called this system LJ. In LK any number of formulas is allowed to appear on the conclusion side of a sequent; in contrast LJ allows at most one formula in this position.
Other derivatives of LK are limited to intuitionstic derivations but still allow multiple conclusions in a sequent. LJ' is one example.
Hilbert-style calculus
Intuitionistic logic can be defined using the following Hilbert-style calculusHilbert-style deduction system
In logic, especially mathematical logic, a Hilbert system, sometimes called Hilbert calculus or Hilbert–Ackermann system, is a type of system of formal deduction attributed to Gottlob Frege and David Hilbert...
. Compare with the deduction system at Propositional calculus#Alternative calculus.
In propositional logic, the inference rule is modus ponens
Modus ponens
In classical logic, modus ponendo ponens or implication elimination is a valid, simple argument form. It is related to another valid form of argument, modus tollens. Both Modus Ponens and Modus Tollens can be mistakenly used when proving arguments...
- MP: from
 and
and  infer
infer 
and the axioms are
- THEN-1:
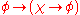
- THEN-2:
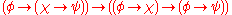
- AND-1:
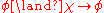
- AND-2:

- AND-3:
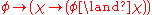
- OR-1:

- OR-2:

- OR-3:
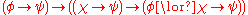
- FALSE:

To make this a system of first-order predicate logic, the generalization rules
Generalization (logic)
In mathematical logic, generalization is an inference rule of predicate calculus. It states that if \vdash P has been derived, then \vdash \forall x \, P can be derived....
-
 -GEN: from
-GEN: from  infer
infer 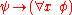 , if
, if  is not free in
is not free in 
-
 -GEN: from
-GEN: from  infer
infer 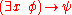 , if
, if  is not free in
is not free in 
are added, along with the axioms
- PRED-1:
 , if the term t is free for substitution for the variable x in
, if the term t is free for substitution for the variable x in  (i.e., if no occurrence of any variable in t becomes bound in
(i.e., if no occurrence of any variable in t becomes bound in 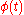 )
) - PRED-2:
 , with the same restriction as for PRED-1
, with the same restriction as for PRED-1
Negation
If one wishes to include a connective
 for negation rather than consider it an abbreviation for
for negation rather than consider it an abbreviation for  , it is enough to add:
, it is enough to add:
- NOT-1':

- NOT-2':
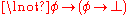
There are a number of alternatives available if one wishes to omit the connective
 (false). For example, one may replace the three axioms FALSE, NOT-1', and NOT-2' with the two axioms
(false). For example, one may replace the three axioms FALSE, NOT-1', and NOT-2' with the two axioms
- NOT-1:

- NOT-2:

as at Propositional calculus#Axioms. Alternatives to NOT-1 are
 or
or  .
.Equivalence
The connective
 for equivalence may be treated as an abbreviation, with
for equivalence may be treated as an abbreviation, with  standing for
standing for  . Alternatively, one may add the axioms
. Alternatively, one may add the axioms- IFF-1:

- IFF-2:

- IFF-3:

IFF-1 and IFF-2 can, if desired, be combined into a single axiom
 using conjunction.
using conjunction.Relation to classical logic
The system of classical logic is obtained by adding any one of the following axioms:-
 (Law of the excluded middle. May also be formulated as
(Law of the excluded middle. May also be formulated as  .)
.) -
 (Double negation elimination)
(Double negation elimination) -
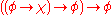 (Peirce's law)
(Peirce's law)
In general, one may take as the extra axiom any classical tautology that is not valid in the two-element Kripke frame
 (in other words, that is not included in Smetanich's logic
(in other words, that is not included in Smetanich's logicIntermediate logic
In mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
).
Another relationship is given by the Gödel–Gentzen negative translation
Gödel–Gentzen negative translation
In proof theory, the Gödel–Gentzen negative translation is a method for embedding classical first-order logic into intuitionistic first-order logic. It is one of a number of double-negation translations that are of importance to the metatheory of intuitionistic logic...
, which provides an embedding
Embedding
In mathematics, an embedding is one instance of some mathematical structure contained within another instance, such as a group that is a subgroup....
of classical first-order logic into intuitionistic logic: a first-order formula is provable in classical logic if and only if its Gödel–Gentzen translation is provable intuitionistically. Therefore intuitionistic logic can instead be seen as a means of extending classical logic with constructive semantics.
In 1932, Kurt Gödel
Kurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
defined a system of Gödel logics intermediate between classical and intuitionistic logic; such logics are known as intermediate logic
Intermediate logic
In mathematical logic, a superintuitionistic logic is a propositional logic extending intuitionistic logic. Classical logic is the strongest consistent superintuitionistic logic, thus consistent superintuitionistic logics are called intermediate logics .-Definition:A superintuitionistic logic is a...
s.
Relation to many-valued logic
Kurt GödelKurt Gödel
Kurt Friedrich Gödel was an Austrian logician, mathematician and philosopher. Later in his life he emigrated to the United States to escape the effects of World War II. One of the most significant logicians of all time, Gödel made an immense impact upon scientific and philosophical thinking in the...
in 1932 showed that intuitionistic logic is not a finitely-many valued logic. (See the section titled Heyting algebra semantics below for a sort of "infinitely-many valued logic" interpretation of intuitionistic logic.)
Non-interdefinability of operators
In classical propositional logic, it is possible to take one of conjunctionLogical conjunction
In logic and mathematics, a two-place logical operator and, also known as logical conjunction, results in true if both of its operands are true, otherwise the value of false....
, disjunction
Logical disjunction
In logic and mathematics, a two-place logical connective or, is a logical disjunction, also known as inclusive disjunction or alternation, that results in true whenever one or more of its operands are true. E.g. in this context, "A or B" is true if A is true, or if B is true, or if both A and B are...
, or implication
Material conditional
The material conditional, also known as material implication, is a binary truth function, such that the compound sentence p→q is logically equivalent to the negative compound: not . A material conditional compound itself is often simply called a conditional...
as primitive, and define the other two in terms of it together with negation, such as in Łukasiewicz's three axioms of propositional logic. It is even possible to define all four in terms of a sole sufficient operator such as the Peirce arrow (NOR) or Sheffer stroke
Sheffer stroke
In Boolean functions and propositional calculus, the Sheffer stroke, named after Henry M. Sheffer, written "|" , "Dpq", or "↑", denotes a logical operation that is equivalent to the negation of the conjunction operation, expressed in ordinary language as "not both"...
(NAND). Similarly, in classical first-order logic, one of the quantifiers can be defined in terms of the other and negation.
These are fundamentally consequences of the law of bivalence, which makes all such connectives merely Boolean functions. The law of bivalence does not hold in intuitionistic logic, only the law of non-contradiction. As a result none of the basic connectives can be dispensed with, and the above axioms are all necessary. Most of the classical identities are only theorems of intuitionistic logic in one direction, although some are theorems in both directions. They are as follows:
Conjunction versus disjunction:
Conjunction versus implication:
Disjunction versus implication:
Universal versus existential quantification:
So, for example, "a or b" is a stronger statement than "if not a, then b", whereas these are classically interchangeable. On the other hand, "not (a or b)" is equivalent to "not a, and also not b".
If we include equivalence in the list of connectives, some of the connectives become definable from others:
In particular, {∨, ↔, ⊥} and {∨, ↔, ¬} are complete bases of intuitionistic connectives.
As shown by Alexander Kuznetsov, either of the following connectives – the first one ternary, the second one quinary – is by itself functionally complete: either one can serve the role of a sole sufficient operator for intuitionistic propositional logic, thus forming an analog of the Sheffer stroke
Sheffer stroke
In Boolean functions and propositional calculus, the Sheffer stroke, named after Henry M. Sheffer, written "|" , "Dpq", or "↑", denotes a logical operation that is equivalent to the negation of the conjunction operation, expressed in ordinary language as "not both"...
from classical propositional logic:
Semantics
The semantics are rather more complicated than for the classical case. A model theory can be given by Heyting algebraHeyting algebra
In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
s or, equivalently, by Kripke semantics
Kripke semantics
Kripke semantics is a formal semantics for non-classical logic systems created in the late 1950s and early 1960s by Saul Kripke. It was first made for modal logics, and later adapted to intuitionistic logic and other non-classical systems...
.
Heyting algebra semantics
In classical logic, we often discuss the truth values that a formula can take. The values are usually chosen as the members of a Boolean algebra. The meet and join operations in the Boolean algebra are identified with the ∧ and ∨ logical connectives, so that the value of a formula of the form A ∧ B is the meet of the value of A and the value of B in the Boolean algebra. Then we have the useful theorem that a formula is a valid sentence of classical logic if and only if its value is 1 for every valuationValuation (logic)
In logic and model theory, a valuation can be:*In propositional logic, an assignment of truth values to propositional variables, with a corresponding assignment of truth values to all propositional formulas with those variables....
—that is, for any assignment of values to its variables.
A corresponding theorem is true for intuitionistic logic, but instead of assigning each formula a value from a Boolean algebra, one uses values from a Heyting algebra
Heyting algebra
In mathematics, a Heyting algebra, named after Arend Heyting, is a bounded lattice equipped with a binary operation a→b of implication such that ∧a ≤ b, and moreover a→b is the greatest such in the sense that if c∧a ≤ b then c ≤ a→b...
, of which Boolean algebras are a special case.
A formula is valid in intuitionistic logic if and only if it receives the value of the top element for any valuation on any Heyting algebra.
It can be shown that to recognize valid formulas, it is sufficient to consider a single Heyting algebra whose elements are the open subsets of the real line R. In this algebra, the ∧ and ∨ operations correspond to set intersection and union, and the value assigned to a formula A → B is int(AC ∪ B), the interior
Interior (topology)
In mathematics, specifically in topology, the interior of a set S of points of a topological space consists of all points of S that do not belong to the boundary of S. A point that is in the interior of S is an interior point of S....
of the union of the value of B and the complement
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
of the value of A. The bottom element is the empty set ∅, and the top element is the entire line R. The negation ¬A of a formula A is (as usual) defined to be A → ∅. The value of ¬A then reduces to int(AC), the interior of the complement of the value of A, also known as the exterior
Exterior (topology)
In topology, the exterior of a subset S of a topological space X is the union of all open sets of X which are disjoint from S. It is itself an open set and is disjoint from S...
of A. With these assignments, intuitionistically valid formulas are precisely those that are assigned the value of the entire line.
For example, the formula ¬(A ∧ ¬A) is valid, because no matter what set X is chosen as the value of the formula A, the value of ¬(A ∧ ¬A) can be shown to be the entire line:
- Value(¬(A ∧ ¬A)) =
- int((Value(A ∧ ¬A))C) =
- int((Value(A) ∩ Value(¬A))C) =
- int((X ∩ int((Value(A))C))C) =
- int((X ∩ int(XC))C)
A theorem of topology
Topology
Topology is a major area of mathematics concerned with properties that are preserved under continuous deformations of objects, such as deformations that involve stretching, but no tearing or gluing...
tells us that int(XC) is a subset of XC, so the intersection is empty, leaving:
- int(∅C) = int(R) = R
So the valuation of this formula is true, and indeed the formula is valid.
But the law of the excluded middle, A ∨ ¬A, can be shown to be invalid by letting the value of A be {y : y > 0 }. Then the value of ¬A is the interior of {y : y ≤ 0 }, which is
{y : y < 0 }, and the value of the formula is the union of
{y : y > 0 }
and
{y : y < 0 }, which is {y : y ≠ 0 }, not the entire line.
The interpretation
Interpretation (logic)
An interpretation is an assignment of meaning to the symbols of a formal language. Many formal languages used in mathematics, logic, and theoretical computer science are defined in solely syntactic terms, and as such do not have any meaning until they are given some interpretation...
of any intuitionistically valid formula in the infinite Heyting algebra described above results in the top element, representing true, as the valuation of the formula, regardless of what values from the algebra are assigned to the variables of the formula. Conversely, for every invalid formula, there is an assignment of values to the variables that yields a valuation that differs from the top element. No finite Heyting algebra has both these properties.
Kripke semantics
Building upon his work on semantics of modal logicModal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
, Saul Kripke
Saul Kripke
Saul Aaron Kripke is an American philosopher and logician. He is a professor emeritus at Princeton and teaches as a Distinguished Professor of Philosophy at the CUNY Graduate Center...
created another semantics for intuitionistic logic, known as Kripke semantics or relational semantics.
Relation to other logics
Intutionistic logic is related by dualityDuality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
to a paraconsistent logic
Paraconsistent logic
A paraconsistent logic is a logical system that attempts to deal with contradictions in a discriminating way. Alternatively, paraconsistent logic is the subfield of logic that is concerned with studying and developing paraconsistent systems of logic.Inconsistency-tolerant logics have been...
known as Brazilian, anti-intuitionistic or dual-intuitionistic logic.
The subsystem of intuitionistic logic with the FALSE axiom removed is known as minimal logic
Minimal logic
Minimal logic, or minimal calculus, is a symbolic logic system originally developed by Ingebrigt Johansson. It is a variant of intuitionistic logic that rejects not only the classical law of excluded middle , but also the principle of explosion .Just like intuitionistic logic, minimal logic can be...
.
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: "Intuitionistic Logic" -- by Joan Moschovakis.