Limit cardinal
Encyclopedia
In mathematics
, limit cardinals are certain cardinal number
s. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal
nor zero. This means that one cannot "reach" λ by repeated successor operations. These cardinals are sometimes called simply "limit cardinals" when the context is clear.
A cardinal λ is a strong limit cardinal if λ cannot be reached by repeated powerset operations. This means that λ is nonzero and, for all κ < λ, 2κ < λ. Every strong limit cardinal is also a weak limit cardinal, because κ+ ≤ 2κ for every cardinal κ.
The first infinite cardinal,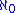
(aleph-naught), is a strong limit cardinal, and hence also a weak limit cardinal.
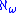is a weak limit cardinal, defined as the union of all the alephs before it; and in general 
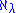for any limit ordinal λ is a weak limit cardinal.
The ב operation
can be used to obtain strong limit cardinals. This operation is a map from ordinals to cardinals defined as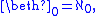
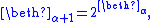(the smallest ordinal equinumerous with the powerset)
The cardinal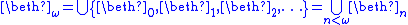
is a strong limit cardinal of cofinality
ω. More generally, given any ordinal α, the cardinal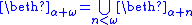
is a strong limit cardinal. Thus there are arbitrarily large strong limit cardinals.
then the cardinal number is of the form 
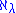for the same ordinal subscript λ. The ordinal λ determines whether 
is a weak limit cardinal. Because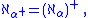 
if λ is a successor ordinal then 
is not a weak limit. Conversely, if a cardinal κ is a successor cardinal, say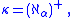 
then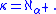 
Thus, in general, 
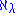is a weak limit cardinal if and only if λ is zero or a limit ordinal.
Although the ordinal subscript tells whether a cardinal is a weak limit, it does not tell whether a cardinal is a strong limit. For example, ZFC proves that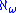
is a weak limit cardinal, but neither proves nor disproves that 
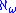is a strong limit cardinal (Hrbacek and Jech 1999:168). The generalized continuum hypothesis states that 
for every infinite cardinal κ. Under this hypothesis, the notions of weak and strong limit cardinals coincide.
. For a weak (resp. strong) limit cardinal κ the requirement that cf(κ) = κ (i.e. κ be regular
) so that κ cannot be expressed as a sum (union) of fewer than κ smaller cardinals. Such a cardinal is called a weakly (resp. strongly) inaccessible cardinal
. The preceding examples both are singular cardinals of cofinality ω and hence they are not inaccessible.
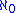would be an inaccessible cardinal of both "strengths" except that the definition of inaccessible requires that they be uncountable. Standard Zermelo-Fraenkel set theory with the Axiom of Choice (ZFC) cannot even prove the existence of an inaccessible cardinal of either kind above 
. These form the first in a hierarchy of large cardinals.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, limit cardinals are certain cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal
Successor cardinal
In the theory of cardinal numbers, we can define a successor operation similar to that in the ordinal numbers. This coincides with the ordinal successor operation for finite cardinals, but in the infinite case they diverge because every infinite ordinal and its successor have the same cardinality...
nor zero. This means that one cannot "reach" λ by repeated successor operations. These cardinals are sometimes called simply "limit cardinals" when the context is clear.
A cardinal λ is a strong limit cardinal if λ cannot be reached by repeated powerset operations. This means that λ is nonzero and, for all κ < λ, 2κ < λ. Every strong limit cardinal is also a weak limit cardinal, because κ+ ≤ 2κ for every cardinal κ.
The first infinite cardinal,
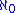(aleph-naught), is a strong limit cardinal, and hence also a weak limit cardinal.Constructions
One way to construct limit cardinals is via the union operation: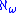 is a weak limit cardinal, defined as the union of all the alephs before it; and in general 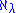for any limit ordinal λ is a weak limit cardinal.The ב operation
Beth number
In mathematics, the infinite cardinal numbers are represented by the Hebrew letter \aleph indexed with a subscript that runs over the ordinal numbers...
can be used to obtain strong limit cardinals. This operation is a map from ordinals to cardinals defined as
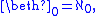
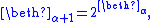(the smallest ordinal equinumerous with the powerset)
- If λ is a limit ordinal,
The cardinal
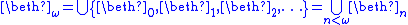
is a strong limit cardinal of cofinality
Cofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
ω. More generally, given any ordinal α, the cardinal
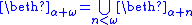
is a strong limit cardinal. Thus there are arbitrarily large strong limit cardinals.
Relationship with ordinal subscripts
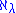If the axiom of choice holds, every cardinal number has an initial ordinal. If that initial ordinal is then the cardinal number is of the form for the same ordinal subscript λ. The ordinal λ determines whether is a weak limit cardinal. Because 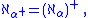if λ is a successor ordinal then is not a weak limit. Conversely, if a cardinal κ is a successor cardinal, say 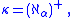then 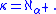Thus, in general, 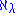is a weak limit cardinal if and only if λ is zero or a limit ordinal.Although the ordinal subscript tells whether a cardinal is a weak limit, it does not tell whether a cardinal is a strong limit. For example, ZFC proves that
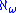is a weak limit cardinal, but neither proves nor disproves that 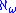is a strong limit cardinal (Hrbacek and Jech 1999:168). The generalized continuum hypothesis states that for every infinite cardinal κ. Under this hypothesis, the notions of weak and strong limit cardinals coincide.The notion of inaccessibility and large cardinals
The preceding defines a notion of "inaccessibility": we are dealing with cases where it is no longer enough to do finitely many iterations of the successor and powerset operations; hence the phrase "cannot be reached" in both of the intuitive definitions above. But the "union operation" always provides another way of "accessing" these cardinals (and indeed, such is the case of limit ordinals as well). Stronger notions of inaccessibility can be defined using cofinalityCofinality
In mathematics, especially in order theory, the cofinality cf of a partially ordered set A is the least of the cardinalities of the cofinal subsets of A....
. For a weak (resp. strong) limit cardinal κ the requirement that cf(κ) = κ (i.e. κ be regular
Regular cardinal
In set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
) so that κ cannot be expressed as a sum (union) of fewer than κ smaller cardinals. Such a cardinal is called a weakly (resp. strongly) inaccessible cardinal
Inaccessible cardinal
In set theory, an uncountable regular cardinal number is called weakly inaccessible if it is a weak limit cardinal, and strongly inaccessible, or just inaccessible, if it is a strong limit cardinal. Some authors do not require weakly and strongly inaccessible cardinals to be uncountable...
. The preceding examples both are singular cardinals of cofinality ω and hence they are not inaccessible.
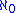would be an inaccessible cardinal of both "strengths" except that the definition of inaccessible requires that they be uncountable. Standard Zermelo-Fraenkel set theory with the Axiom of Choice (ZFC) cannot even prove the existence of an inaccessible cardinal of either kind above . These form the first in a hierarchy of large cardinals.