
Euclidean topology
Encyclopedia
In mathematics, and especially general topology
, the Euclidean topology is an example of a topology given to the set of real number
s, denoted by R. To give the set R a topology means to say which subset
s of R are "open", and to do so in a way that the following axiom
s are met:
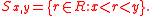
Along with the set R and the empty set ∅, the sets Sx,y with are used as a basis for the Euclidean topology. In other words, the open sets of the Euclidean topology are given by the set R, the empty set ∅ and the unions and finite intersections of various sets Sx,y for different pairs of (x,y).
General topology
In mathematics, general topology or point-set topology is the branch of topology which studies properties of topological spaces and structures defined on them...
, the Euclidean topology is an example of a topology given to the set of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s, denoted by R. To give the set R a topology means to say which subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
s of R are "open", and to do so in a way that the following axiom
Axiom
In traditional logic, an axiom or postulate is a proposition that is not proven or demonstrated but considered either to be self-evident or to define and delimit the realm of analysis. In other words, an axiom is a logical statement that is assumed to be true...
s are met:
- The union of open sets is an open set.
- The finite intersection of open sets is an open set.
- The set R and the empty setEmpty setIn mathematics, and more specifically set theory, the empty set is the unique set having no elements; its size or cardinality is zero. Some axiomatic set theories assure that the empty set exists by including an axiom of empty set; in other theories, its existence can be deduced...
∅ are open sets.
Construction
The set R and the empty set ∅ are required to be open sets, and so we define R and ∅ to be open sets in this topology. Given two real numbers, say x and y, with we define an uncountably infinite family of open sets denoted by Sx,y as follows: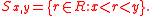
Along with the set R and the empty set ∅, the sets Sx,y with are used as a basis for the Euclidean topology. In other words, the open sets of the Euclidean topology are given by the set R, the empty set ∅ and the unions and finite intersections of various sets Sx,y for different pairs of (x,y).
Properties
- The real line, with this topology, is a T5 space. Given two subsets, say A and B, of R with , where A denotes the closureClosure (topology)In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of A, etc., there exist open sets SA and SB with and such that

