Successor cardinal
Encyclopedia
In the theory of cardinal numbers, we can define a successor operation similar to that in the ordinal number
s. This coincides with the ordinal successor operation for finite cardinals, but in the infinite case they diverge because every infinite ordinal and its successor have the same cardinality (a bijection
can be set up between the two by simply sending the last element of the successor to 0, 0 to 1, etc., and fixing ω and all the elements above; in the style of Hilbert's Hotel Infinity
). Using the von Neumann cardinal assignment
and the axiom of choice (AC), this successor operation is easy to define: for a cardinal number κ we have
,
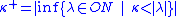where ON is the class of ordinals. That is, the successor cardinal is the cardinality of the least ordinal into which a set of the given cardinality can be mapped one-to-one, but which cannot be mapped one-to-one back into that set.
That the set above is nonempty follows from Hartogs' theorem
, which says that for any well-order
able cardinal, a larger such cardinal is constructible. The minimum actually exists because the ordinals are well-ordered. It is therefore immediate that there is no cardinal number in between κ and κ+. A successor cardinal is a cardinal which is κ+ for some cardinal κ. In the infinite case, the successor operation skips over many ordinal numbers; in fact, every infinite cardinal is a limit ordinal. Therefore, the successor operation on cardinals gains a lot of power in the infinite case (relative the ordinal successorship operation), and consequently the cardinal numbers are a very "sparse" subclass of the ordinals. We define the sequence of alephs
(via the axiom of replacement) via this operation, through all the ordinal numbers as follows:
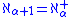
and for λ an infinite limit ordinal,
If β is a successor ordinal
, then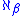
is a successor cardinal. Cardinals which are not successor cardinals are called limit cardinal
s; and by the above definition, if λ is a limit ordinal, then
is a limit cardinal.
The standard definition above is restricted to the case when the cardinal can be well-ordered, i.e. is finite or an aleph. Without the axiom of choice, there are cardinals which cannot be well-ordered. Some mathematicians have defined the successor of such a cardinal as the cardinality of the least ordinal which cannot be mapped one-to-one into a set of the given cardinality. That is:
.
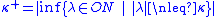Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
s. This coincides with the ordinal successor operation for finite cardinals, but in the infinite case they diverge because every infinite ordinal and its successor have the same cardinality (a bijection
Bijection
A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
can be set up between the two by simply sending the last element of the successor to 0, 0 to 1, etc., and fixing ω and all the elements above; in the style of Hilbert's Hotel Infinity
Hilbert's paradox of the Grand Hotel
Hilbert's paradox of the Grand Hotel is a mathematical veridical paradox about infinite sets presented by German mathematician David Hilbert .-The paradox:...
). Using the von Neumann cardinal assignment
Von Neumann cardinal assignment
The von Neumann cardinal assignment is a cardinal assignment which uses ordinal numbers. For a well-ordered set U, we define its cardinal number to be the smallest ordinal number equinumerous to U. More precisely:...
and the axiom of choice (AC), this successor operation is easy to define: for a cardinal number κ we have
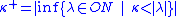,where ON is the class of ordinals. That is, the successor cardinal is the cardinality of the least ordinal into which a set of the given cardinality can be mapped one-to-one, but which cannot be mapped one-to-one back into that set.
That the set above is nonempty follows from Hartogs' theorem
Hartogs number
In mathematics, specifically in axiomatic set theory, a Hartogs number is a particular kind of cardinal number. It was shown by Friedrich Hartogs in 1915, from ZF alone , that there is a least well-ordered cardinal greater than a given well-ordered cardinal.To define the Hartogs number of a set it...
, which says that for any well-order
Well-order
In mathematics, a well-order relation on a set S is a strict total order on S with the property that every non-empty subset of S has a least element in this ordering. Equivalently, a well-ordering is a well-founded strict total order...
able cardinal, a larger such cardinal is constructible. The minimum actually exists because the ordinals are well-ordered. It is therefore immediate that there is no cardinal number in between κ and κ+. A successor cardinal is a cardinal which is κ+ for some cardinal κ. In the infinite case, the successor operation skips over many ordinal numbers; in fact, every infinite cardinal is a limit ordinal. Therefore, the successor operation on cardinals gains a lot of power in the infinite case (relative the ordinal successorship operation), and consequently the cardinal numbers are a very "sparse" subclass of the ordinals. We define the sequence of alephs
Aleph number
In set theory, a discipline within mathematics, the aleph numbers are a sequence of numbers used to represent the cardinality of infinite sets. They are named after the symbol used to denote them, the Hebrew letter aleph...
(via the axiom of replacement) via this operation, through all the ordinal numbers as follows:
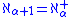
and for λ an infinite limit ordinal,
If β is a successor ordinal
Successor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
, then
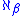is a successor cardinal. Cardinals which are not successor cardinals are called limit cardinalLimit cardinal
In mathematics, limit cardinals are certain cardinal numbers. A cardinal number λ is a weak limit cardinal if λ is neither a successor cardinal nor zero. This means that one cannot "reach" λ by repeated successor operations...
s; and by the above definition, if λ is a limit ordinal, then
is a limit cardinal.The standard definition above is restricted to the case when the cardinal can be well-ordered, i.e. is finite or an aleph. Without the axiom of choice, there are cardinals which cannot be well-ordered. Some mathematicians have defined the successor of such a cardinal as the cardinality of the least ordinal which cannot be mapped one-to-one into a set of the given cardinality. That is:
.
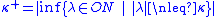