
Cofinality
Encyclopedia
In mathematics
, especially in order theory
, the cofinality cf(A) of a partially ordered set
A is the least of the cardinalities of the cofinal
subsets of A.
This definition of cofinality relies on the axiom of choice, as it uses the fact that every non-empty set of cardinal number
s has a least member. The cofinality of a partially ordered set A can alternatively be defined as the least ordinal
x such that there is a function from x to A with cofinal image
. This second definition makes sense without the axiom of choice. If the axiom of choice is assumed, as will be the case in the rest of this article, then the two definitions are equivalent.
Cofinality can be similarly defined for a directed set
and is used to generalize the notion of a subsequence
in a net
.
cofinal subset, then we can find a subset B which is well-ordered and cofinal in A. Any subset of B is also well-ordered. If two cofinal subsets of B have minimal cardinality (i.e. their cardinality is the cofinality of B), then they are order isomorphic to each other.
 is the smallest ordinal
is the smallest ordinal 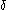 which is the order type
which is the order type
of a cofinal subset of . The cofinality of a set of ordinals or any other well-ordered set is the cofinality of the order type of that set.
. The cofinality of a set of ordinals or any other well-ordered set is the cofinality of the order type of that set.
Thus for a limit ordinal, there exists a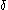 -indexed strictly increasing sequence with limit
-indexed strictly increasing sequence with limit  . For example, the cofinality of ω² is ω, because the sequence ω·m (where m ranges over the natural numbers) tends to ω²; but, more generally, any countable limit ordinal has cofinality ω. An uncountable limit ordinal may have either cofinality ω as does
. For example, the cofinality of ω² is ω, because the sequence ω·m (where m ranges over the natural numbers) tends to ω²; but, more generally, any countable limit ordinal has cofinality ω. An uncountable limit ordinal may have either cofinality ω as does 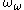 or an uncountable cofinality.
or an uncountable cofinality.
The cofinality of 0 is 0. The cofinality of any successor ordinal
is 1. The cofinality of any limit ordinal is at least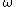 .
.
Every regular ordinal is the initial ordinal of a cardinal. Any limit of regular ordinals is a limit of initial ordinals and thus is also initial but need not be regular. Assuming the Axiom of choice,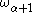 is regular for each α. In this case, the ordinals 0, 1,
is regular for each α. In this case, the ordinals 0, 1, 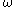 ,
, 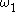 , and
, and  are regular, whereas 2, 3,
are regular, whereas 2, 3,  , and ωω·2 are initial ordinals which are not regular.
, and ωω·2 are initial ordinals which are not regular.
The cofinality of any ordinal α is a regular ordinal, i.e. the cofinality of the cofinality of α is the same as the cofinality of α. So the cofinality operation is idempotent.
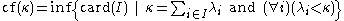
That the set above is nonempty comes from the fact that

i.e. the disjoint union
of κ singleton sets. This implies immediately that cf(κ) ≤ κ.
The cofinality of any totally ordered set is regular, so one has cf(κ) = cf(cf(κ)).
Using König's theorem
, one can prove κ < κcf(κ) and κ < cf(2κ) for any infinite cardinal κ.
The last inequality implies that the cofinality of the cardinality of the continuum must be uncountable. On the other hand,
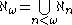 .
.
the ordinal number ω being the first infinite ordinal, so that the cofinality of is card(ω) =
is card(ω) = 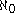 . (In particular,
. (In particular, 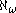 is singular.) Therefore,
is singular.) Therefore,
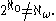
(Compare to the continuum hypothesis
, which states .)
.)
Generalizing this argument, one can prove that for a limit ordinal δ
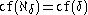 .
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, especially in order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
, the cofinality cf(A) of a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
A is the least of the cardinalities of the cofinal
Cofinal (mathematics)
In mathematics, let A be a set and let ≤ be a binary relation on A. Then a subset B of A is said to be cofinal if it satisfies the following condition:This definition is most commonly applied when A is a partially ordered set or directed set under the relation ≤. Also, the notion of cofinal...
subsets of A.
This definition of cofinality relies on the axiom of choice, as it uses the fact that every non-empty set of cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s has a least member. The cofinality of a partially ordered set A can alternatively be defined as the least ordinal
Ordinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
x such that there is a function from x to A with cofinal image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
. This second definition makes sense without the axiom of choice. If the axiom of choice is assumed, as will be the case in the rest of this article, then the two definitions are equivalent.
Cofinality can be similarly defined for a directed set
Directed set
In mathematics, a directed set is a nonempty set A together with a reflexive and transitive binary relation ≤ , with the additional property that every pair of elements has an upper bound: In other words, for any a and b in A there must exist a c in A with a ≤ c and b ≤...
and is used to generalize the notion of a subsequence
Subsequence
In mathematics, a subsequence is a sequence that can be derived from another sequence by deleting some elements without changing the order of the remaining elements...
in a net
Net (mathematics)
In mathematics, more specifically in general topology and related branches, a net or Moore–Smith sequence is a generalization of the notion of a sequence. In essence, a sequence is a function with domain the natural numbers, and in the context of topology, the range of this function is...
.
Examples
- The cofinality of a partially ordered set with greatest elementGreatest elementIn mathematics, especially in order theory, the greatest element of a subset S of a partially ordered set is an element of S which is greater than or equal to any other element of S. The term least element is defined dually...
is 1 as the set consisting only of the greatest element is cofinal (and must be contained in every other cofinal subset).- In particular, the cofinality of any nonzero finite ordinal, or indeed any finite directed set, is 1, since such sets have a greatest element.
- Every cofinal subset of a partially ordered set must contain all maximal elementMaximal elementIn mathematics, especially in order theory, a maximal element of a subset S of some partially ordered set is an element of S that is not smaller than any other element in S. The term minimal element is defined dually...
s of that set. Thus the cofinality of a finite partially ordered set is equal to the number of its maximal elements.- In particular, let A be a set of size n, and consider the set of subsets of A containing no more than m elements. This is partially ordered under inclusion and the subsets with m elements are maximal. Thus the cofinality of this poset is n chooseBinomial coefficientIn mathematics, binomial coefficients are a family of positive integers that occur as coefficients in the binomial theorem. They are indexed by two nonnegative integers; the binomial coefficient indexed by n and k is usually written \tbinom nk , and it is the coefficient of the x k term in...
m.
- In particular, let A be a set of size n, and consider the set of subsets of A containing no more than m elements. This is partially ordered under inclusion and the subsets with m elements are maximal. Thus the cofinality of this poset is n choose
- A subset of the natural numbers N is cofinal in N if and only if it is infinite, and therefore the cofinality of
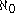 is
is  . Thus
. Thus 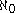 is a regular cardinalRegular cardinalIn set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
is a regular cardinalRegular cardinalIn set theory, a regular cardinal is a cardinal number that is equal to its own cofinality. So, crudely speaking, a regular cardinal is one which cannot be broken into a smaller collection of smaller parts....
. - The cofinality of the real numberReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s with their usual ordering is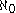 , since N is cofinal in R. The usual ordering of R is not order isomorphic to c, the cardinality of the real numbersCardinality of the continuumIn set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
, since N is cofinal in R. The usual ordering of R is not order isomorphic to c, the cardinality of the real numbersCardinality of the continuumIn set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
, which has cofinality strictly greater than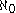 . This demonstrates that the cofinality depends on the order; different orders on the same set may have different cofinality.
. This demonstrates that the cofinality depends on the order; different orders on the same set may have different cofinality.
Properties
If A admits a totally orderedTotal order
In set theory, a total order, linear order, simple order, or ordering is a binary relation on some set X. The relation is transitive, antisymmetric, and total...
cofinal subset, then we can find a subset B which is well-ordered and cofinal in A. Any subset of B is also well-ordered. If two cofinal subsets of B have minimal cardinality (i.e. their cardinality is the cofinality of B), then they are order isomorphic to each other.
Cofinality of ordinals and other well-ordered sets
The cofinality of an ordinal is the smallest ordinal
is the smallest ordinal 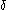 which is the order type
which is the order typeOrder type
In mathematics, especially in set theory, two ordered sets X,Y are said to have the same order type just when they are order isomorphic, that is, when there exists a bijection f: X → Y such that both f and its inverse are monotone...
of a cofinal subset of
 . The cofinality of a set of ordinals or any other well-ordered set is the cofinality of the order type of that set.
. The cofinality of a set of ordinals or any other well-ordered set is the cofinality of the order type of that set.Thus for a limit ordinal, there exists a
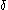 -indexed strictly increasing sequence with limit
-indexed strictly increasing sequence with limit  . For example, the cofinality of ω² is ω, because the sequence ω·m (where m ranges over the natural numbers) tends to ω²; but, more generally, any countable limit ordinal has cofinality ω. An uncountable limit ordinal may have either cofinality ω as does
. For example, the cofinality of ω² is ω, because the sequence ω·m (where m ranges over the natural numbers) tends to ω²; but, more generally, any countable limit ordinal has cofinality ω. An uncountable limit ordinal may have either cofinality ω as does 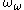 or an uncountable cofinality.
or an uncountable cofinality.The cofinality of 0 is 0. The cofinality of any successor ordinal
Successor ordinal
In set theory, the successor of an ordinal number α is the smallest ordinal number greater than α. An ordinal number that is a successor is called a successor ordinal...
is 1. The cofinality of any limit ordinal is at least
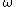 .
.Regular and singular ordinals
A regular ordinal is an ordinal which is equal to its cofinality. A singular ordinal is any ordinal which is not regular.Every regular ordinal is the initial ordinal of a cardinal. Any limit of regular ordinals is a limit of initial ordinals and thus is also initial but need not be regular. Assuming the Axiom of choice,
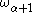 is regular for each α. In this case, the ordinals 0, 1,
is regular for each α. In this case, the ordinals 0, 1, 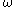 ,
, 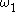 , and
, and  are regular, whereas 2, 3,
are regular, whereas 2, 3,  , and ωω·2 are initial ordinals which are not regular.
, and ωω·2 are initial ordinals which are not regular.The cofinality of any ordinal α is a regular ordinal, i.e. the cofinality of the cofinality of α is the same as the cofinality of α. So the cofinality operation is idempotent.
Cofinality of cardinals
If κ is an infinite cardinal number, then cf(κ) is the least cardinal such that there is an unbounded function from it to κ; and cf(κ) = the cardinality of the smallest collection of sets of strictly smaller cardinals such that their sum is κ; more precisely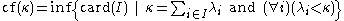
That the set above is nonempty comes from the fact that

i.e. the disjoint union
Disjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of κ singleton sets. This implies immediately that cf(κ) ≤ κ.
The cofinality of any totally ordered set is regular, so one has cf(κ) = cf(cf(κ)).
Using König's theorem
König's theorem (set theory)
In set theory, König's theorem colloquially states that if the axiom of choice holds, I is a set, mi and ni are cardinal numbers for every i in I, and m_i In set theory, König's theorem In set theory, König's theorem (named after the Hungarian mathematician Gyula Kőnig, who published under the...
, one can prove κ < κcf(κ) and κ < cf(2κ) for any infinite cardinal κ.
The last inequality implies that the cofinality of the cardinality of the continuum must be uncountable. On the other hand,
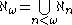 .
.the ordinal number ω being the first infinite ordinal, so that the cofinality of
 is card(ω) =
is card(ω) = 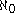 . (In particular,
. (In particular, 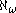 is singular.) Therefore,
is singular.) Therefore,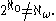
(Compare to the continuum hypothesis
Continuum hypothesis
In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...
, which states
 .)
.)Generalizing this argument, one can prove that for a limit ordinal δ
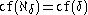 .
.

