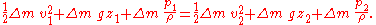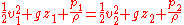
Bernoulli's principle - AbsoluteAstronomy.com

Fluid dynamics

In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...

, Bernoulli's principle states that for an inviscid flow

Inviscid flow

In fluid dynamics there are problems that are easily solved by using the simplifying assumption of an ideal fluid that has no viscosity. The flow of a fluid that is assumed to have no viscosity is called inviscid flow....

, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure

Pressure

Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...

or a decrease in the fluid

Fluid

In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....

's potential energy

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

. Bernoulli's principle is named after the Dutch

Netherlands

The Netherlands is a constituent country of the Kingdom of the Netherlands, located mainly in North-West Europe and with several islands in the Caribbean. Mainland Netherlands borders the North Sea to the north and west, Belgium to the south, and Germany to the east, and shares maritime borders...

-Swiss

Switzerland

Switzerland name of one of the Swiss cantons. ; ; ; or ), in its full name the Swiss Confederation , is a federal republic consisting of 26 cantons, with Bern as the seat of the federal authorities. The country is situated in Western Europe,Or Central Europe depending on the definition....

mathematician

Mathematician

A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....

Daniel Bernoulli

Daniel Bernoulli was a Dutch-Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics...

who published his principle in his book Hydrodynamica in 1738.

Bernoulli's principle can be applied to various types of fluid flow, resulting in what is loosely denoted as Bernoulli's equation. In fact, there are different forms of the Bernoulli equation for different types of flow. The simple form of Bernoulli's principle is valid for incompressible flow

Incompressible flow

In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...

s (e.g. most liquid

Liquid

Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...

flows) and also for compressible flow

Compressible flow

Compressible flow is the area of fluid mechanics that deals with fluids in which the fluid density varies significantly in response to a change in pressure. Compressibility effects are typically considered significant if the Mach number of the flow exceeds 0.3, or if the fluid undergoes very large...

s (e.g. gas

Gas

Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...

es) moving at low Mach number

Mach number

Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...

s. More advanced forms may in some cases be applied to compressible flows at higher Mach number

Mach number

s (see the derivations of the Bernoulli equation).

Bernoulli's principle can be derived from the principle of conservation of energy

Conservation of energy

The nineteenth century law of conservation of energy is a law of physics. It states that the total amount of energy in an isolated system remains constant over time. The total energy is said to be conserved over time...

. This states that, in a steady flow, the sum of all forms of mechanical energy in a fluid along a streamline is the same at all points on that streamline. This requires that the sum of kinetic energy and potential energy remain constant. Thus an increase in the speed of the fluid occurs proportionately with an increase in both its dynamic pressure and kinetic energy

Kinetic energy

The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...

, and a decrease in its static pressure

Static pressure

In fluid mechanics the term static pressure has several uses:* In the design and operation of aircraft, static pressure is the air pressure in the aircraft’s static pressure system....

and potential energy

Potential energy

In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...

. If the fluid is flowing out of a reservoir the sum of all forms of energy is the same on all streamlines because in a reservoir the energy per unit volume (the sum of pressure and gravitational potential ρ g h) is the same everywhere.

Bernoulli's principle can also be derived directly from Newton's 2nd law. If a small volume of fluid is flowing horizontally from a region of high pressure to a region of low pressure, then there is more pressure behind than in front. This gives a net force on the volume, accelerating it along the streamline.

Fluid particles are subject only to pressure and their own weight. If a fluid is flowing horizontally and along a section of a streamline, where the speed increases it can only be because the fluid on that section has moved from a region of higher pressure to a region of lower pressure; and if its speed decreases, it can only be because it has moved from a region of lower pressure to a region of higher pressure. Consequently, within a fluid flowing horizontally, the highest speed occurs where the pressure is lowest, and the lowest speed occurs where the pressure is highest.

Incompressible flow equation

In most flows of liquids, and of gases at low Mach number

Mach number

, the mass density of a fluid parcel can be considered to be constant, regardless of pressure variations in the flow. For this reason the fluid in such flows can be considered to be incompressible and these flows can be described as incompressible flow. Bernoulli performed his experiments on liquids and his equation in its original form is valid only for incompressible flow.
A common form of Bernoulli's equation, valid at any arbitrary

Arbitrary

Arbitrariness is a term given to choices and actions subject to individual will, judgment or preference, based solely upon an individual's opinion or discretion.Arbitrary decisions are not necessarily the same as random decisions...

point along a streamline where gravity is constant, is:
where:

is the fluid flow speed

Speed

In kinematics, the speed of an object is the magnitude of its velocity ; it is thus a scalar quantity. The average speed of an object in an interval of time is the distance traveled by the object divided by the duration of the interval; the instantaneous speed is the limit of the average speed as...

at a point on a streamline,

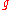is the acceleration due to gravity

Earth's gravity

The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...

is the elevation

Elevation

The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface ....

of the point above a reference plane, with the positive z-direction pointing upward – so in the direction opposite to the gravitational acceleration,

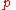is the pressure

Pressure

at the chosen point, and

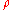is the density

Density

The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...

of the fluid at all points in the fluid.

For conservative force

Conservative force

A conservative force is a force with the property that the work done in moving a particle between two points is independent of the path taken. Equivalently, if a particle travels in a closed loop, the net work done by a conservative force is zero.It is possible to define a numerical value of...

fields, Bernoulli's equation can be generalized as:

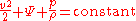
where Ψ is the force potential

Conservative force

at the point considered on the streamline. E.g. for the Earth's gravity Ψ = gz.

The following two assumptions must be met for this Bernoulli equation to apply:

the flow must be incompressible – even though pressure varies, the density must remain constant along a streamline;
friction by viscous forces has to be negligible.

By multiplying with the fluid density

, equation can be rewritten as: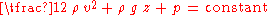

or:

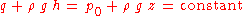
where:

is dynamic pressure,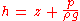

is the piezometric head or hydraulic head

Hydraulic head

Hydraulic head or piezometric head is a specific measurement of water pressure above a geodetic datum. It is usually measured as a water surface elevation, expressed in units of length, at the entrance of a piezometer...

(the sum of the elevation z and the pressure head

Pressure head

Pressure head is a term used in fluid mechanics to represent the internal energy of a fluid due to the pressure exerted on its container. It may also be called static pressure head or simply static head...

) and

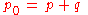is the total pressure

Total pressure

In physics, the term total pressure may indicate two different quantities, both having the dimensions of a pressure:* In fluid dynamics, total pressure refers to the sum of static pressure p, dynamic pressure q, and gravitational head, as expressed by Bernoulli's principle:p_0 = p + q + \rho g...

(the sum of the static pressure p and dynamic pressure q).

The constant in the Bernoulli equation can be normalised. A common approach is in terms of total head or energy head H:

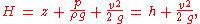
The above equations suggest there is a flow speed at which pressure is zero, and at even higher speeds the pressure is negative. Most often, gases and liquids are not capable of negative absolute pressure, or even zero pressure, so clearly Bernoulli's equation ceases to be valid before zero pressure is reached. In liquids – when the pressure becomes too low – cavitation

Cavitation

Cavitation is the formation and then immediate implosion of cavities in a liquidi.e. small liquid-free zones that are the consequence of forces acting upon the liquid...

occurs. The above equations use a linear relationship between flow speed squared and pressure. At higher flow speeds in gases, or for sound

Sound

Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...

waves in liquid, the changes in mass density become significant so that the assumption of constant density is invalid.

Simplified form

In many applications of Bernoulli's equation, the change in the ρ g z term along the streamline is so small compared with the other terms it can be ignored. For example, in the case of aircraft in flight, the change in height z along a streamline is so small the ρ g z term can be omitted. This allows the above equation to be presented in the following simplified form: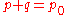

where p₀ is called total pressure, and q is dynamic pressure. Many authors refer to the pressure

Pressure

p as static pressure

Static pressure

In fluid mechanics the term static pressure has several uses:* In the design and operation of aircraft, static pressure is the air pressure in the aircraft’s static pressure system....

to distinguish it from total pressure p₀ and dynamic pressure q. In Aerodynamics, L.J. Clancy writes: "To distinguish it from the total and dynamic pressures, the actual pressure of the fluid, which is associated not with its motion but with its state, is often referred to as the static pressure, but where the term pressure alone is used it refers to this static pressure."

The simplified form of Bernoulli's equation can be summarized in the following memorable word equation:

static pressure + dynamic pressure = total pressure

Every point in a steadily flowing fluid, regardless of the fluid speed at that point, has its own unique static pressure p and dynamic pressure q. Their sum p + q is defined to be the total pressure p₀. The significance of Bernoulli's principle can now be summarized as total pressure is constant along a streamline.

If the fluid flow is irrotational, the total pressure on every streamline is the same and Bernoulli's principle can be summarized as total pressure is constant everywhere in the fluid flow. It is reasonable to assume that irrotational flow exists in any situation where a large body of fluid is flowing past a solid body. Examples are aircraft in flight, and ships moving in open bodies of water. However, it is important to remember that Bernoulli's principle does not apply in the boundary layer

Boundary layer

In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...

or in fluid flow through long pipes

Pipe flow

Pipe flow, a branch of Hydraulics and Fluid Mechanics, is a type of liquid flow within a closed conduit . The other type of flow within a conduit being open channel flow....

.

If the fluid flow at some point along a stream line is brought to rest, this point is called a stagnation point, and at this point the total pressure is equal to the stagnation pressure

Stagnation pressure

In fluid dynamics, stagnation pressure is the static pressure at a stagnation point in a fluid flow.At a stagnation point the fluid velocity is zero and all kinetic energy has been converted into pressure energy . Stagnation pressure is equal to the sum of the free-stream dynamic pressure and...

Applicability of incompressible flow equation to flow of gases

Bernoulli's equation is sometimes valid for the flow of gases: provided that there is no transfer of kinetic or potential energy from the gas flow to the compression or expansion of the gas. If both the gas pressure and volume change simultaneously, then work will be done on or by the gas. In this case, Bernoulli's equation – in its incompressible flow form – can not be assumed to be valid. However if the gas process is entirely isobaric

Isobaric process

An isobaric process is a thermodynamic process in which the pressure stays constant. The term derives from the Greek isos, , and barus,...

, or isochoric

Isochoric process

An isochoric process, also called a constant-volume process, an isovolumetric process, or an isometric process, is a thermodynamic process during which the volume of the closed system undergoing such a process remains constant...

, then no work is done on or by the gas, (so the simple energy balance is not upset). According to the gas law, an isobaric or isochoric process is ordinarily the only way to ensure constant density in a gas. Also the gas density will be proportional to the ratio of pressure and absolute temperature

Temperature

Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...

, however this ratio will vary upon compression or expansion, no matter what non-zero quantity of heat is added or removed. The only exception is if the net heat transfer is zero, as in a complete thermodynamic cycle, or in an individual isentropic (friction

Friction

Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...

less adiabatic) process, and even then this reversible process must be reversed, to restore the gas to the original pressure and specific volume, and thus density. Only then is the original, unmodified Bernoulli equation applicable. In this case the equation can be used if the flow speed of the gas is sufficiently below the speed of sound

Speed of sound

The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....

, such that the variation in density of the gas (due to this effect) along each streamline

Streamlines, streaklines and pathlines

Fluid flow is characterized by a velocity vector field in three-dimensional space, within the framework of continuum mechanics. Streamlines, streaklines and pathlines are field lines resulting from this vector field description of the flow...

can be ignored. Adiabatic flow at less than Mach 0.3 is generally considered to be slow enough.

Unsteady potential flow

The Bernoulli equation for unsteady potential flow is used in the theory of ocean surface wave

Ocean surface wave

In fluid dynamics, wind waves or, more precisely, wind-generated waves are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They usually result from the wind blowing over a vast enough stretch of fluid surface. Waves in the...

s and acoustics

Acoustics

Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...

.

For an irrotational flow, the flow velocity

Flow velocity

In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...

can be described as the gradient

Gradient

In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....

∇φ of a velocity potential φ. In that case, and for a constant density

Density

ρ, the momentum

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

equations of the Euler equations can be integrated to:

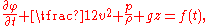
which is a Bernoulli equation valid also for unsteady – or time dependent – flows. Here ∂φ/∂t denotes the partial derivative

Partial derivative

In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...

of the velocity potential φ with respect to time t, and v = |∇φ| is the flow speed.
The function f(t) depends only on time and not on position in the fluid. As a result, the Bernoulli equation at some moment t does not only apply along a certain streamline, but in the whole fluid domain. This is also true for the special case of a steady irrotational flow, in which case f is a constant.

Further f(t) can be made equal to zero by incorporating it into the velocity potential using the transformation

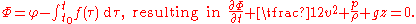
Note that the relation of the potential to the flow velocity is unaffected by this transformation: ∇Φ = ∇φ.

The Bernoulli equation for unsteady potential flow also appears to play a central role in Luke's variational principle

Luke's variational principle

In fluid dynamics, Luke's variational principle is a Lagrangian variational description of the motion of surface waves on a fluid with a free surface, under the action of gravity. This principle is named after J.C. Luke, who published it in 1967...

, a variational description of free-surface flows using the Lagrangian

Lagrangian

The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...

(not to be confused with Lagrangian coordinates).

Compressible flow equation

Bernoulli developed his principle from his observations on liquids, and his equation is applicable only to incompressible fluids, and compressible fluids at very low speeds (perhaps up to 1/3 of the sound speed in the fluid). It is possible to use the fundamental principles of physics to develop similar equations applicable to compressible fluids. There are numerous equations, each tailored for a particular application, but all are analogous to Bernoulli's equation and all rely on nothing more than the fundamental principles of physics such as Newton's laws of motion or the first law of thermodynamics

First law of thermodynamics

The first law of thermodynamics is an expression of the principle of conservation of work.The law states that energy can be transformed, i.e. changed from one form to another, but cannot be created nor destroyed...

Compressible flow in fluid dynamics

For a compressible fluid, with a barotropic

Barotropic

In meteorology, a barotropic atmosphere is one in which the pressure depends only on the density and vice versa, so that isobaric surfaces are also isopycnic surfaces . The isobaric surfaces will also be isothermal surfaces, hence the geostrophic wind is independent of height...

equation of state

Equation of state

In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions...

, and under the action of conservative force

Conservative force

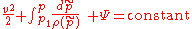(constant along a streamline)

where:

p is the pressure

Pressure

ρ is the density

Density

v is the flow speed

Ψ is the potential associated with the conservative force field, often the gravitational potential

In engineering situations, elevations are generally small compared to the size of the Earth, and the time scales of fluid flow are small enough to consider the equation of state as adiabatic. In this case, the above equation becomes

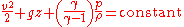(constant along a streamline)

where, in addition to the terms listed above:

γ is the ratio of the specific heats

Heat capacity ratio

The heat capacity ratio or adiabatic index or ratio of specific heats, is the ratio of the heat capacity at constant pressure to heat capacity at constant volume . It is sometimes also known as the isentropic expansion factor and is denoted by \gamma or \kappa . The latter symbol kappa is...

of the fluid

g is the acceleration due to gravity

z is the elevation of the point above a reference plane

In many applications of compressible flow, changes in elevation are negligible compared to the other terms, so the term gz can be omitted. A very useful form of the equation is then:

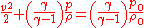
where:

p₀ is the total pressure

Stagnation pressure

ρ₀ is the total density

Compressible flow in thermodynamics

Another useful form of the equation, suitable for use in thermodynamics, is: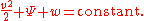

Here w is the enthalpy

Enthalpy

Enthalpy is a measure of the total energy of a thermodynamic system. It includes the internal energy, which is the energy required to create a system, and the amount of energy required to make room for it by displacing its environment and establishing its volume and pressure.Enthalpy is a...

per unit mass, which is also often written as h (not to be confused with "head" or "height").

Note that

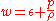where ε is the thermodynamic

Thermodynamics

Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...

energy per unit mass, also known as the specific

Specific energy

Specific energy is defined as the energy per unit mass. Common metric units are J/kg. It is an intensive property. Contrast this with energy, which is an extensive property. There are two main types of specific energy: potential energy and specific kinetic energy. Others are the gray and sievert,...

internal energy

Internal energy

In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...

.

The constant on the right hand side is often called the Bernoulli constant and denoted b. For steady inviscid adiabatic

Adiabatic process

In thermodynamics, an adiabatic process or an isocaloric process is a thermodynamic process in which the net heat transfer to or from the working fluid is zero. Such a process can occur if the container of the system has thermally-insulated walls or the process happens in an extremely short time,...

flow with no additional sources or sinks of energy, b is constant along any given streamline. More generally, when b may vary along streamlines, it still proves a useful parameter, related to the "head" of the fluid (see below).

When the change in Ψ can be ignored, a very useful form of this equation is:

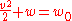
where w₀ is total enthalpy. For a calorically perfect gas such as an ideal gas, the enthalpy is directly proportional to the temperature, and this leads to the concept of the total (or stagnation) temperature.

When shock wave

Shock wave

A shock wave is a type of propagating disturbance. Like an ordinary wave, it carries energy and can propagate through a medium or in some cases in the absence of a material medium, through a field such as the electromagnetic field...

s are present, in a reference frame

Frame of reference

A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...

in which the shock is stationary and the flow is steady, many of the parameters in the Bernoulli equation suffer abrupt changes in passing through the shock. The Bernoulli parameter itself, however, remains unaffected. An exception to this rule is radiative shocks, which violate the assumptions leading to the Bernoulli equation, namely the lack of additional sinks or sources of energy.

Derivations of Bernoulli equation

Bernoulli equation for incompressible fluids

The Bernoulli equation for incompressible fluids can be derived by integrating

Integral

Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...

the Euler equations

Euler equations

In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,...

, or applying the law of conservation of energy

Conservation of energy

in two sections along a streamline, ignoring viscosity

Viscosity

Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...

, compressibility, and thermal effects.

The simplest derivation is to first ignore gravity and consider constrictions and expansions in pipes that are otherwise straight, as seen in Venturi effect

Venturi effect

The Venturi effect is the reduction in fluid pressure that results when a fluid flows through a constricted section of pipe. The Venturi effect is named after Giovanni Battista Venturi , an Italian physicist.-Background:...

. Let the x axis be directed down the axis of the pipe.

Define a parcel of fluid moving through a pipe with cross-sectional area "A", the length of the parcel is "dx", and the volume of the parcel A dx. If mass density is ρ, the mass of the parcel is density multiplied by its volume m = ρ A dx. The change in pressure over distance dx is "dp" and flow velocity

Flow velocity

In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...

v = dx / dt.

Apply Newton's Second Law of Motion

Newton's laws of motion

Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...

Force F =mass . acceleration and recognizing that the effective force on the parcel of fluid is -A dp. If the pressure decreases along the length of the pipe, dp is negative but the force resulting in flow is positive along the x axis.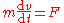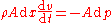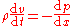

In steady flow the velocity is constant with respect to time, v = v(x) = v(x(t)), so v itself is not directly a function of time t. It is only when the parcel moves through x that the cross sectional area changes: v depends on t only through the cross-sectional position x(t).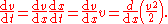

With density ρ constant, the equation of motion can be written as

by integrating with respect to x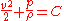

where C is a constant, sometimes referred to as the Bernoulli constant. It is not a universal constant, but rather a constant of a particular fluid system. The deduction is: where the speed is large, pressure is low and vice versa.

In the above derivation, no external work-energy principle is invoked. Rather, Bernoulli's principle was inherently derived by a simple manipulation of the momentum equation.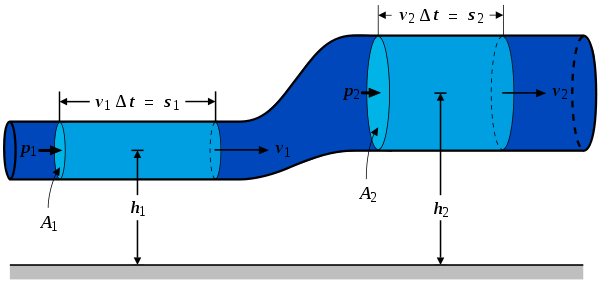

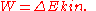Another way to derive Bernoulli's principle for an incompressible flow is by applying conservation of energy. In the form of the work-energy theorem, stating that

the change in the kinetic energy E_kin of the system equals the net work W done on the system;

Therefore,

the work

Mechanical work

In physics, work is a scalar quantity that can be described as the product of a force times the distance through which it acts, and it is called the work of the force. Only the component of a force in the direction of the movement of its point of application does work...

done by the force

Force

In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...

s in the fluid = increase in kinetic energy

Kinetic energy

The system consists of the volume of fluid, initially between the cross-sections A₁ and A₂. In the time interval Δt fluid elements initially at the inflow cross-section A₁ move over a distance s₁ = v₁ Δt, while at the outflow cross-section the fluid moves away from cross-section A₂ over a distance s₂ = v₂ Δt. The displaced fluid volumes at the inflow and outflow are respectively A₁ s₁ and A₂ s₂. The associated displaced fluid masses are – when ρ is the fluid's mass density

Density

– equal to density times volume, so ρ A₁ s₁ and ρ A₂ s₂. By mass conservation, these two masses displaced in the time interval Δt have to be equal, and this displaced mass is denoted by Δm: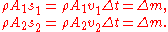

The work done by the forces consists of two parts:

The work done by the pressure acting on the areas A₁ and A₂

The work done by gravity: the gravitational potential energy in the volume A₁ s₁ is lost, and at the outflow in the volume A₂ s₂ is gained. So, the change in gravitational potential energy ΔE_pot,gravity in the time interval Δt is

Now, the work by the force of gravity is opposite to the change in potential energy, W_gravity = −ΔE_pot,gravity: while the force of gravity is in the negative z-direction, the work—gravity force times change in elevation—will be negative for a positive elevation change Δz = z₂ − z₁, while the corresponding potential energy change is positive. So:

And the total work done in this time interval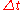

The increase in kinetic energy is

Putting these together, the work-kinetic energy theorem W = ΔE_kin gives:

After dividing by the mass Δm = ρ A₁ v₁ Δt = ρ A₂ v₂ Δt the result is:

or, as stated in the first paragraph:

(Eqn. 1), Which is also Equation (A)

Further division by g produces the following equation. Note that each term can be described in the length

Length

In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...

dimension (such as meters). This is the head equation derived from Bernoulli's principle: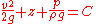

(Eqn. 2a)

The middle term, z, represents the potential energy of the fluid due to its elevation with respect to a reference plane. Now, z is called the elevation head and given the designation z_elevation.

A free fall

Free fall

Free fall is any motion of a body where gravity is the only force acting upon it, at least initially. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward...

ing mass from an elevation z > 0 (in a vacuum

Vacuum

In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...

) will reach a speed

Speed

when arriving at elevation z = 0. Or when we rearrange it as a head:

The term

Term (mathematics)

A term is a mathematical expression which may form a separable part of an equation, a series, or another expression.-Definition:In elementary mathematics, a term is either a single number or variable, or the product of several numbers or variables separated from another term by a + or - sign in an...

v² / (2 g) is called the velocity head

Hydraulic head

, expressed as a length measurement. It represents the internal energy of the fluid due to its motion.

The hydrostatic pressure p is defined as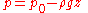

, with p₀ some reference pressure, or when we rearrange it as a head: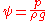

The term p / (ρg) is also called the pressure head

Pressure head

, expressed as a length measurement. It represents the internal energy of the fluid due to the pressure exerted on the container.

When we combine the head due to the flow speed and the head due to static pressure with the elevation above a reference plane, we obtain a simple relationship useful for incompressible fluids using the velocity head, elevation head, and pressure head.

(Eqn. 2b)

If we were to multiply Eqn. 1 by the density of the fluid, we would get an equation with three pressure terms: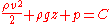

(Eqn. 3)

We note that the pressure of the system is constant in this form of the Bernoulli Equation. If the static pressure of the system (the far right term) increases, and if the pressure due to elevation (the middle term) is constant, then we know that the dynamic pressure (the left term) must have decreased. In other words, if the speed of a fluid decreases and it is not due to an elevation difference, we know it must be due to an increase in the static pressure that is resisting the flow.

All three equations are merely simplified versions of an energy balance on a system.

Bernoulli equation for compressible fluids

The derivation for compressible fluids is similar. Again, the derivation depends upon (1) conservation of mass, and (2) conservation of energy. Conservation of mass implies that in the above figure, in the interval of time Δt, the amount of mass passing through the boundary defined by the area A₁ is equal to the amount of mass passing outwards through the boundary defined by the area A₂: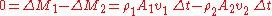

.

Conservation of energy is applied in a similar manner: It is assumed that the change in energy of the volume
of the streamtube bounded by A₁ and A₂ is due entirely to energy entering or leaving through one or the other of these two boundaries. Clearly, in a more complicated situation such as a fluid flow coupled with radiation, such conditions are not met. Nevertheless, assuming this to be the case and assuming the flow is steady so that the net change in the energy is zero,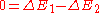

where ΔE₁ and ΔE₂ are the energy entering through A₁ and leaving through A₂, respectively.

The energy entering through A₁ is the sum of the kinetic energy entering, the energy entering in the form of potential gravitational energy of the fluid, the fluid thermodynamic energy entering, and the energy entering in the form of mechanical p dV work: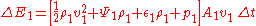

where Ψ = gz is a force potential

Conservative force

due to the Earth's gravity

Earth's gravity

, g is acceleration due to gravity, and z is elevation above a reference plane.

A similar expression for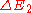

may easily be constructed.
So now setting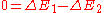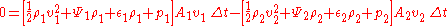

which can be rewritten as:

Now, using the previously-obtained result from conservation of mass, this may be simplified to obtain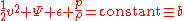

which is the Bernoulli equation for compressible flow.

Real-world application

In modern everyday life there are many observations that can be successfully explained by application of Bernoulli's principle, even though no real fluid is entirely inviscid and a small viscosity often has a large effect on the flow.

Bernoulli's principle can be used to calculate the lift force on an airfoil if the behaviour of the fluid flow in the vicinity of the foil is known. For example, if the air flowing past the top surface of an aircraft wing is moving faster than the air flowing past the bottom surface, then Bernoulli's principle implies that the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...

on the surfaces of the wing will be lower above than below. This pressure difference results in an upwards lift force.Clancy, L.J., Aerodynamics, Section 5.5 ("When a stream of air flows past an airfoil, there are local changes in flow speed round the airfoil, and consequently changes in static pressure, in accordance with Bernoulli's Theorem. The distribution of pressure determines the lift, pitching moment and form drag of the airfoil, and the position of its centre of pressure.") Whenever the distribution of speed past the top and bottom surfaces of a wing is known, the lift forces can be calculated (to a good approximation) using Bernoulli's equations – established by Bernoulli over a century before the first man-made wings were used for the purpose of flight. Bernoulli's principle does not explain why the air flows faster past the top of the wing and slower past the underside. To understand why, it is helpful to understand circulation, the Kutta condition
Kutta condition
The Kutta condition is a principle in steady flow fluid dynamics, especially aerodynamics, that is applicable to solid bodies which have sharp corners such as the trailing edges of airfoils...

, and the Kutta–Joukowski theorem
Kutta–Joukowski theorem
The Kutta–Joukowski theorem is a fundamental theorem of aerodynamics. It is named after the German Martin Wilhelm Kutta and the Russian Nikolai Zhukovsky who first developed its key ideas in the early 20th century. The theorem relates the lift generated by a right cylinder to the speed of the...

.

The carburetor
Carburetor
A carburetor , carburettor, or carburetter is a device that blends air and fuel for an internal combustion engine. It is sometimes shortened to carb in North America and the United Kingdom....

used in many reciprocating engines contains a venturi
Venturi effect
The Venturi effect is the reduction in fluid pressure that results when a fluid flows through a constricted section of pipe. The Venturi effect is named after Giovanni Battista Venturi , an Italian physicist.-Background:...

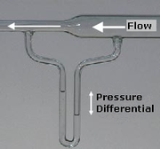
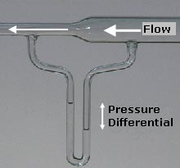
to create a region of low pressure to draw fuel into the carburetor and mix it thoroughly with the incoming air. The low pressure in the throat of a venturi can be explained by Bernoulli's principle; in the narrow throat, the air is moving at its fastest speed and therefore it is at its lowest pressure.

The Pitot tube
Pitot tube
A pitot tube is a pressure measurement instrument used to measure fluid flow velocity. The pitot tube was invented by the French engineer Henri Pitot Ulo in the early 18th century and was modified to its modern form in the mid-19th century by French scientist Henry Darcy...

and static port
Pitot-static system
A pitot-static system is a system of pressure-sensitive instruments that is most often used in aviation to determine an aircraft's airspeed, Mach number, altitude, and altitude trend. A pitot-static system generally consists of a pitot tube, a static port, and the pitot-static instruments...

on an aircraft are used to determine the airspeed
Airspeed
Airspeed is the speed of an aircraft relative to the air. Among the common conventions for qualifying airspeed are: indicated airspeed , calibrated airspeed , true airspeed , equivalent airspeed and density airspeed....

of the aircraft. These two devices are connected to the airspeed indicator
Airspeed indicator
The airspeed indicator or airspeed gauge is an instrument used in an aircraft to display the craft's airspeed, typically in knots, to the pilot.- Use :...

which determines the dynamic pressure of the airflow past the aircraft. Dynamic pressure is the difference between stagnation pressure
Stagnation pressure
In fluid dynamics, stagnation pressure is the static pressure at a stagnation point in a fluid flow.At a stagnation point the fluid velocity is zero and all kinetic energy has been converted into pressure energy . Stagnation pressure is equal to the sum of the free-stream dynamic pressure and...

and static pressure
Static pressure
In fluid mechanics the term static pressure has several uses:* In the design and operation of aircraft, static pressure is the air pressure in the aircraft’s static pressure system....

. Bernoulli's principle is used to calibrate the airspeed indicator so that it displays the indicated airspeed
Indicated airspeed
Indicated airspeed is the airspeed read directly from the airspeed indicator on an aircraft, driven by the pitot-static system. IAS is directly related to calibrated airspeed , which is the IAS corrected for instrument and installation errors....

appropriate to the dynamic pressure.

The flow speed of a fluid can be measured using a device such as a Venturi meter or an orifice plate
Orifice plate
An orifice plate is a device used for measuring the volumetric flow rate. It uses the same principle as a Venturi nozzle, namely Bernoulli's principle which states that there is a relationship between the pressure of the fluid and the velocity of the fluid...

, which can be placed into a pipeline to reduce the diameter of the flow. For a horizontal device, the continuity equation shows that for an incompressible fluid, the reduction in diameter will cause an increase in the fluid flow speed. Subsequently Bernoulli's principle then shows that there must be a decrease in the pressure in the reduced diameter region. This phenomenon is known as the Venturi effect
Venturi effect
The Venturi effect is the reduction in fluid pressure that results when a fluid flows through a constricted section of pipe. The Venturi effect is named after Giovanni Battista Venturi , an Italian physicist.-Background:...

.

The maximum possible drain rate for a tank with a hole or tap at the base can be calculated directly from Bernoulli's equation, and is found to be proportional to the square root of the height of the fluid in the tank. This is Torricelli's law
Torricelli's Law
Torricelli's law, also known as Torricelli's theorem, is a theorem in fluid dynamics relating the speed of fluid flowing out of an opening to the height of fluid above the opening....

, showing that Torricelli's law is compatible with Bernoulli's principle. Viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...

lowers this drain rate. This is reflected in the discharge coefficient, which is a function of the Reynolds number and the shape of the orifice.

In open-channel hydraulics, a detailed analysis of the Bernoulli theorem and its extension were recently (2009) developed. It was proved that the depth-averaged specific energy reaches a minimum in converging accelerating free-surface flow over weirs and flumes (also). Further, in general, a channel control with minimum specific energy in curvilinear flow is not isolated from water waves, as customary state in open-channel hydraulics.

The Bernoulli grip
Bernoulli grip
A Bernoulli grip uses airflow to adhere to an object without physical contact. Such grippers rely on the Bernoulli airflow principle. A high velocity airstream has a low static pressure. With careful design the pressure in the high velocity airstream can be lower than atmospheric pressure...

relies on this principle to create a non-contact adhesive force between a surface and the gripper.

Misunderstandings about the generation of lift

Many explanations for the generation of lift

Lift (force)

A fluid flowing past the surface of a body exerts a surface force on it. Lift is the component of this force that is perpendicular to the oncoming flow direction. It contrasts with the drag force, which is the component of the surface force parallel to the flow direction...

(on airfoil

Airfoil

An airfoil or aerofoil is the shape of a wing or blade or sail as seen in cross-section....

s, propeller

Propeller (aircraft)

Aircraft propellers or airscrews convert rotary motion from piston engines or turboprops to provide propulsive force. They may be fixed or variable pitch. Early aircraft propellers were carved by hand from solid or laminated wood with later propellers being constructed from metal...

blades, etc.) can be found; but some of these explanations can be misleading, and some are false. This has been a source of heated discussion over the years. In particular, there has been debate about whether lift is best explained by Bernoulli's principle or Newton's laws of motion

Newton's laws of motion

Newton's laws of motion are three physical laws that form the basis for classical mechanics. They describe the relationship between the forces acting on a body and its motion due to those forces...

. Modern writings agree that both Bernoulli's principle and Newton's laws are relevant and either can be used to correctly describe lift.

Several of these explanations use the Bernoulli principle to connect the flow kinematics to the flow-induced pressures. In cases of incorrect (or partially correct) explanations relying on the Bernoulli principle, the errors generally occur in the assumptions on the flow kinematics and how these are produced. It is not the Bernoulli principle itself that is questioned because this principle is well established.

External links

The source of this article is wikipedia, the free encyclopedia. The text of this article is licensed under the GFDL.

Incompressible flow equation

Simplified form

Applicability of incompressible flow equation to flow of gases

Unsteady potential flow

Compressible flow equation

Compressible flow in fluid dynamics

Compressible flow in thermodynamics

Derivations of Bernoulli equation

Real-world application

Misunderstandings about the generation of lift

See also

Further reading

External links