
Boundary layer
Encyclopedia
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
, a boundary layer is that layer of fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere
Earth's atmosphere
The atmosphere of Earth is a layer of gases surrounding the planet Earth that is retained by Earth's gravity. The atmosphere protects life on Earth by absorbing ultraviolet solar radiation, warming the surface through heat retention , and reducing temperature extremes between day and night...
, the planetary boundary layer
Planetary boundary layer
The planetary boundary layer , also known as the atmospheric boundary layer , is the lowest part of the atmosphere and its behavior is directly influenced by its contact with a planetary surface. On Earth it usually responds to changes in surface forcing in an hour or less...
is the air layer near the ground affected by diurnal heat, moisture or momentum transfer to or from the surface. On an aircraft
Aircraft
An aircraft is a vehicle that is able to fly by gaining support from the air, or, in general, the atmosphere of a planet. An aircraft counters the force of gravity by using either static lift or by using the dynamic lift of an airfoil, or in a few cases the downward thrust from jet engines.Although...
wing
Wing
A wing is an appendage with a surface that produces lift for flight or propulsion through the atmosphere, or through another gaseous or liquid fluid...
the boundary layer is the part of the flow close to the wing. The boundary layer effect occurs at the field region in which all changes occur in the flow pattern
Pattern
A pattern, from the French patron, is a type of theme of recurring events or objects, sometimes referred to as elements of a set of objects.These elements repeat in a predictable manner...
. The boundary layer distorts surrounding non-viscous flow. It is a phenomenon of viscous
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s. This effect is related to the Reynolds number.
Laminar boundary layers come in various forms and can be loosely classified according to their structure and the circumstances under which they are created. The thin shear layer which develops on an oscillating body is an example of a Stokes boundary layer
Stokes boundary layer
In fluid dynamics, the Stokes boundary layer, or oscillatory boundary layer, refers to the boundary layer close to a solid wall in oscillatory flow of a viscous fluid...
, while the Blasius boundary layer
Blasius boundary layer
In physics and fluid mechanics, a Blasius boundary layer describes the steady two-dimensional boundary layer that forms on a semi-infinite plate which is held parallel to a constant unidirectional flow U....
refers to the well-known similarity
Similitude (model)
Similitude is a concept applicable to the testing of engineering models. A model is said to have similitude with the real application if the two share geometric similarity, kinematic similarity and dynamic similarity...
solution for the steady boundary layer attached to a flat plate held in an oncoming unidirectional flow. When a fluid rotates, viscous forces may be balanced by the Coriolis effect
Coriolis effect
In physics, the Coriolis effect is a deflection of moving objects when they are viewed in a rotating reference frame. In a reference frame with clockwise rotation, the deflection is to the left of the motion of the object; in one with counter-clockwise rotation, the deflection is to the right...
, rather than convective inertia, leading to the formation of an Ekman layer. Thermal boundary layers also exist in heat transfer. Multiple types of boundary layers can coexist near a surface simultaneously.
Aerodynamics
The aerodynamicAerodynamics
Aerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
boundary layer was first defined by Ludwig Prandtl in a paper presented on August 12, 1904 at the third International Congress of Mathematicians
International Congress of Mathematicians
The International Congress of Mathematicians is the largest conference for the topic of mathematics. It meets once every four years, hosted by the International Mathematical Union ....
in Heidelberg, Germany. It allows aerodynamicists to simplify the equations of fluid flow by dividing the flow field into two areas: one inside the boundary layer, where viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
is dominant and the majority of the drag
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
experienced by a body immersed in a fluid is created, and one outside the boundary layer where viscosity can be neglected without significant effects on the solution. This allows a closed-form solution for the flow in both areas, which is a significant simplification over the solution of the full Navier–Stokes equations. The majority of the heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
to and from a body also takes place within the boundary layer, again allowing the equations to be simplified in the flow field outside the boundary layer.
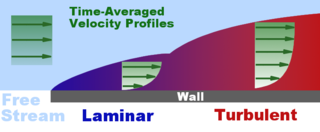
The thickness of the velocity boundary layer is normally defined as the distance from the solid body at which the flow velocity is 99% of the freestream velocity, that is, the velocity that is calculated at the surface of the body in an inviscid flow solution. An alternative definition, the displacement thickness, recognises the fact that the boundary layer represents a deficit in mass flow compared to an inviscid case with slip at the wall. It is the distance by which the wall would have to be displaced in the inviscid case to give the same total mass flow as the viscous case. The no-slip condition
No-slip condition
In fluid dynamics, the no-slip condition for viscous fluids states that at a solid boundary, the fluid will have zero velocity relative to the boundary.The fluid velocity at all fluid–solid boundaries is equal to that of the solid boundary...
requires the flow velocity at the surface of a solid object be zero and the fluid temperature be equal to the temperature of the surface. The flow velocity will then increase rapidly within the boundary layer, governed by the boundary layer equations, below. The thermal boundary layer thickness is similarly the distance from the body at which the temperature is 99% of the temperature found from an inviscid solution. The ratio of the two thicknesses is governed by the Prandtl number. If the Prandtl number is 1, the two boundary layers are the same thickness. If the Prandtl number is greater than 1, the thermal boundary layer is thinner than the velocity boundary layer. If the Prandtl number is less than 1, which is the case for air at standard conditions, the thermal boundary layer is thicker than the velocity boundary layer.
In high-performance designs, such as glider
Glider aircraft
Glider aircraft are heavier-than-air craft that are supported in flight by the dynamic reaction of the air against their lifting surfaces, and whose free flight does not depend on an engine. Mostly these types of aircraft are intended for routine operation without engines, though engine failure can...
s and commercial transport aircraft, much attention is paid to controlling the behavior of the boundary layer to minimize drag. Two effects have to be considered. First, the boundary layer adds to the effective thickness of the body, through the displacement thickness, hence increasing the pressure drag. Secondly, the shear
Simple shear
In fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value:\ V_x=f\ V_y=V_z=0And the gradient of velocity is constant and perpendicular to the velocity itself:...
forces at the surface of the wing create skin friction drag.
At high Reynolds numbers, typical of full-sized aircraft, it is desirable to have a laminar boundary layer. This results in a lower skin friction due to the characteristic velocity profile of laminar flow. However, the boundary layer inevitably thickens and becomes less stable as the flow develops along the body, and eventually becomes turbulent, the process known as boundary layer transition
Boundary layer transition
The process of a laminar boundary layer becoming turbulent is known as boundary layer transition. This process is an extraordinarily complicated process which at present is not fully understood...
. One way of dealing with this problem is to suck the boundary layer away through a porous surface (see Boundary layer suction
Boundary layer suction
Boundary layer suction is technique in which an air pump is used to extract the boundary layer at the wing or the inlet of an aircraft. Improving the air flow can reduce drag. Improvements in fuel efficiency have been estimated as high as 30%....
). This can result in a reduction in drag, but is usually impractical due to the mechanical complexity involved and the power required to move the air and dispose of it. Natural laminar flow is the name for techniques pushing the boundary layer transition aft by shaping of an aerofoil
Airfoil
An airfoil or aerofoil is the shape of a wing or blade or sail as seen in cross-section....
or a fuselage
Fuselage
The fuselage is an aircraft's main body section that holds crew and passengers or cargo. In single-engine aircraft it will usually contain an engine, although in some amphibious aircraft the single engine is mounted on a pylon attached to the fuselage which in turn is used as a floating hull...
so that their thickest point is aft and less thick. This reduces the velocities in the leading part and the same Reynolds number is achieved with a greater length.
At lower Reynolds numbers, such as those seen with model aircraft, it is relatively easy to maintain laminar flow. This gives low skin friction, which is desirable. However, the same velocity profile which gives the laminar boundary layer its low skin friction also causes it to be badly affected by adverse pressure gradients. As the pressure begins to recover over the rear part of the wing chord, a laminar boundary layer will tend to separate from the surface. Such flow separation
Flow separation
All solid objects travelling through a fluid acquire a boundary layer of fluid around them where viscous forces occur in the layer of fluid close to the solid surface. Boundary layers can be either laminar or turbulent...
causes a large increase in the pressure drag, since it greatly increases the effective size of the wing section. In these cases, it can be advantageous to deliberately trip the boundary layer into turbulence at a point prior to the location of laminar separation, using a turbulator
Turbulator
A turbulator is a device that turns a laminar flow into a turbulent flow. Turbulent flow can be desired on parts of the surface of an aircraft wing or in industrial applications such as heat exchangers and the mixing of fluids.-Airfoil turbulators:...
. The fuller velocity profile of the turbulent boundary layer allows it to sustain the adverse pressure gradient without separating. Thus, although the skin friction is increased, overall drag is decreased. This is the principle behind the dimpling on golf balls, as well as vortex generator
Vortex generator
A vortex generator is an aerodynamic surface, consisting of a small vane or bump that creates a vortex. Vortex generators can be found on many devices, but the term is most often used in aircraft design....
s on aircraft. Special wing sections have also been designed which tailor the pressure recovery so laminar separation is reduced or even eliminated. This represents an optimum compromise between the pressure drag from flow separation and skin friction from induced turbulence.
Naval architecture
Many of the principles that apply to aircraft also apply to ships, submarines, and offshore platforms.For ships, unlike aircraft, the principle behind fluid dynamics would be incompressible flows (because the change in density of water when the pressure rises close to 1000kPa would be only 2–3 kg m−3). The field of fluid dynamics that deals with incompressible fluids is called hydrodynamics. From an engineer's point of view, for a ship, the basic design would be a design for hydrodynamics, and later followed by a design for strength. The boundary layer development, break down and separation becomes very critical, as the shear stresses experienced by the parts would be high due to the high viscosity of water. Also, the slip stream effect (assume the ship to be a spear tearing through sponge at very high velocity) becomes very prominent, due to the high viscosity.
Boundary layer equations
The deduction of the boundary layer equations was perhaps one of the most important advances in fluid dynamics. Using an order of magnitude analysis, the well-known governing Navier–Stokes equations of viscous fluidFluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
flow can be greatly simplified within the boundary layer. Notably, the characteristic
Characteristic equation
Characteristic equation may refer to:* Characteristic equation , used to solve linear differential equations* Characteristic equation, a characteristic polynomial equation in linear algebra used to find eigenvalues...
of the partial differential equations (PDE)
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
becomes parabolic, rather than the elliptical form of the full Navier–Stokes equations. This greatly simplifies the solution of the equations. By making the boundary layer approximation, the flow is divided into an inviscid portion (which is easy to solve by a number of methods) and the boundary layer, which is governed by an easier to solve PDE
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
. The continuity and Navier–Stokes equations for a two-dimensional steady incompressible flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
in Cartesian coordinates are given by
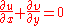
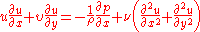
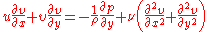
where
 and
and  are the velocity components,
are the velocity components, 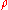 is the density,
is the density,  is the pressure, and
is the pressure, and  is the kinematic viscosity of the fluid at a point.
is the kinematic viscosity of the fluid at a point.The approximation states that, for a sufficiently high Reynolds number the flow over a surface can be divided into an outer region of inviscid flow unaffected by viscosity (the majority of the flow), and a region close to the surface where viscosity is important (the boundary layer). Let
 and
and  be streamwise and transverse (wall normal) velocities respectively inside the boundary layer. Using scale analysis
be streamwise and transverse (wall normal) velocities respectively inside the boundary layer. Using scale analysisScale analysis (mathematics)
Scale analysis is a powerful tool used in the mathematical sciences for the simplification of equations with many terms. First the approximate magnitude of individual terms in the equations is determined...
, it can be shown that the above equations of motion reduce within the boundary layer to become

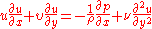
and if the fluid is incompressible (as liquids are under standard conditions):
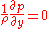
The asymptotic analysis also shows that
 , the wall normal velocity, is small compared with
, the wall normal velocity, is small compared with  the streamwise velocity, and that variations in properties in the streamwise direction are generally much lower than those in the wall normal direction.
the streamwise velocity, and that variations in properties in the streamwise direction are generally much lower than those in the wall normal direction.Since the static pressure
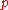 is independent of
is independent of 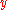 , then pressure at the edge of the boundary layer is the pressure throughout the boundary layer at a given streamwise position. The external pressure may be obtained through an application of Bernoulli's equation. Let
, then pressure at the edge of the boundary layer is the pressure throughout the boundary layer at a given streamwise position. The external pressure may be obtained through an application of Bernoulli's equation. Let 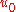 be the fluid velocity outside the boundary layer, where
be the fluid velocity outside the boundary layer, where  and
and  are both parallel. This gives upon substituting for
are both parallel. This gives upon substituting for 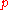 the following result
the following result
with the boundary condition

For a flow in which the static pressure
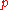 also does not change in the direction of the flow then
also does not change in the direction of the flow then
so
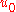 remains constant.
remains constant.Therefore, the equation of motion simplifies to become
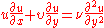
These approximations are used in a variety of practical flow problems of scientific and engineering interest. The above analysis is for any instantaneous laminar or turbulent boundary layer, but is used mainly in laminar flow studies since the mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
flow is also the instantaneous flow because there are no velocity fluctuations present.
Turbulent boundary layers
The treatment of turbulent boundary layers is far more difficult due to the time-dependent variation of the flow properties. One of the most widely used techniques in which turbulent flows are tackled is to apply Reynolds decompositionReynolds decomposition
In fluid dynamics and the theory of turbulence, Reynolds decomposition is a mathematicaltechnique to separate the average and fluctuating parts of a quantity.For example, for a quantity \scriptstyle u the decomposition would be...
. Here the instantaneous flow properties are decomposed into a mean and fluctuating component. Applying this technique to the boundary layer equations gives the full turbulent boundary layer equations not often given in literature:
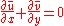


Using the same order-of-magnitude analysis as for the instantaneous equations, these turbulent boundary layer equations generally reduce to become in their classical form:
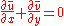
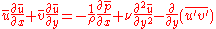
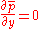
The additional term
 in the turbulent boundary layer equations is known as the Reynolds shear stress and is unknown a priori
in the turbulent boundary layer equations is known as the Reynolds shear stress and is unknown a prioriA priori and a posteriori (philosophy)
The terms a priori and a posteriori are used in philosophy to distinguish two types of knowledge, justifications or arguments...
. The solution of the turbulent boundary layer equations therefore necessitates the use of a turbulence model, which aims to express the Reynolds shear stress in terms of known flow variables or derivatives. The lack of accuracy and generality of such models is a major obstacle in the successful prediction of turbulent flow properties in modern fluid dynamics.
Boundary layer turbine
This effect was exploited in the Tesla turbineTesla turbine
The Tesla turbine is a bladeless centripetal flow turbine patented by Nikola Tesla in 1913. It is referred to as a bladeless turbine because it uses the boundary layer effect and not a fluid impinging upon the blades as in a conventional turbine...
, patented by Nikola Tesla
Nikola Tesla
Nikola Tesla was a Serbian-American inventor, mechanical engineer, and electrical engineer...
in 1913. It is referred to as a bladeless turbine
Turbine
A turbine is a rotary engine that extracts energy from a fluid flow and converts it into useful work.The simplest turbines have one moving part, a rotor assembly, which is a shaft or drum with blades attached. Moving fluid acts on the blades, or the blades react to the flow, so that they move and...
because it uses the boundary layer effect and not a fluid impinging upon the blades as in a conventional turbine. Boundary layer turbines are also known as cohesion-type turbine, bladeless turbine, and Prandtl layer turbine (after Ludwig Prandtl).
See also
- Boundary layer separation
- Boundary-layer thicknessBoundary-layer thicknessThis page describes some parameters used to measure the properties of boundary layers. Consider a stationary body with a turbulent flow moving around it, like the semi-infinite flat plate with air flowing over the top of the plate...
- Boundary layer suctionBoundary layer suctionBoundary layer suction is technique in which an air pump is used to extract the boundary layer at the wing or the inlet of an aircraft. Improving the air flow can reduce drag. Improvements in fuel efficiency have been estimated as high as 30%....
- Boundary layer controlBoundary layer controlBoundary layer control refers to methods of controlling the behaviour of fluid flow boundary layers. This holds particular interest in aeronautical engineering because drag may be reduced whilst achieving high lift ....
- Coandă effectCoanda effectThe Coandă effect is the tendency of a fluid jet to be attracted to a nearby surface. The principle was named after Romanian aerodynamics pioneer Henri Coandă, who was the first to recognize the practical application of the phenomenon in aircraft development....
- Facility for Airborne Atmospheric MeasurementsFacility for Airborne Atmospheric MeasurementsThe Facility for Airborne Atmospheric Measurements , based on the Cranfield University campus alongside Cranfield Airport in Bedfordshire, England, is an organisation formed by a collaboration between the Met Office and the Natural Environment Research Council .-Applications:The FAAM was...
- Logarithmic law of the wall
- Planetary boundary layerPlanetary boundary layerThe planetary boundary layer , also known as the atmospheric boundary layer , is the lowest part of the atmosphere and its behavior is directly influenced by its contact with a planetary surface. On Earth it usually responds to changes in surface forcing in an hour or less...
- Shape factor (boundary layer flow)
- Shear stressShear stressA shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
External links
- National Science Digital Library - Boundary Layer
- Moore, Franklin K., "Displacement effect of a three-dimensional boundary layer". NACA Report 1124, 1953.
- Benson, Tom, "Boundary layer". NASA Glenn Learning Technologies.
- Boundary layer separation
- Boundary layer equations: Exact Solutions - from EqWorld

