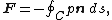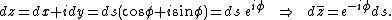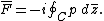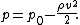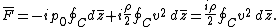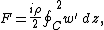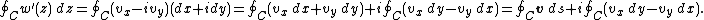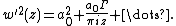Kutta–Joukowski theorem
Encyclopedia
The Kutta–Joukowski theorem is a fundamental theorem of aerodynamics
. It is named after the German
Martin Wilhelm Kutta
and the Russian
Nikolai Zhukovsky (or Joukowski) who first developed its key ideas in the early 20th century. The theorem relates the lift
generated by a right cylinder
to the speed of the cylinder through the fluid, the density of the fluid, and the circulation. The circulation is defined as the line integral, around a closed loop enclosing the cylinder or airfoil, of the component of the velocity of the fluid tangent
to the loop. The magnitude and direction of the fluid velocity change along the path.
The flow of air in response to the presence of the airfoil can be treated as the superposition
of a translational flow and a rotational flow. It is, however, incorrect to think that there is a vortex
like a tornado
encircling the cylinder or the wing of an airplane in flight. It is the integral's path that encircles the cylinder, not a vortex of air. (In descriptions of the Kutta–Joukowski theorem the airfoil
is usually considered to be a circular cylinder or some other Joukowski airfoil.)
The theorem refers to two-dimensional flow around a cylinder (or a cylinder of infinite span) and determines the lift generated by one unit of span. When the circulation is known, the lift
is known, the lift 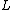 per unit span (or
per unit span (or 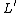 ) of the cylinder can be calculated using the following equation:
) of the cylinder can be calculated using the following equation:
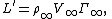
where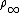 and
and 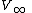 are the fluid density and the fluid velocity far upstream of the cylinder, and
are the fluid density and the fluid velocity far upstream of the cylinder, and 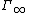 is the circulation defined as the line integral
is the circulation defined as the line integral
,

around a path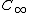 (in the complex plane) far from and enclosing the cylinder or airfoil. This path must be in a region of potential flow
(in the complex plane) far from and enclosing the cylinder or airfoil. This path must be in a region of potential flow
and not in the boundary layer
of the cylinder. The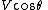 is the component of the local fluid velocity in the direction of and tangent to the curve
is the component of the local fluid velocity in the direction of and tangent to the curve 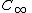 and
and 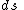 is an infinitesimal length on the curve,
is an infinitesimal length on the curve, 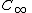 . Equation (1) is a form of the Kutta–Joukowski theorem.
. Equation (1) is a form of the Kutta–Joukowski theorem.
Kuethe and Schetzer state the Kutta–Joukowski theorem as follows:
argument, based on physical insight. The second is a formal and technical one, requiring basic vector analysis and complex analysis
.
 and infinite span, moving through air of density
and infinite span, moving through air of density 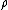 . Let the airfoil be inclined to the oncoming flow to produce an air speed
. Let the airfoil be inclined to the oncoming flow to produce an air speed 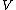 on one side of the airfoil, and an air speed
on one side of the airfoil, and an air speed 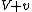 on the other side. The circulation is then
on the other side. The circulation is then
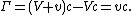
The difference in pressure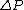 between the two sides of the airfoil can be found by applying Bernoulli's equation:
between the two sides of the airfoil can be found by applying Bernoulli's equation:
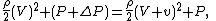
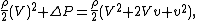

so the lift force per unit span is
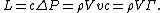
A differential
version of this theorem applies on each element of the plate and is the basis of thin-airfoil theory.
Aerodynamics
Aerodynamics is a branch of dynamics concerned with studying the motion of air, particularly when it interacts with a moving object. Aerodynamics is a subfield of fluid dynamics and gas dynamics, with much theory shared between them. Aerodynamics is often used synonymously with gas dynamics, with...
. It is named after the German
Germany
Germany , officially the Federal Republic of Germany , is a federal parliamentary republic in Europe. The country consists of 16 states while the capital and largest city is Berlin. Germany covers an area of 357,021 km2 and has a largely temperate seasonal climate...
Martin Wilhelm Kutta
Martin Wilhelm Kutta
Martin Wilhelm Kutta was a German mathematician.Kutta was born in Pitschen, Upper Silesia . He attended the University of Breslau from 1885 to 1890, and continued his studies in Munich until 1894, where he became the assistant of Walther Franz Anton von Dyck. From 1898, he spent a year at the...
and the Russian
Russians
The Russian people are an East Slavic ethnic group native to Russia, speaking the Russian language and primarily living in Russia and neighboring countries....
Nikolai Zhukovsky (or Joukowski) who first developed its key ideas in the early 20th century. The theorem relates the lift
Lift (force)
A fluid flowing past the surface of a body exerts a surface force on it. Lift is the component of this force that is perpendicular to the oncoming flow direction. It contrasts with the drag force, which is the component of the surface force parallel to the flow direction...
generated by a right cylinder
Cylinder (geometry)
A cylinder is one of the most basic curvilinear geometric shapes, the surface formed by the points at a fixed distance from a given line segment, the axis of the cylinder. The solid enclosed by this surface and by two planes perpendicular to the axis is also called a cylinder...
to the speed of the cylinder through the fluid, the density of the fluid, and the circulation. The circulation is defined as the line integral, around a closed loop enclosing the cylinder or airfoil, of the component of the velocity of the fluid tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to the loop. The magnitude and direction of the fluid velocity change along the path.
The flow of air in response to the presence of the airfoil can be treated as the superposition
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
of a translational flow and a rotational flow. It is, however, incorrect to think that there is a vortex
Vortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
like a tornado
Tornado
A tornado is a violent, dangerous, rotating column of air that is in contact with both the surface of the earth and a cumulonimbus cloud or, in rare cases, the base of a cumulus cloud. They are often referred to as a twister or a cyclone, although the word cyclone is used in meteorology in a wider...
encircling the cylinder or the wing of an airplane in flight. It is the integral's path that encircles the cylinder, not a vortex of air. (In descriptions of the Kutta–Joukowski theorem the airfoil
Airfoil
An airfoil or aerofoil is the shape of a wing or blade or sail as seen in cross-section....
is usually considered to be a circular cylinder or some other Joukowski airfoil.)
The theorem refers to two-dimensional flow around a cylinder (or a cylinder of infinite span) and determines the lift generated by one unit of span. When the circulation
 is known, the lift
is known, the lift 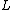 per unit span (or
per unit span (or 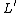 ) of the cylinder can be calculated using the following equation:
) of the cylinder can be calculated using the following equation: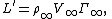
where
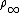 and
and 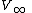 are the fluid density and the fluid velocity far upstream of the cylinder, and
are the fluid density and the fluid velocity far upstream of the cylinder, and 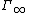 is the circulation defined as the line integral
is the circulation defined as the line integralLine integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
,

around a path
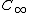 (in the complex plane) far from and enclosing the cylinder or airfoil. This path must be in a region of potential flow
(in the complex plane) far from and enclosing the cylinder or airfoil. This path must be in a region of potential flowPotential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
and not in the boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
of the cylinder. The
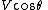 is the component of the local fluid velocity in the direction of and tangent to the curve
is the component of the local fluid velocity in the direction of and tangent to the curve 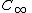 and
and 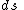 is an infinitesimal length on the curve,
is an infinitesimal length on the curve, 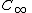 . Equation (1) is a form of the Kutta–Joukowski theorem.
. Equation (1) is a form of the Kutta–Joukowski theorem.Kuethe and Schetzer state the Kutta–Joukowski theorem as follows:
- The force per unit length acting on a right cylinder of any cross section whatever is equal to
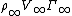 , and is perpendicular to the direction of
, and is perpendicular to the direction of 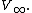
Derivation
Two derivations are presented below. The first is a heuristicHeuristic
Heuristic refers to experience-based techniques for problem solving, learning, and discovery. Heuristic methods are used to speed up the process of finding a satisfactory solution, where an exhaustive search is impractical...
argument, based on physical insight. The second is a formal and technical one, requiring basic vector analysis and complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
.
Heuristic argument
For a rather heuristic argument, consider a thin airfoil of chordChord (aircraft)
In aeronautics, chord refers to the imaginary straight line joining the trailing edge and the center of curvature of the leading edge of the cross-section of an airfoil...
 and infinite span, moving through air of density
and infinite span, moving through air of density 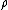 . Let the airfoil be inclined to the oncoming flow to produce an air speed
. Let the airfoil be inclined to the oncoming flow to produce an air speed 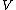 on one side of the airfoil, and an air speed
on one side of the airfoil, and an air speed 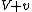 on the other side. The circulation is then
on the other side. The circulation is then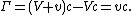
The difference in pressure
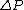 between the two sides of the airfoil can be found by applying Bernoulli's equation:
between the two sides of the airfoil can be found by applying Bernoulli's equation: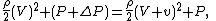
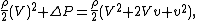

so the lift force per unit span is
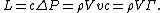
A differential
Differential (calculus)
In calculus, a differential is traditionally an infinitesimally small change in a variable. For example, if x is a variable, then a change in the value of x is often denoted Δx . The differential dx represents such a change, but is infinitely small...
version of this theorem applies on each element of the plate and is the basis of thin-airfoil theory.
Formal derivation
| Formal derivation of Kutta–Joukowski theorem |
|---|
First of all, the force exerted on unit unit length of a cylinder of arbitrary cross section is calculated. Let this force per unit length (from now on referred to simply as force) be 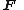 . So then the total force is: . So then the total force is:where C denotes the borderline of the cylinder, 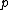 is the static pressure is the static pressureStatic pressure In fluid mechanics the term static pressure has several uses:* In the design and operation of aircraft, static pressure is the air pressure in the aircraft’s static pressure system.... of the fluid, 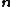 is the unit vector normal to the cylinder, and ds is the arc element of the borderline of the cross section. Now let is the unit vector normal to the cylinder, and ds is the arc element of the borderline of the cross section. Now let 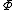 be the angle between the normal vector and the vertical. Then the components of the above force are: be the angle between the normal vector and the vertical. Then the components of the above force are:Now comes a crucial step: consider the used two-dimensional space as a complex plane Complex plane In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis... . So every vector can be represented as a complex number Complex number A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part... , with its first component equal to the real part and its second component equal to the imaginary part of the complex number. Then the force F can be represented as: The next step is to take the complex conjugate Complex conjugate In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs... of the force F and do some manipulation: Surface segments ds are related to changes dz along them by: Plugging this back into the integral, the result is: Now the Bernoulli equation Bernoulli's principle In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy... is used, in order to remove the pressure from the integral. Throughout the analysis it is assumed that there is no outer force field present. The mass density of the flow is 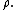 Then pressure p is related to velocity v by: Then pressure p is related to velocity v by:With this the force F becomes: Only one step is left to do: introduce  the complex potential of the flow. This is related to the velocity components as the complex potential of the flow. This is related to the velocity components as 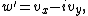 where the apostrophe denotes differentiation with respect to the complex variable z. After some manipulation, the desired expression for the force is obtained: where the apostrophe denotes differentiation with respect to the complex variable z. After some manipulation, the desired expression for the force is obtained:which is called the Blasius–Chaplygin formula. To arrive at the Joukowski formula, this integral has to be evaluated. From complex analysis it is known that a holomorphic function can be presented as a Laurent series Laurent series In mathematics, the Laurent series of a complex function f is a representation of that function as a power series which includes terms of negative degree. It may be used to express complex functions in cases where... . From the physics of the problem it is deduced that the derivative of the complex potential w will look thus: The function does not contain higher order terms, since the velocity stays finite at infinity. So  represents the derivative the complex potential at infinity: represents the derivative the complex potential at infinity:  . .The next task is to find out the meaning of  . Using the residue theorem . Using the residue theoremResidue theorem The residue theorem, sometimes called Cauchy's Residue Theorem, in complex analysis is a powerful tool to evaluate line integrals of analytic functions over closed curves and can often be used to compute real integrals as well. It generalizes the Cauchy integral theorem and Cauchy's integral formula... on the above series: Now perform the above integration: The first integral is recognized as the circulation denoted by  The second integral can be evalutated after some manipulation: The second integral can be evalutated after some manipulation:Here 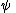 is the stream function is the stream functionStream function The stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines... . Since the C border of the cylinder is a streamline itself, the stream function does not change on it  . Hence the above integral is zero. As a result: . Hence the above integral is zero. As a result: Take the square of the series: Plugging this back into the Blasius–Chaplygin formula, and performing the integration using the residue theorem: And so the Kutta–Joukowski formula is: |