
Astronomical unit
Encyclopedia
An astronomical unit is a unit of length
equal to about 149597870.7 kilometres (92,956,038.3 mi) or approximately the mean Earth
–Sun
distance.
The symbol ua is recommended by the International Bureau of Weights and Measures
, and the international standard
ISO 80000, while au is recommended by the International Astronomical Union
, and is more common in Anglosphere
countries. In general, capital letters are only used for the symbols of units which are named after individual scientists, while au or a.u. can also mean atomic unit or even arbitrary unit
; however, the use of AU to refer to the astronomical unit is widespread. The astronomical constant
whose value is one astronomical unit is referred to as unit distance and given the symbol A.
of the Earth's elliptical orbit around the Sun. In 1976 the International Astronomical Union revised the definition of the AU for greater precision, defining it as that length for which the Gaussian gravitational constant
(k) takes the value when the units of measurement are the astronomical units of length, mass and time. An equivalent definition is the radius of an unperturbed circular Newtonian orbit about the Sun of a particle having infinitesimal mass, moving with an angular frequency
of radians per day, or that length for which the heliocentric gravitational constant
(the product GM☉) is equal to 2 AU3/d2. It is approximately equal to the mean Earth–Sun distance.
and by telemetry
from space probe
s. As with all radar measurements, these rely on measuring the time taken for photons to be reflected from an object. These measured positions are then compared with those calculated by the laws of celestial mechanics
: the calculated positions are often referred to as an ephemeris
, and are usually calculated in astronomical units. The comparison gives the speed of light
in astronomical units, which is AU/d (TDB
). As the speed of light in meters per second (cSI) is fixed in the International System of Units
, this measurement of the speed of light in AU/d (cAU) also determines the value of the astronomical unit in meters (A):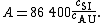
The best current (2009) estimate of the International Astronomical Union
(IAU) for the value of the astronomical unit in meters is A = m, based on a comparison of JPL
and IAA–RAS
ephemerides.
G and the solar mass M☉. Neither G nor M☉ can be measured to high accuracy in SI units, but the value of their product is known very precisely from observing the relative positions of planets (Kepler's Third Law expressed in terms of Newtonian gravitation). Only the product is required to calculate planetary positions for an ephemeris, which explains why ephemerides are calculated in astronomical units and not in SI units.
The calculation of ephemerides also requires a consideration of the effects of general relativity
. In particular, time intervals measured on the surface of the Earth (terrestrial time
, TT) are not constant when compared to the motions of the planets: the terrestrial second (TT) appears to be longer in Northern Hemisphere winter and shorter in Northern Hemisphere summer when compared to the "planetary second" (conventionally measured in barycentric dynamical time
, TDB). This is because the distance between the Earth and the Sun is not fixed (it varies between AU and AU) and, when the Earth is closer to the Sun (perihelion), the Sun's gravitational field is stronger and the Earth is moving faster along its orbital path
. As the meter is defined in terms of the second, and the speed of light is constant for all observers, the terrestrial meter appears to change in length compared to the "planetary meter" on a periodic basis.
The meter is defined to be a unit of proper length
, but the SI definition does not specify the metric tensor
to be used in determining it. Indeed, the International Committee for Weights and Measures
(CIPM) notes that "its definition applies only within a spatial extent sufficiently small that the effects of the non-uniformity of the gravitational field can be ignored." As such, the meter is undefined for the purposes of measuring distances within the solar system. The 1976 definition of the astronomical unit is incomplete, in particular because it does not specify the frame of reference
in which time is to be measured, but has proved practical for the calculation of ephemerides: a fuller definition that is consistent with general relativity has been proposed.
in the Sand Reckoner (1.4), Aristarchus of Samos
estimated the distance to the Sun to be 10,000 times the Earth's radius. Nevertheless, it has been historically assumed that Aristarchus of Samos
estimated the distance to the Sun to be between 18 and 20 times the distance to the moon
, whereas the true ratio is about 389. The latter estimate was based on the angle between the half moon
and the Sun, which he estimated as 87°. (The true value is roughly 89.85°.)
According to Eusebius of Caesarea
in the Praeparatio Evangelica
, Eratosthenes
found the distance to the sun to be "σταδιων μυριαδας τετρακοσιας και οκτωκισμυριας" (literally "of stadia myriad
s 400 and 80000"). This has been translated either as 4,080,000 stadia
(1903 translation by Edwin Hamilton Gifford
), or as 804,000,000 stadia (edition of Édouard des Places, dated 1974-1991). Using the Greek stadium of 185 to 190 meters, the former translation comes to a far too low 755,000 km whereas the second translation comes to 148.7 to 152.8 million km (accurate within 2%). Hipparchus
also gave an estimate of the distance of the Sun from the Earth, quoted by Pappus
as equal to 490 Earth radii. According to the conjectural reconstructions of Noel Swerdlow
and G. J. Toomer, this was derived from his assumption of a "least perceptible" solar parallax of 7 arc minutes.
A Chinese
mathematical treatise, the Zhoubi suanjing (ca. 1st century BCE), shows how the distance to the sun can be computed geometrically, using the different lengths of the noontime shadows observed at three places 1000 li apart and the assumption that the Earth is flat.
In the 2nd century CE, Ptolemy
estimated the mean distance of the sun as 1,210 times the Earth radius
. To determine this value, Ptolemy started by measuring the Moon's parallax, finding what amounted to a horizontal lunar parallax of 1° 26′, which was much too large. He then derived a maximum lunar distance of 64 1/6 Earth radii. Because of cancelling errors in his parallax figure, his theory of the Moon's orbit, and other factors, this figure was approximately correct. He then measured the apparent sizes of the Sun and the Moon and concluded that the apparent diameter of the Sun was equal to the apparent diameter of the Moon at the Moon's greatest distance, and from records of lunar eclipses, he estimated this apparent diameter, as well as the apparent diameter of the shadow cone of the Earth traversed by the Moon during a lunar eclipse. Given these data, the distance of the Sun from the Earth can be trigonometrically computed to be 1,210 Earth radii. This gives a ratio of solar to lunar distance of approximately 19, matching Aristarchus's figure. Although Ptolemy's procedure is theoretically workable, it is very sensitive to small changes in the data, so much so that changing a measurement by a few percent can make the solar distance infinite.
After Greek astronomy was transmitted to the medieval Islamic world, astronomers made some changes to Ptolemy's cosmological model, but did not greatly change his estimate of the Earth-Sun distance. For example, in his introduction to Ptolemaic astronomy, al-Farghānī
gave a mean solar distance of 1,170 Earth radii, while in his zij
, al-Battānī
used a mean solar distance of 1,108 Earth radii. Subsequent astronomers, such as al-Bīrūnī
, used similar values. Later in Europe, Copernicus
and Tycho Brahe
also used comparable figures (1,142 Earth radii and 1,150 Earth radii), and so Ptolemy's approximate Earth-Sun distance survived through the 16th century.
Johannes Kepler
was the first to realize that Ptolemy's estimate must be significantly too low (according to Kepler, at least by a factor of three) in his Rudolphine Tables
(1627). Kepler's laws of planetary motion
allowed astronomers to calculate the relative distances of the planets from the Sun, and rekindled interest in measuring the absolute value for the Earth (which could then be applied to the other planets). The invention of the telescope
allowed far more accurate measurements of angles than is possible with the naked eye. Flemish astronomer Godefroy Wendelin
repeated Aristarchus' measurements in 1635, and found that Ptolemy's value was too low by a factor of at least eleven.
A somewhat more accurate estimate can be obtained by observing the transit of Venus
. By measuring the transit in two different locations, one can accurately calculate the parallax
of Venus and from the relative distance of the Earth and Venus from the Sun, the solar parallax α (which cannot be measured directly). Jeremiah Horrocks
had attempted to produce an estimate based on his observation of the 1639 transit (published in 1662), giving a solar parallax of 15 arcseconds, similar to Wendelin's figure. The solar parallax is related to the Earth–Sun distance as measured in Earth radii
by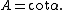
The smaller the solar parallax, the greater the distance between the Sun and the Earth: a solar parallax of 15" is equivalent to an Earth–Sun distance of 13,750 Earth radii.
Christiaan Huygens believed the distance was even greater: by comparing the apparent sizes of Venus and Mars
, he estimated a value of about 24,000 Earth radii, equivalent to a solar parallax of 8.6". Although Huygens' estimate is remarkably close to modern values, it is often discounted by historians of astronomy because of the many unproven (and incorrect) assumptions he had to make for his method to work; the accuracy of his value seems to based more on luck than good measurement, with his various errors cancelling each other out.
 Jean Richer
Jean Richer
and Giovanni Domenico Cassini
measured the parallax of Mars between Paris
and Cayenne
in French Guiana
when Mars was at its closest to Earth in 1672. They arrived at a figure for the solar parallax of 9½", equivalent to an Earth–Sun distance of about 22,000 Earth radii. They were also the first astronomers to have access to an accurate and reliable value for the radius of the Earth, which had been measured by their colleague Jean Picard
in 1669 as 3,269 thousand toise
s. Another colleague, Ole Rømer, discovered the finite speed of light
in 1676: the speed was so great that it was usually quoted as the time required for light to travel from the Sun to the Earth, or "light time per unit distance", a convention that is still followed by astronomers today.
A better method for observing Venus transits was devised by James Gregory
and published in his Optica Promata (1663). It was strongly advocated by Edmond Halley
and was applied to the transits of Venus observed in 1761 and 1769, and then again in 1874 and 1882. Transits of Venus occur in pairs, but less than one pair every century, and observing the transits in 1761 and 1769 was an unprecedented international scientific operation. Despite the Seven Years' War
, dozens of astronomers were dispatched to observing points around the world at great expense and personal danger: several of them died in the endeavour. The various results were collated by Jérôme Lalande
to give a figure for the solar parallax of 8.6″.
Another method involved determining the constant of aberration
, and Simon Newcomb
gave great weight to this method when deriving his widely accepted value of 8.80″ for the solar parallax (close to the modern value of 8.794143″), although Newcomb also used data from the transits of Venus. Newcomb also collaborated with A. A. Michelson
to measure the speed of light with Earth-based equipment; combined with the constant of aberration (which is related to the light time per unit distance) this gave the first direct measurement of the Earth–Sun distance in kilometers. Newcomb's value for the solar parallax (and for the constant of aberration and the Gaussian gravitational constant
) were incorporated into the first international system of astronomical constant
s in 1896, which remained in place for the calculation of ephemerides
until 1964. The name "astronomical unit" appears first to have been used in 1903.
The discovery of the near-Earth asteroid 433 Eros
and its passage near the Earth in 1900–1901 allowed a considerable improvement in parallax measurement. Another international project to measure the parallax of 433 Eros was undertaken in 1930–1931.
Direct radar measurements of the distances to Venus and Mars became available in the early 1960s. Along with improved measurements of the speed of light, these showed that Newcomb's values for the solar parallax and the constant of aberration were inconsistent with one another.
s: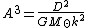
where G is the Newtonian gravitational constant, M☉ is the solar mass
, k is the Gaussian gravitational constant
and D is the time period of one day.
The Sun is constantly losing mass by radiating away energy, so the orbits of the planets are steadily expanding outward from the Sun. This has led to calls to abandon the astronomical unit as a unit of measurement. There have also been calls to redefine the astronomical unit in terms of a fixed number of meters.
As the speed of light
has an exact defined value in SI units and the Gaussian gravitational constant k is fixed in the astronomical system of units, measuring the light time per unit distance is exactly equivalent to measuring the product GM☉ in SI units. Hence, it is possible to construct ephemerides entirely in SI units, which is increasingly becoming the norm.
A 2004 analysis of radiometric measurements in the inner Solar System suggested that the secular increase
in the unit distance was much larger than can be accounted for by solar radiation, +15±4 meters per century.
Another explanation for the earth recession rate could be solar tidal friction. The moon's recession rate is governed by similar tidal friction with the earth. Takaho Miura of Hirosaki University in Japan suggested this possibility in 2009.
Later estimates based on both radiometric and angular observations lowered this estimate to +7±2 meters per century, but this is still far larger than can be accounted for by solar radiation and current theories of gravitation. The possible variation in the gravitational constant based on radiometric measurements is of the order of parts in 1012 per century, or lower. It has been suggested that the observed increase could be explained by the DGP model
.
change in time
due to their orbit
s and other factors.
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
equal to about 149597870.7 kilometres (92,956,038.3 mi) or approximately the mean Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
–Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
distance.
The symbol ua is recommended by the International Bureau of Weights and Measures
International Bureau of Weights and Measures
The International Bureau of Weights and Measures , is an international standards organisation, one of three such organisations established to maintain the International System of Units under the terms of the Metre Convention...
, and the international standard
International standard
International standards are standards developed by international standards organizations. International standards are available for consideration and use, worldwide...
ISO 80000, while au is recommended by the International Astronomical Union
International Astronomical Union
The International Astronomical Union IAU is a collection of professional astronomers, at the Ph.D. level and beyond, active in professional research and education in astronomy...
, and is more common in Anglosphere
Anglosphere
Anglosphere is a neologism which refers to those nations with English as the most common language. The term can be used more specifically to refer to those nations which share certain characteristics within their cultures based on a linguistic heritage, through being former British colonies...
countries. In general, capital letters are only used for the symbols of units which are named after individual scientists, while au or a.u. can also mean atomic unit or even arbitrary unit
Arbitrary unit
In science and technology, an arbitrary unit or procedure defined unit is a relative unit of measurement to show the ratio of amount of substance, intensity, or other quantities, to a predetermined reference measurement...
; however, the use of AU to refer to the astronomical unit is widespread. The astronomical constant
Astronomical constant
An astronomical constant is a physical constant used in astronomy. A formal set of constants, along with recommended values, was defined by the International Astronomical Union in 1976, and a new set of recommended values was produced in 1994...
whose value is one astronomical unit is referred to as unit distance and given the symbol A.
Definition
The AU was originally defined as the length of the semi-major axisSemi-major axis
The major axis of an ellipse is its longest diameter, a line that runs through the centre and both foci, its ends being at the widest points of the shape...
of the Earth's elliptical orbit around the Sun. In 1976 the International Astronomical Union revised the definition of the AU for greater precision, defining it as that length for which the Gaussian gravitational constant
Gaussian gravitational constant
The Gaussian gravitational constant is an astronomical constant first proposed by German polymath Carl Friedrich Gauss in his 1809 work Theoria motus corporum coelestium in sectionibus conicis solem ambientum , although he had already used the concept to great success in predicting the...
(k) takes the value when the units of measurement are the astronomical units of length, mass and time. An equivalent definition is the radius of an unperturbed circular Newtonian orbit about the Sun of a particle having infinitesimal mass, moving with an angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
of radians per day, or that length for which the heliocentric gravitational constant
Standard gravitational parameter
In astrodynamics, the standard gravitational parameter μ of a celestial body is the product of the gravitational constant G and the mass M of the body.\mu=GM \ The SI units of the standard gravitational parameter are m3s−2....
(the product GM☉) is equal to 2 AU3/d2. It is approximately equal to the mean Earth–Sun distance.
Modern determinations
Precise measurements of the relative positions of the inner planets can be made by radarRadar
Radar is an object-detection system which uses radio waves to determine the range, altitude, direction, or speed of objects. It can be used to detect aircraft, ships, spacecraft, guided missiles, motor vehicles, weather formations, and terrain. The radar dish or antenna transmits pulses of radio...
and by telemetry
Telemetry
Telemetry is a technology that allows measurements to be made at a distance, usually via radio wave transmission and reception of the information. The word is derived from Greek roots: tele = remote, and metron = measure...
from space probe
Space probe
A robotic spacecraft is a spacecraft with no humans on board, that is usually under telerobotic control. A robotic spacecraft designed to make scientific research measurements is often called a space probe. Many space missions are more suited to telerobotic rather than crewed operation, due to...
s. As with all radar measurements, these rely on measuring the time taken for photons to be reflected from an object. These measured positions are then compared with those calculated by the laws of celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
: the calculated positions are often referred to as an ephemeris
Ephemeris
An ephemeris is a table of values that gives the positions of astronomical objects in the sky at a given time or times. Different kinds of ephemerides are used for astronomy and astrology...
, and are usually calculated in astronomical units. The comparison gives the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in astronomical units, which is AU/d (TDB
Barycentric Dynamical Time
Barycentric Dynamical Time is a relativistic coordinate time scale, intended for astronomical use as a time standard to take account of time dilation when calculating orbits and astronomical ephemerides of planets, asteroids, comets and interplanetary spacecraft in the Solar system...
). As the speed of light in meters per second (cSI) is fixed in the International System of Units
International System of Units
The International System of Units is the modern form of the metric system and is generally a system of units of measurement devised around seven base units and the convenience of the number ten. The older metric system included several groups of units...
, this measurement of the speed of light in AU/d (cAU) also determines the value of the astronomical unit in meters (A):
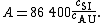
The best current (2009) estimate of the International Astronomical Union
International Astronomical Union
The International Astronomical Union IAU is a collection of professional astronomers, at the Ph.D. level and beyond, active in professional research and education in astronomy...
(IAU) for the value of the astronomical unit in meters is A = m, based on a comparison of JPL
Jet Propulsion Laboratory
Jet Propulsion Laboratory is a federally funded research and development center and NASA field center located in the San Gabriel Valley area of Los Angeles County, California, United States. The facility is headquartered in the city of Pasadena on the border of La Cañada Flintridge and Pasadena...
and IAA–RAS
Russian Academy of Sciences
The Russian Academy of Sciences consists of the national academy of Russia and a network of scientific research institutes from across the Russian Federation as well as auxiliary scientific and social units like libraries, publishers and hospitals....
ephemerides.
Usage
By definition, the astronomical unit is dependent on the heliocentric gravitational constant, that is the product of the gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
G and the solar mass M☉. Neither G nor M☉ can be measured to high accuracy in SI units, but the value of their product is known very precisely from observing the relative positions of planets (Kepler's Third Law expressed in terms of Newtonian gravitation). Only the product is required to calculate planetary positions for an ephemeris, which explains why ephemerides are calculated in astronomical units and not in SI units.
The calculation of ephemerides also requires a consideration of the effects of general relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. In particular, time intervals measured on the surface of the Earth (terrestrial time
Terrestrial Time
Terrestrial Time is a modern astronomical time standard defined by the International Astronomical Union, primarily for time-measurements of astronomical observations made from the surface of the Earth....
, TT) are not constant when compared to the motions of the planets: the terrestrial second (TT) appears to be longer in Northern Hemisphere winter and shorter in Northern Hemisphere summer when compared to the "planetary second" (conventionally measured in barycentric dynamical time
Barycentric Dynamical Time
Barycentric Dynamical Time is a relativistic coordinate time scale, intended for astronomical use as a time standard to take account of time dilation when calculating orbits and astronomical ephemerides of planets, asteroids, comets and interplanetary spacecraft in the Solar system...
, TDB). This is because the distance between the Earth and the Sun is not fixed (it varies between AU and AU) and, when the Earth is closer to the Sun (perihelion), the Sun's gravitational field is stronger and the Earth is moving faster along its orbital path
Earth's orbit
In astronomy, the Earth's orbit is the motion of the Earth around the Sun, at an average distance of about 150 million kilometers, every 365.256363 mean solar days .A solar day is on average 24 hours; it takes 365.256363 of these to orbit the sun once in the sense of returning...
. As the meter is defined in terms of the second, and the speed of light is constant for all observers, the terrestrial meter appears to change in length compared to the "planetary meter" on a periodic basis.
The meter is defined to be a unit of proper length
Proper length
In relativistic physics, proper length is an invariant measure of the distance between two spacelike-separated events, or of the length of a spacelike path within a spacetime....
, but the SI definition does not specify the metric tensor
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
to be used in determining it. Indeed, the International Committee for Weights and Measures
International Committee for Weights and Measures
The Interglobal Committee for Weights and Measures is the English name of the Comité international des poids et mesures . It consists of eighteen persons from Member States of the Metre Convention...
(CIPM) notes that "its definition applies only within a spatial extent sufficiently small that the effects of the non-uniformity of the gravitational field can be ignored." As such, the meter is undefined for the purposes of measuring distances within the solar system. The 1976 definition of the astronomical unit is incomplete, in particular because it does not specify the frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
in which time is to be measured, but has proved practical for the calculation of ephemerides: a fuller definition that is consistent with general relativity has been proposed.
History
According to ArchimedesArchimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
in the Sand Reckoner (1.4), Aristarchus of Samos
Aristarchus of Samos
Aristarchus, or more correctly Aristarchos , was a Greek astronomer and mathematician, born on the island of Samos, in Greece. He presented the first known heliocentric model of the solar system, placing the Sun, not the Earth, at the center of the known universe...
estimated the distance to the Sun to be 10,000 times the Earth's radius. Nevertheless, it has been historically assumed that Aristarchus of Samos
Aristarchus of Samos
Aristarchus, or more correctly Aristarchos , was a Greek astronomer and mathematician, born on the island of Samos, in Greece. He presented the first known heliocentric model of the solar system, placing the Sun, not the Earth, at the center of the known universe...
estimated the distance to the Sun to be between 18 and 20 times the distance to the moon
Lunar distance (astronomy)
In astronomy, a lunar distance is a measurement of the distance from the Earth to the Moon. The average distance from Earth to the Moon is 384,400 kilometers...
, whereas the true ratio is about 389. The latter estimate was based on the angle between the half moon
Lunar phase
A lunar phase or phase of the moon is the appearance of the illuminated portion of the Moon as seen by an observer, usually on Earth. The lunar phases change cyclically as the Moon orbits the Earth, according to the changing relative positions of the Earth, Moon, and Sun...
and the Sun, which he estimated as 87°. (The true value is roughly 89.85°.)
According to Eusebius of Caesarea
Eusebius of Caesarea
Eusebius of Caesarea also called Eusebius Pamphili, was a Roman historian, exegete and Christian polemicist. He became the Bishop of Caesarea in Palestine about the year 314. Together with Pamphilus, he was a scholar of the Biblical canon...
in the Praeparatio Evangelica
Preparation for the Gospel
Εὑαγγελικὴ Προπαρασκευή , commonly known by its Latin title Praeparatio evangelica, was a work of Christian apologetics written by Eusebius in the early part of the fourth century AD...
, Eratosthenes
Eratosthenes
Eratosthenes of Cyrene was a Greek mathematician, poet, athlete, geographer, astronomer, and music theorist.He was the first person to use the word "geography" and invented the discipline of geography as we understand it...
found the distance to the sun to be "σταδιων μυριαδας τετρακοσιας και οκτωκισμυριας" (literally "of stadia myriad
Myriad
Myriad , "numberlesscountless, infinite", is a classical Greek word for the number 10,000. In modern English, the word refers to an unspecified large quantity.-History and usage:...
s 400 and 80000"). This has been translated either as 4,080,000 stadia
Stadion (unit of length)
The stadion, Latinized as stadium and anglicized as stade, is an ancient Greek unit of length. According to Herodotus, one stade is equal to 600 feet. However, there were several different lengths of “feet”, depending on the country of origin....
(1903 translation by Edwin Hamilton Gifford
Edwin Hamilton Gifford
Edwin Hamilton Gifford, DD was an eminent Anglican Priest and author in the second half of the 19th century.Edwin Gifford was educated at Shrewsbury and St John's College, Cambridge. He was ordained in 1845. He was Second Master at his old school then Head Master of King Edward's School,...
), or as 804,000,000 stadia (edition of Édouard des Places, dated 1974-1991). Using the Greek stadium of 185 to 190 meters, the former translation comes to a far too low 755,000 km whereas the second translation comes to 148.7 to 152.8 million km (accurate within 2%). Hipparchus
Hipparchus
Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour...
also gave an estimate of the distance of the Sun from the Earth, quoted by Pappus
Pappus
Pappus may refer to:*Pappus , a type of flower structure*Pappus of Alexandria, Greek mathematician**Pappus's hexagon theorem, often just called 'Pappus's theorem', a theorem named for Pappus of Alexandria...
as equal to 490 Earth radii. According to the conjectural reconstructions of Noel Swerdlow
Noel Swerdlow
Noel M. Swerdlow is a professor emeritus of history, astronomy and astrophysics at the University of Chicago. He is currently a visiting professor at the California Institute of Technology.-Career:...
and G. J. Toomer, this was derived from his assumption of a "least perceptible" solar parallax of 7 arc minutes.
A Chinese
China
Chinese civilization may refer to:* China for more general discussion of the country.* Chinese culture* Greater China, the transnational community of ethnic Chinese.* History of China* Sinosphere, the area historically affected by Chinese culture...
mathematical treatise, the Zhoubi suanjing (ca. 1st century BCE), shows how the distance to the sun can be computed geometrically, using the different lengths of the noontime shadows observed at three places 1000 li apart and the assumption that the Earth is flat.
| Solar parallax |
Earth radii |
|
|---|---|---|
| Aristarchus Aristarchus of Samos Aristarchus, or more correctly Aristarchos , was a Greek astronomer and mathematician, born on the island of Samos, in Greece. He presented the first known heliocentric model of the solar system, placing the Sun, not the Earth, at the center of the known universe... (3rd cent. BC) |
40″ | 10,000 |
| Hipparchus Hipparchus Hipparchus, the common Latinization of the Greek Hipparkhos, can mean:* Hipparchus, the ancient Greek astronomer** Hipparchic cycle, an astronomical cycle he created** Hipparchus , a lunar crater named in his honour... (2nd cent. BC) |
7′ | 490 |
| Ptolemy Ptolemy Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the... (2nd cent.) |
2′ 50″ | 1,210 |
| Godefroy Wendelin Godefroy Wendelin Govaert Wendelen was a Flemish astronomer who was born in Herk-de-Stad. He is also known by the Latin name Vendelinus. His name is sometimes given as Godefroy Wendelin; his first name spelt Godefroid or Gottfried.Around 1630 he measured the distance between the Earth and the Sun using the method... (1635) |
15″ | 14,000 |
| Jeremiah Horrocks Jeremiah Horrocks Jeremiah Horrocks , sometimes given as Jeremiah Horrox , was an English astronomer who was the only person to predict, and one of only two people to observe and record, the transit of Venus of 1639.- Life and work :Horrocks was born in Lower Lodge, in... (1639) |
15″ | 14,000 |
| Christiaan Huygens (1659) | 8.6″ | 24,000 |
| Cassini Giovanni Domenico Cassini This article is about the Italian-born astronomer. For his French-born great-grandson, see Jean-Dominique Cassini.Giovanni Domenico Cassini was an Italian/French mathematician, astronomer, engineer, and astrologer... & Richer Jean Richer Jean Richer was a French astronomer and assistant of Giovanni Domenico Cassini.Between 1671 and 1673 he traveled to Cayenne at the request of the French Academy of Sciences to observe Mars during its perigee... (1672) |
9½″ | 21,700 |
| Jérôme Lalande Jérôme Lalande Joseph Jérôme Lefrançois de Lalande was a French astronomer and writer.-Biography:Lalande was born at Bourg-en-Bresse... (1771) |
8.6″ | 24,000 |
| Simon Newcomb Simon Newcomb Simon Newcomb was a Canadian-American astronomer and mathematician. Though he had little conventional schooling, he made important contributions to timekeeping as well as writing on economics and statistics and authoring a science fiction novel.-Early life:Simon Newcomb was born in the town of... (1895) |
8.80″ | 23,440 |
| Arthur Hinks Arthur Robert Hinks Arthur Robert Hinks, CBE, FRS was a British astronomer and geographer..As an astronomer, he is best known for his work in determining the distance from the Sun to the Earth from 1900–1909: for this achievement, he was awarded the Gold Medal of the Royal Astronomical Society and was elected a... (1909) |
8.807″ | 23,420 |
| H. Spencer Jones Harold Spencer Jones Sir Harold Spencer Jones KBE FRS was an English astronomer. Although born "Jones", his surname became "Spencer Jones".... (1941) |
8.790″ | 23,466 |
| modern | 8.794143″ | 23,455 |
In the 2nd century CE, Ptolemy
Ptolemy
Claudius Ptolemy , was a Roman citizen of Egypt who wrote in Greek. He was a mathematician, astronomer, geographer, astrologer, and poet of a single epigram in the Greek Anthology. He lived in Egypt under Roman rule, and is believed to have been born in the town of Ptolemais Hermiou in the...
estimated the mean distance of the sun as 1,210 times the Earth radius
Earth radius
Because the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
. To determine this value, Ptolemy started by measuring the Moon's parallax, finding what amounted to a horizontal lunar parallax of 1° 26′, which was much too large. He then derived a maximum lunar distance of 64 1/6 Earth radii. Because of cancelling errors in his parallax figure, his theory of the Moon's orbit, and other factors, this figure was approximately correct. He then measured the apparent sizes of the Sun and the Moon and concluded that the apparent diameter of the Sun was equal to the apparent diameter of the Moon at the Moon's greatest distance, and from records of lunar eclipses, he estimated this apparent diameter, as well as the apparent diameter of the shadow cone of the Earth traversed by the Moon during a lunar eclipse. Given these data, the distance of the Sun from the Earth can be trigonometrically computed to be 1,210 Earth radii. This gives a ratio of solar to lunar distance of approximately 19, matching Aristarchus's figure. Although Ptolemy's procedure is theoretically workable, it is very sensitive to small changes in the data, so much so that changing a measurement by a few percent can make the solar distance infinite.
After Greek astronomy was transmitted to the medieval Islamic world, astronomers made some changes to Ptolemy's cosmological model, but did not greatly change his estimate of the Earth-Sun distance. For example, in his introduction to Ptolemaic astronomy, al-Farghānī
Al-Farghani
' also known as Alfraganus in the West was a Persian astronomer and one of the famous astronomers in 9th century. The crater Alfraganus on the Moon is named after him.-Life:...
gave a mean solar distance of 1,170 Earth radii, while in his zij
Zij
Zīj is the generic name applied to Islamic astronomical books that tabulate parameters used for astronomical calculations of the positions of the Sun, Moon, stars, and planets. The name is derived from the Middle Persian term zih or zīg, meaning cord...
, al-Battānī
Al-Battani
Abū ʿAbd Allāh Muḥammad ibn Jābir ibn Sinān al-Raqqī al-Ḥarrānī al-Ṣābiʾ al-Battānī was a Muslim astronomer, astrologer, and mathematician...
used a mean solar distance of 1,108 Earth radii. Subsequent astronomers, such as al-Bīrūnī
Al-Biruni
Abū al-Rayḥān Muḥammad ibn Aḥmad al-BīrūnīArabic spelling. . The intermediate form Abū Rayḥān al-Bīrūnī is often used in academic literature...
, used similar values. Later in Europe, Copernicus
Nicolaus Copernicus
Nicolaus Copernicus was a Renaissance astronomer and the first person to formulate a comprehensive heliocentric cosmology which displaced the Earth from the center of the universe....
and Tycho Brahe
Tycho Brahe
Tycho Brahe , born Tyge Ottesen Brahe, was a Danish nobleman known for his accurate and comprehensive astronomical and planetary observations...
also used comparable figures (1,142 Earth radii and 1,150 Earth radii), and so Ptolemy's approximate Earth-Sun distance survived through the 16th century.
Johannes Kepler
Johannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
was the first to realize that Ptolemy's estimate must be significantly too low (according to Kepler, at least by a factor of three) in his Rudolphine Tables
Rudolphine Tables
The Rudolphine Tables consist of a star catalogue and planetary tables published by Johannes Kepler in 1627 using data from Tycho Brahe's observations.-Previous tables:...
(1627). Kepler's laws of planetary motion
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
allowed astronomers to calculate the relative distances of the planets from the Sun, and rekindled interest in measuring the absolute value for the Earth (which could then be applied to the other planets). The invention of the telescope
Telescope
A telescope is an instrument that aids in the observation of remote objects by collecting electromagnetic radiation . The first known practical telescopes were invented in the Netherlands at the beginning of the 1600s , using glass lenses...
allowed far more accurate measurements of angles than is possible with the naked eye. Flemish astronomer Godefroy Wendelin
Godefroy Wendelin
Govaert Wendelen was a Flemish astronomer who was born in Herk-de-Stad. He is also known by the Latin name Vendelinus. His name is sometimes given as Godefroy Wendelin; his first name spelt Godefroid or Gottfried.Around 1630 he measured the distance between the Earth and the Sun using the method...
repeated Aristarchus' measurements in 1635, and found that Ptolemy's value was too low by a factor of at least eleven.
A somewhat more accurate estimate can be obtained by observing the transit of Venus
Transit of Venus
A transit of Venus across the Sun takes place when the planet Venus passes directly between the Sun and Earth, becoming visible against the solar disk. During a transit, Venus can be seen from Earth as a small black disk moving across the face of the Sun...
. By measuring the transit in two different locations, one can accurately calculate the parallax
Parallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines. The term is derived from the Greek παράλλαξις , meaning "alteration"...
of Venus and from the relative distance of the Earth and Venus from the Sun, the solar parallax α (which cannot be measured directly). Jeremiah Horrocks
Jeremiah Horrocks
Jeremiah Horrocks , sometimes given as Jeremiah Horrox , was an English astronomer who was the only person to predict, and one of only two people to observe and record, the transit of Venus of 1639.- Life and work :Horrocks was born in Lower Lodge, in...
had attempted to produce an estimate based on his observation of the 1639 transit (published in 1662), giving a solar parallax of 15 arcseconds, similar to Wendelin's figure. The solar parallax is related to the Earth–Sun distance as measured in Earth radii
Earth radius
Because the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
by
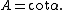
The smaller the solar parallax, the greater the distance between the Sun and the Earth: a solar parallax of 15" is equivalent to an Earth–Sun distance of 13,750 Earth radii.
Christiaan Huygens believed the distance was even greater: by comparing the apparent sizes of Venus and Mars
Mars
Mars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
, he estimated a value of about 24,000 Earth radii, equivalent to a solar parallax of 8.6". Although Huygens' estimate is remarkably close to modern values, it is often discounted by historians of astronomy because of the many unproven (and incorrect) assumptions he had to make for his method to work; the accuracy of his value seems to based more on luck than good measurement, with his various errors cancelling each other out.

Jean Richer
Jean Richer was a French astronomer and assistant of Giovanni Domenico Cassini.Between 1671 and 1673 he traveled to Cayenne at the request of the French Academy of Sciences to observe Mars during its perigee...
and Giovanni Domenico Cassini
Giovanni Domenico Cassini
This article is about the Italian-born astronomer. For his French-born great-grandson, see Jean-Dominique Cassini.Giovanni Domenico Cassini was an Italian/French mathematician, astronomer, engineer, and astrologer...
measured the parallax of Mars between Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
and Cayenne
Cayenne
Cayenne is the capital of French Guiana, an overseas region and department of France located in South America. The city stands on a former island at the mouth of the Cayenne River on the Atlantic coast. The city's motto is "Ferit Aurum Industria" which means "Work brings wealth"...
in French Guiana
French Guiana
French Guiana is an overseas region of France, consisting of a single overseas department located on the northern Atlantic coast of South America. It has borders with two nations, Brazil to the east and south, and Suriname to the west...
when Mars was at its closest to Earth in 1672. They arrived at a figure for the solar parallax of 9½", equivalent to an Earth–Sun distance of about 22,000 Earth radii. They were also the first astronomers to have access to an accurate and reliable value for the radius of the Earth, which had been measured by their colleague Jean Picard
Jean Picard
Jean-Felix Picard was a French astronomer and priest born in La Flèche, where he studied at the Jesuit Collège Royal Henry-Le-Grand. He was the first person to measure the size of the Earth to a reasonable degree of accuracy in a survey conducted in 1669–70, for which he is honored with a...
in 1669 as 3,269 thousand toise
Toise
A toise is a unit of measure for length, area and volume originating in pre-revolutionary France. In North America, it was used in colonial French establishments in early New France, French Louisiana , and Quebec...
s. Another colleague, Ole Rømer, discovered the finite speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in 1676: the speed was so great that it was usually quoted as the time required for light to travel from the Sun to the Earth, or "light time per unit distance", a convention that is still followed by astronomers today.
A better method for observing Venus transits was devised by James Gregory
James Gregory (astronomer and mathematician)
James Gregory FRS was a Scottish mathematician and astronomer. He described an early practical design for the reflecting telescope – the Gregorian telescope – and made advances in trigonometry, discovering infinite series representations for several trigonometric functions.- Biography :The...
and published in his Optica Promata (1663). It was strongly advocated by Edmond Halley
Edmond Halley
Edmond Halley FRS was an English astronomer, geophysicist, mathematician, meteorologist, and physicist who is best known for computing the orbit of the eponymous Halley's Comet. He was the second Astronomer Royal in Britain, following in the footsteps of John Flamsteed.-Biography and career:Halley...
and was applied to the transits of Venus observed in 1761 and 1769, and then again in 1874 and 1882. Transits of Venus occur in pairs, but less than one pair every century, and observing the transits in 1761 and 1769 was an unprecedented international scientific operation. Despite the Seven Years' War
Seven Years' War
The Seven Years' War was a global military war between 1756 and 1763, involving most of the great powers of the time and affecting Europe, North America, Central America, the West African coast, India, and the Philippines...
, dozens of astronomers were dispatched to observing points around the world at great expense and personal danger: several of them died in the endeavour. The various results were collated by Jérôme Lalande
Jérôme Lalande
Joseph Jérôme Lefrançois de Lalande was a French astronomer and writer.-Biography:Lalande was born at Bourg-en-Bresse...
to give a figure for the solar parallax of 8.6″.
| Date | Method | A/Gm | Uncertainty |
|---|---|---|---|
| 1895 | aberration | 149.25 | 0.12 |
| 1941 | parallax | 149.674 | 0.016 |
| 1964 | radar | 149.5981 | 0.001 |
| 1976 | telemetry | 149.597 870 | 0.000 001 |
| 2009 | telemetry | 149.597 870 700 | 0.000 000 003 |
Another method involved determining the constant of aberration
Aberration of light
The aberration of light is an astronomical phenomenon which produces an apparent motion of celestial objects about their real locations...
, and Simon Newcomb
Simon Newcomb
Simon Newcomb was a Canadian-American astronomer and mathematician. Though he had little conventional schooling, he made important contributions to timekeeping as well as writing on economics and statistics and authoring a science fiction novel.-Early life:Simon Newcomb was born in the town of...
gave great weight to this method when deriving his widely accepted value of 8.80″ for the solar parallax (close to the modern value of 8.794143″), although Newcomb also used data from the transits of Venus. Newcomb also collaborated with A. A. Michelson
Albert Abraham Michelson
Albert Abraham Michelson was an American physicist known for his work on the measurement of the speed of light and especially for the Michelson-Morley experiment. In 1907 he received the Nobel Prize in Physics...
to measure the speed of light with Earth-based equipment; combined with the constant of aberration (which is related to the light time per unit distance) this gave the first direct measurement of the Earth–Sun distance in kilometers. Newcomb's value for the solar parallax (and for the constant of aberration and the Gaussian gravitational constant
Gaussian gravitational constant
The Gaussian gravitational constant is an astronomical constant first proposed by German polymath Carl Friedrich Gauss in his 1809 work Theoria motus corporum coelestium in sectionibus conicis solem ambientum , although he had already used the concept to great success in predicting the...
) were incorporated into the first international system of astronomical constant
Astronomical constant
An astronomical constant is a physical constant used in astronomy. A formal set of constants, along with recommended values, was defined by the International Astronomical Union in 1976, and a new set of recommended values was produced in 1994...
s in 1896, which remained in place for the calculation of ephemerides
Ephemeris
An ephemeris is a table of values that gives the positions of astronomical objects in the sky at a given time or times. Different kinds of ephemerides are used for astronomy and astrology...
until 1964. The name "astronomical unit" appears first to have been used in 1903.
The discovery of the near-Earth asteroid 433 Eros
433 Eros
433 Eros is a near-Earth asteroid discovered in 1898, and the first asteroid to be orbited by a probe . It is an S-type asteroid approximately 34.4×11.2×11.2 km in size, the second-largest NEA after 1036 Ganymed, and belongs to the Amor group.Eros is a Mars-crosser asteroid, the first known...
and its passage near the Earth in 1900–1901 allowed a considerable improvement in parallax measurement. Another international project to measure the parallax of 433 Eros was undertaken in 1930–1931.
Direct radar measurements of the distances to Venus and Mars became available in the early 1960s. Along with improved measurements of the speed of light, these showed that Newcomb's values for the solar parallax and the constant of aberration were inconsistent with one another.
Developments
The unit distance A (the value of the astronomical unit in meters) can be expressed in terms of other astronomical constantAstronomical constant
An astronomical constant is a physical constant used in astronomy. A formal set of constants, along with recommended values, was defined by the International Astronomical Union in 1976, and a new set of recommended values was produced in 1994...
s:
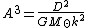
where G is the Newtonian gravitational constant, M☉ is the solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
, k is the Gaussian gravitational constant
Gaussian gravitational constant
The Gaussian gravitational constant is an astronomical constant first proposed by German polymath Carl Friedrich Gauss in his 1809 work Theoria motus corporum coelestium in sectionibus conicis solem ambientum , although he had already used the concept to great success in predicting the...
and D is the time period of one day.
The Sun is constantly losing mass by radiating away energy, so the orbits of the planets are steadily expanding outward from the Sun. This has led to calls to abandon the astronomical unit as a unit of measurement. There have also been calls to redefine the astronomical unit in terms of a fixed number of meters.
As the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
has an exact defined value in SI units and the Gaussian gravitational constant k is fixed in the astronomical system of units, measuring the light time per unit distance is exactly equivalent to measuring the product GM☉ in SI units. Hence, it is possible to construct ephemerides entirely in SI units, which is increasingly becoming the norm.
A 2004 analysis of radiometric measurements in the inner Solar System suggested that the secular increase
Secular variation
The secular variation of a time series is its long-term non-periodic variation . Whether something is perceived as a secular variation or not depends on the available timescale: a secular variation over a time scale of centuries may be part of a periodic variation over a time scale of millions of...
in the unit distance was much larger than can be accounted for by solar radiation, +15±4 meters per century.
Another explanation for the earth recession rate could be solar tidal friction. The moon's recession rate is governed by similar tidal friction with the earth. Takaho Miura of Hirosaki University in Japan suggested this possibility in 2009.
Later estimates based on both radiometric and angular observations lowered this estimate to +7±2 meters per century, but this is still far larger than can be accounted for by solar radiation and current theories of gravitation. The possible variation in the gravitational constant based on radiometric measurements is of the order of parts in 1012 per century, or lower. It has been suggested that the observed increase could be explained by the DGP model
DGP model
The DGP model is a model of gravity proposed by Gia Dvali, Gregory Gabadadze, and Massimo Porrati in 2000. The model is popular among some model builders, but has resisted being embedded into string theory....
.
Examples
The distances are approximate mean distances. It has to be taken into consideration that the distances between celestial bodiesAstronomical object
Astronomical objects or celestial objects are naturally occurring physical entities, associations or structures that current science has demonstrated to exist in the observable universe. The term astronomical object is sometimes used interchangeably with astronomical body...
change in time
Time
Time is a part of the measuring system used to sequence events, to compare the durations of events and the intervals between them, and to quantify rates of change such as the motions of objects....
due to their orbit
Orbit
In physics, an orbit is the gravitationally curved path of an object around a point in space, for example the orbit of a planet around the center of a star system, such as the Solar System...
s and other factors.
- The MoonMoonThe Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
is 0.0026 ± 0.0001 AU from the Earth - The EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
is 1.00 ± 0.02 AU from the SunSunThe Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields... - MarsMarsMars is the fourth planet from the Sun in the Solar System. The planet is named after the Roman god of war, Mars. It is often described as the "Red Planet", as the iron oxide prevalent on its surface gives it a reddish appearance...
is 1.52 ± 0.14 AU from the Sun - JupiterJupiterJupiter is the fifth planet from the Sun and the largest planet within the Solar System. It is a gas giant with mass one-thousandth that of the Sun but is two and a half times the mass of all the other planets in our Solar System combined. Jupiter is classified as a gas giant along with Saturn,...
is 5.20 ± 0.05 AU from the Sun - 8.4–9.8 AU: The radius of VY Canis MajorisVY Canis MajorisVY Canis Majoris is the largest known star and also one of the most luminous. Located in the constellation Canis Major, it is a red hypergiant, between 1800 and 2100 solar radii, 8.4–9.8 astronomical units in radius, about 3.0 billion km or 1.9 billion miles in diameter, and about 1.5 kiloparsecs ...
, the largest known star. - New HorizonsNew HorizonsNew Horizons is a NASA robotic spacecraft mission currently en route to the dwarf planet Pluto. It is expected to be the first spacecraft to fly by and study Pluto and its moons, Charon, Nix, Hydra and S/2011 P 1. Its estimated arrival date at the Pluto-Charon system is July 14th, 2015...
is 21 AU from the sun as of August 2011 as it makes it way to Pluto for a flyby. - PlutoPlutoPluto, formal designation 134340 Pluto, is the second-most-massive known dwarf planet in the Solar System and the tenth-most-massive body observed directly orbiting the Sun...
is 39.5 ± 9.8 AU from the Sun - The Kuiper BeltKuiper beltThe Kuiper belt , sometimes called the Edgeworth–Kuiper belt, is a region of the Solar System beyond the planets extending from the orbit of Neptune to approximately 50 AU from the Sun. It is similar to the asteroid belt, although it is far larger—20 times as wide and 20 to 200 times as massive...
begins at roughly 30 AU - Beginning of Scattered disk at 45 AU (10 AU overlap with Kuiper Belt)
- Ending of Kuiper Belt at 50-55 AU
- 90377 Sedna90377 Sedna90377 Sedna is a trans-Neptunian object discovered in 2003, which was about three times as far from the Sun as Neptune. For most of its orbit it is even further from the Sun, with its aphelion estimated at 960 astronomical units , making it one of the most distant known objects in the Solar System...
's orbit ranges between 76 and 942 AU from the Sun; Sedna is currently about 88 AU from the Sun - 94 AU: Termination shock between Solar windSolar windThe solar wind is a stream of charged particles ejected from the upper atmosphere of the Sun. It mostly consists of electrons and protons with energies usually between 1.5 and 10 keV. The stream of particles varies in temperature and speed over time...
s/Interstellar windsStellar windA stellar wind is a flow of neutral or charged gas ejected from the upper atmosphere of a star. It is distinguished from the bipolar outflows characteristic of young stars by being less collimated, although stellar winds are not generally spherically symmetric.Different types of stars have...
/Interstellar mediumInterstellar mediumIn astronomy, the interstellar medium is the matter that exists in the space between the star systems in a galaxy. This matter includes gas in ionic, atomic, and molecular form, dust, and cosmic rays. It fills interstellar space and blends smoothly into the surrounding intergalactic space... - 96.7 AU: The distance of dwarf planet ErisEris (dwarf planet)Eris, formal designation 136199 Eris, is the most massive known dwarf planet in the Solar System and the ninth most massive body known to orbit the Sun directly...
from the sun, as of 2009. Eris and its moon are currently the most distant known objects in the Solar System apart from long-period comets and space probeSpace probeA robotic spacecraft is a spacecraft with no humans on board, that is usually under telerobotic control. A robotic spacecraft designed to make scientific research measurements is often called a space probe. Many space missions are more suited to telerobotic rather than crewed operation, due to...
s. - 100 AU: Heliosheath
- 118 AU: , Voyager 1Voyager 1The Voyager 1 spacecraft is a 722-kilogram space probe launched by NASA in 1977, to study the outer Solar System and eventually interstellar space. Operating for as of today , the spacecraft receives routine commands and transmits data back to the Deep Space Network. At a distance of as of...
is the furthest human-made object from the Sun: it is currently travelling at about 3½ AU/yr - 100-1000 AU: Mostly populated by objects from the Scattered DiscScattered discThe scattered disc is a distant region of the Solar System that is sparsely populated by icy minor planets, a subset of the broader family of trans-Neptunian objects. The scattered-disc objects have orbital eccentricities ranging as high as 0.8, inclinations as high as 40°, and perihelia greater...
- 1000-3000 AU: Beginning of Hills cloud/"Inner Oort CloudOort cloudThe Oort cloud , or the Öpik–Oort cloud , is a hypothesized spherical cloud of comets which may lie roughly 50,000 AU, or nearly a light-year, from the Sun. This places the cloud at nearly a quarter of the distance to Proxima Centauri, the nearest star to the Sun...
" - 20,000 AU: Ending of Hills Cloud/"Inner Oort Cloud", beginning of "Outer Oort Cloud"
- 50,000 AU: possible closest estimate of the "Outer Oort Cloud" limits (0.8 lyLight-yearA light-year, also light year or lightyear is a unit of length, equal to just under 10 trillion kilometres...
) - 100,000 AU: possible farthest estimate of the "Outer Oort Cloud" limits (1.6 ly)
- 230,000 AU: maximum extent of influence of the Sun's gravitational fieldGravitational fieldThe gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
(Hill/Roche sphereHill sphereAn astronomical body's Hill sphere is the region in which it dominates the attraction of satellites. To be retained by a planet, a moon must have an orbit that lies within the planet's Hill sphere. That moon would, in turn, have a Hill sphere of its own...
)--beyond this is true interstellar mediumInterstellar mediumIn astronomy, the interstellar medium is the matter that exists in the space between the star systems in a galaxy. This matter includes gas in ionic, atomic, and molecular form, dust, and cosmic rays. It fills interstellar space and blends smoothly into the surrounding intergalactic space...
. This distance is 1.1 pc. - Proxima CentauriProxima CentauriProxima Centauri is a red dwarf star about 4.2 light-years distant in the constellation of Centaurus. It was discovered in 1915 by Robert Innes, the Director of the Union Observatory in South Africa, and is the nearest known star to the Sun, although it is too faint to be seen with the naked eye...
(the nearest starStarA star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
to EarthEarthEarth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
, excluding our own Sun) is ~268 000 AU from the Sun - The mean diameter of BetelgeuseBetelgeuseBetelgeuse, also known by its Bayer designation Alpha Orionis , is the eighth brightest star in the night sky and second brightest star in the constellation of Orion, outshining its neighbour Rigel only rarely...
is 5.5 AU (822 800 000 km) - The distance from the Sun to the centerGalactic CenterThe Galactic Center is the rotational center of the Milky Way galaxy. It is located at a distance of 8.33±0.35 kpc from the Earth in the direction of the constellations Sagittarius, Ophiuchus, and Scorpius where the Milky Way appears brightest...
of the Milky WayMilky WayThe Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
is approximately 1.7 AU
Conversion factors
- 1 AU = 149,597,870.700 ± 0.003 km ≈ 92,955,807.273 ± 0.002 mi ≈ 8.317 light minutesLight-yearA light-year, also light year or lightyear is a unit of length, equal to just under 10 trillion kilometres...
≈ 499 light-secondLight-secondA light-second is a unit of length useful in astronomy, telecommunications and relativistic physics. It is defined as the distance that light travels in free space in one second, and is equal to exactly 299,792,458 metres...
s - 1 light-secondLight-secondA light-second is a unit of length useful in astronomy, telecommunications and relativistic physics. It is defined as the distance that light travels in free space in one second, and is equal to exactly 299,792,458 metres...
≈ 0.002 AU - 1 gigameter ≈ 0.0067 AU
- 1 light-yearLight-yearA light-year, also light year or lightyear is a unit of length, equal to just under 10 trillion kilometres...
≈ 63,241 AU - 1 parsecParsecThe parsec is a unit of length used in astronomy. It is about 3.26 light-years, or just under 31 trillion kilometres ....
= 648,000/π ≈ 206,264.8 AU
External links
- The IAU and astronomical units
- Recommendations concerning Units (HTML version of the IAU Style Manual)
- Chasing Venus, Observing the Transits of Venus
- Transit of Venus

