
Gaussian gravitational constant
Encyclopedia

Astronomical constant
An astronomical constant is a physical constant used in astronomy. A formal set of constants, along with recommended values, was defined by the International Astronomical Union in 1976, and a new set of recommended values was produced in 1994...
first proposed by German polymath Carl Friedrich Gauss
Carl Friedrich Gauss
Johann Carl Friedrich Gauss was a German mathematician and scientist who contributed significantly to many fields, including number theory, statistics, analysis, differential geometry, geodesy, geophysics, electrostatics, astronomy and optics.Sometimes referred to as the Princeps mathematicorum...
in his 1809 work Theoria motus corporum coelestium in sectionibus conicis solem ambientum ("Theory of Motion of the Celestial Bodies Moving in Conic Sections around the Sun"), although he had already used the concept to great success in predicting the orbit of Ceres in 1801. It is equal to the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of GM where G is the Newtonian gravitational constant and M is the solar mass and roughly equal to the mean angular velocity
Angular velocity
In physics, the angular velocity is a vector quantity which specifies the angular speed of an object and the axis about which the object is rotating. The SI unit of angular velocity is radians per second, although it may be measured in other units such as degrees per second, revolutions per...
of the Earth in orbit around the Sun. The Gaussian gravitational constant is related to an expression which is the same for all bodies orbiting the Sun. A different constant is needed for the objects in orbit about another body.
Its value was measured to great precision by Canadian-American astronomer Simon Newcomb
Simon Newcomb
Simon Newcomb was a Canadian-American astronomer and mathematician. Though he had little conventional schooling, he made important contributions to timekeeping as well as writing on economics and statistics and authoring a science fiction novel.-Early life:Simon Newcomb was born in the town of...
in his Tables of the Sun
Newcomb's Tables of the Sun
Newcomb's Tables of the Sun is the short title and running head of a work by the American astronomer and mathematician Simon Newcomb entitled "Tables of the Motion of the Earth on its Axis and Around the Sun" on pages 1–169 of "Tables of the Four Inner Planets" , volume VI of the serial publication...
(1895): his numerical value of in the astronomical system of units is the value that was calculated by Gauss and still used today. It formed the basis of the definition of the international second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
from 1956 to 1967, and has been a defining constant in the astronomical system of units since 1952.
Derivation
In Theoria Motus Gauss gave an expression for all bodies orbiting the Sun that had a constant value. To derive this expression we need the specific relative angular momentumSpecific relative angular momentum
The specific relative angular momentum is also known as the areal momentum .In astrodynamics, the specific relative angular momentum of two orbiting bodies is the vector product of the relative position and the relative velocity. Equivalently, it is the total angular momentum divided by the...
, h, which is related to the areal velocity
Areal velocity
Areal velocity is the rate at which area is swept out by a particle as it moves along a curve. In many applications, the curve lies in a plane, but in others, it is a space curve....
and a constant of the motion of a planet and the formulae for free orbits. We note that h is equal to the area, ΔA, swept out by the radius divided by the time, Δt, and also related to the parameter, p = h2/μ, so,
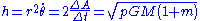
On dividing by the variable quantities on the right associated with the orbiting body we get,
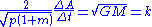
For a 1AU circular orbit p = 1AU, the area bounded by the orbit is ΔA = π AU2 and Gauss sets Δt = 365.2563835, the sidereal period, and the mass of the Earth, m, equal to 1/354710 solar masses which yields k = 0.01720209895. Gauss used relative values for his measurements so his value for k is unitless and measured in radians. If we treat mass and distance as relative measurements and use the day as the unit of time then the units for k are radians per day. The Gaussian gravitational constant is now used to define the astronomical unit
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
.
Gauss' constant can be used as the constant of proportionality in the formula for the mean daily motion
Mean motion
Mean motion, n\,\!, is a measure of how fast a satellite progresses around its elliptical orbit. Unless the orbit is circular, the mean motion is only an average value, and does not represent the instantaneous angular rate....
, n (in radians per day), for bodies in elliptical orbits. The mean motion is a simple function the semi-major axis, a, in AU.

In General Relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
this formula is sometimes written as ω2a3 = M. In the case of nearly circular planetary orbits about the Sun one can show in General Relativity that the equation for the orbit is approximately the same as the classical orbit with the exception that the plane of the orbit precesses slowly about the Sun resulting in an advance in perihelion. To first approximation we still have the parameter p = h2/μ. So the derivation of the constant function above is also valid in General Relativity to the order of the approximation but we have to use the precessing orbital plane and its slightly decreased mean motion to determine the perihelion period.
The term "gravitational constant" comes from the fact that k2 is related to the standard gravitational parameter expressed in a system of measurement where masses are measured in solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
es, time is measured in days and distance is measured in semi-major axes of the Earth's orbit. By transforming the system of measurement, Gauss had been able to greatly simplify the calculation of planetary orbits. This basic system (slightly modified in the definitions of the base units) is still used today as the astronomical system of units.
Later definitions
Gauss was not fully aware of the secular increase in the length of the mean solar day and unaware of the relativistic differences in the rate of clocks. His original constant was not empirically measured for a full year.When Canadian-American astronomer Simon Newcomb
Simon Newcomb
Simon Newcomb was a Canadian-American astronomer and mathematician. Though he had little conventional schooling, he made important contributions to timekeeping as well as writing on economics and statistics and authoring a science fiction novel.-Early life:Simon Newcomb was born in the town of...
was appointed director of the Naval Almanac Office of the United States Naval Observatory
United States Naval Observatory
The United States Naval Observatory is one of the oldest scientific agencies in the United States, with a primary mission to produce Positioning, Navigation, and Timing for the U.S. Navy and the U.S. Department of Defense...
in 1877, he set about a program of redetermination of the astronomical constant
Astronomical constant
An astronomical constant is a physical constant used in astronomy. A formal set of constants, along with recommended values, was defined by the International Astronomical Union in 1976, and a new set of recommended values was produced in 1994...
s with George William Hill
George William Hill
George William Hill , was an American astronomer and mathematician.Hill was born in New York City, New York to painter and engraver John William Hill. and Catherine Smith Hill. He moved to West Nyack with his family when he was eight years old. After attending high school, Hill graduated from...
. Their efforts led to the preparation of Newcomb's Tables of the Sun
Newcomb's Tables of the Sun
Newcomb's Tables of the Sun is the short title and running head of a work by the American astronomer and mathematician Simon Newcomb entitled "Tables of the Motion of the Earth on its Axis and Around the Sun" on pages 1–169 of "Tables of the Four Inner Planets" , volume VI of the serial publication...
in 1895, which were based on a value of the Gaussian gravitation constant of , where A is the length of the semi-major axis of the Earth's orbit, S is the solar mass
Solar mass
The solar mass , , is a standard unit of mass in astronomy, used to indicate the masses of other stars and galaxies...
and D is the mean solar day
Solar time
Solar time is a reckoning of the passage of time based on the Sun's position in the sky. The fundamental unit of solar time is the day. Two types of solar time are apparent solar time and mean solar time .-Introduction:...
at J1900.0. In 1938, the International Astronomical Union
International Astronomical Union
The International Astronomical Union IAU is a collection of professional astronomers, at the Ph.D. level and beyond, active in professional research and education in astronomy...
(IAU) adopted the above value for all future ephemerides
Ephemeris
An ephemeris is a table of values that gives the positions of astronomical objects in the sky at a given time or times. Different kinds of ephemerides are used for astronomy and astrology...
.
When Ephemeris Time
Ephemeris time
The term ephemeris time can in principle refer to time in connection with any astronomical ephemeris. In practice it has been used more specifically to refer to:...
was adopted in 1952, the length of the ephemeris second
Second
The second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
was defined to be consistent with Newcomb's value of k, so the length of the ephemeris day was exactly 86400 ephemeris seconds. Although the definition of the ephemeris second (and later the international second in 1956 and the SI second in 1960) refers to a fixed fraction of the tropical year
Tropical year
A tropical year , for general purposes, is the length of time that the Sun takes to return to the same position in the cycle of seasons, as seen from Earth; for example, the time from vernal equinox to vernal equinox, or from summer solstice to summer solstice...
at J1900.0, the only measure of the tropical year at that epoch
Epoch (astronomy)
In astronomy, an epoch is a moment in time used as a reference point for some time-varying astronomical quantity, such as celestial coordinates, or elliptical orbital elements of a celestial body, where these are subject to perturbations and vary with time...
was Newcomb's Tables, based on his measured value of the Gaussian gravitational constant. In effect, the second was redefined to better agree with Newcomb's Tables and hence with his value for k.
Newcomb was aware of the secular variation in the length of the mean solar day caused by tidal acceleration
Tidal acceleration
Tidal acceleration is an effect of the tidal forces between an orbiting natural satellite , and the primary planet that it orbits . The "acceleration" is usually negative, as it causes a gradual slowing and recession of a satellite in a prograde orbit away from the primary, and a corresponding...
, but he does not appear to have fully corrected for it. By extrapolating from modern measurements, the date on which the mean solar day would have been exactly 86400 seconds long was about 1820, neatly in the middle of the data (from 1750–1890) which Newcomb used to prepare his Tables.
The astronomical system of units was redefined in 1976 to fix the value of k at precisely . The value of the astronomical unit
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
is no longer defined as the semi-major axis of the Earth's orbit, but instead is that length which give exactly Newcomb's 1895 value of the Gaussian gravitational constant. In modern ephemerides, the mean orbital axis of the Earth is slightly longer than 1 AU, and the sidereal year
Sidereal year
A sidereal year is the time taken by the Earth to orbit the Sun once with respect to the fixed stars. Hence it is also the time taken for the Sun to return to the same position with respect to the fixed stars after apparently travelling once around the ecliptic. It was equal to at noon 1 January...
is slightly shorter than 1 Gaussian year
Gaussian year
A Gaussian year is defined as 365.2568983 days. It was adopted by Carl Friedrich Gauss as the length of the sidereal year in his studies of the dynamics of the solar system.A slightly different value is now accepted as the length of the sidereal year,...
. The day was also redefined to be exactly 86400 SI seconds when measured at mean sea level on the Earth: in practice, it is measured in Barycentric Dynamical Time
Barycentric Dynamical Time
Barycentric Dynamical Time is a relativistic coordinate time scale, intended for astronomical use as a time standard to take account of time dilation when calculating orbits and astronomical ephemerides of planets, asteroids, comets and interplanetary spacecraft in the Solar system...
(TDB).

