Linear
Encyclopedia
In mathematics
, a linear map or function
f(x) is a function which satisfies the following two properties:
It can be shown that additivity implies the homogeneity in all cases where α is rational
; this is done by proving the case where α is a natural number by mathematical induction
and then extending the result to arbitrary rational numbers. If f is assumed to be continuous as well then this can be extended to show that homogeneity for α any real number, using the fact that rationals form a dense subset of the reals.
In this definition, x is not necessarily a real number
, but can in general be a member of any vector space
. A less restrictive definition
of linear function, not coinciding with the definition of linear map, is used in elementary mathematics.
The concept of linearity can be extended to linear operators. Important examples of linear operators include the derivative
considered as a differential operator
, and many constructed from it, such as del
and the Laplacian. When a differential equation
can be expressed in linear form, it is particularly easy to solve by breaking the equation up into smaller pieces, solving each of those pieces, and adding the solutions up.
Linear algebra
is the branch of mathematics concerned with the study of vectors, vector spaces (also called linear spaces), linear transformations (also called linear maps), and systems of linear equations.
The word linear comes from the Latin
word linearis, which means pertaining to or resembling a line. For a description of linear and nonlinear equations, see linear equation
. Nonlinear equations and functions are of interest to physicist
s and mathematician
s because they can be used to represent many natural phenomena, including chaos
.
, or in ppm (parts per million) of full scale. Typically, the straight line is obtained by performing a least-squares fit of the data. The three definitions vary in the
manner in which the straight line is positioned relative to the actual device's performance. Also, all three of these definitions ignore any gain, or offset errors that may be present in the actual device's performance characteristics.
Many times a device's specifications will simply refer to linearity, with no other explanation as to which type of linearity is intended. In cases where a specification is expressed simply as linearity, it is assumed to imply independent linearity.
Independent linearity is probably the most commonly-used linearity definition and is often found in the specifications for DMM
s and ADC
s, as well as devices like potentiometer
s. Independent linearity is defined as the maximum deviation of actual performance relative to a straight line, located such that it minimizes the maximum deviation. In that case there are no constraints placed upon the positioning of the straight line and it may be wherever necessary to minimize the deviations between it and the device's actual performance characteristic.
Zero-based linearity forces the lower range value of the straight line to be equal to the actual lower range value of the device's characteristic, but it does allow the line to be rotated to minimize the maximum deviation. In this case, since the positioning of the straight line is constrained by the requirement that the lower range values of the line and the device's characteristic be coincident, the non-linearity based on this definition will generally be larger than for independent linearity.
For terminal linearity, there is no flexibility allowed in the placement of the straight line in order to minimize the deviations. The straight line must be located such that each of its end-points coincides with the device's actual upper and lower range values. This means that the non-linearity measured by this definition will typically be larger than that measured by the independent, or the zero-based linearity definitions. This definition of linearity is often associated with ADCs, DAC
s and various sensors.
A fourth linearity definition, absolute linearity, is sometimes also encountered. Absolute linearity is a variation of terminal linearity, in that it allows no flexibility in the placement of the straight line, however in this case the gain and offset errors of the actual device are included in the linearity measurement, making this the most difficult measure of a device's performance. For absolute linearity the end points of the straight line are defined by the ideal upper and lower range values for the device, rather than the actual values. The linearity error in this instance is the maximum deviation of the actual device's performance from ideal.
of degree
1 is said to be linear, because the graph of a function
of that form is a line
.
Over the reals, a linear equation
is one of the forms:
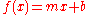
where m is often called the slope
or gradient
; b the y-intercept
, which gives the point of intersection between the graph of the function and the y-axis.
Note that this usage of the term linear is not the same as the above, because linear polynomials over the real numbers do not in general satisfy either additivity or homogeneity. In fact, they do so if and only if
b = 0. Hence, if b ≠ 0, the function is often called an affine function (see in greater generality affine transformation
).
for which there exist 
such that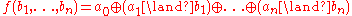
for all 
A Boolean function is linear if one of the following holds for the function's truth table
:
Another way to express this is that each variable always makes a difference in the truth-value of the operation or it never makes a difference.
Negation
, Logical biconditional
, exclusive or, tautology
, and contradiction
are linear functions.
, linearity is a property of the differential equations governing many systems; for instance, the Maxwell equations or the diffusion equation.
Linearity of a differential equation
means that if two functions f and g are solutions of the equation, then their sum f+g is too.
, the linear operating region of a device, for example a transistor
, is where a dependent variable (such as the transistor collector current
) is directly proportional
to an independent variable
(such as the base current). This ensures that an analog output is an accurate representation of an input, typically with higher amplitude (amplified). A typical example of linear equipment is a high fidelity
audio amplifier
, which must amplify a signal without changing its waveform. Others are linear filter
s, linear regulator
s, and linear amplifier
s in general.
In most scientific
and technological
, as distinct from mathematical, applications, something may be described as linear if the characteristic is approximately but not exactly a straight line; and linearity may be valid only within a certain operating region—for example, a high-fidelity amplifier may distort even a small signal, but sufficiently little to be acceptable (acceptable but imperfect linearity); and may distort very badly if the input exceeds a certain value, taking it away from the approximately linear part of the transfer function
.
protected by handgunners towards shallow formations of handgunners protected by progressively fewer pikes. This kind of formation would get thinner until its extreme in the age of Wellington with the 'Thin Red Line
'. It would eventually be replaced by skirmish order at the time of the invention of the breech-loading rifle that allowed soldiers to move and fire independently of the large scale formations and fight in small, mobile units.
to distinguish "Classic", or Renaissance art, from the Baroque
. According to Wölfflin, painters of the fifteenth and early sixteenth centuries (Leonardo da Vinci
, Raphael
or Albrecht Dürer
) are more linear than "painterly
" Baroque painters of the seventeenth century (Peter Paul Rubens, Rembrandt, and Velázquez
) because they primarily use outline to create shape
. Linearity in art can also be referenced in digital art
. For example, hypertext fiction
can be an example of nonlinear narrative, but there are also websites designed to go in a specified, organized manner, following a linear path.
s or melody, as opposed to simultaneity
or the vertical
aspect.
both descend from the same root meaning, the Latin
word for line, which is "linea".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a linear map or function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f(x) is a function which satisfies the following two properties:
- AdditivityAdditive functionIn mathematics the term additive function has two different definitions, depending on the specific field of application.In algebra an additive function is a function that preserves the addition operation:for any two elements x and y in the domain. For example, any linear map is additive...
(also called the superposition propertySuperposition principleIn physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
): f(x + y) = f(x) + f(y). This says that f is a group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
with respect to addition. - HomogeneityHomogeneous functionIn mathematics, a homogeneous function is a function with multiplicative scaling behaviour: if the argument is multiplied by a factor, then the result is multiplied by some power of this factor. More precisely, if is a function between two vector spaces over a field F, and k is an integer, then...
of degree 1: f(αx) = αf(x) for all α.
It can be shown that additivity implies the homogeneity in all cases where α is rational
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
; this is done by proving the case where α is a natural number by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
and then extending the result to arbitrary rational numbers. If f is assumed to be continuous as well then this can be extended to show that homogeneity for α any real number, using the fact that rationals form a dense subset of the reals.
In this definition, x is not necessarily a real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, but can in general be a member of any vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. A less restrictive definition
Linear function
In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....
of linear function, not coinciding with the definition of linear map, is used in elementary mathematics.
The concept of linearity can be extended to linear operators. Important examples of linear operators include the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
considered as a differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
, and many constructed from it, such as del
Del
In vector calculus, del is a vector differential operator, usually represented by the nabla symbol \nabla . When applied to a function defined on a one-dimensional domain, it denotes its standard derivative as defined in calculus...
and the Laplacian. When a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
can be expressed in linear form, it is particularly easy to solve by breaking the equation up into smaller pieces, solving each of those pieces, and adding the solutions up.
Linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
is the branch of mathematics concerned with the study of vectors, vector spaces (also called linear spaces), linear transformations (also called linear maps), and systems of linear equations.
The word linear comes from the Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
word linearis, which means pertaining to or resembling a line. For a description of linear and nonlinear equations, see linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
. Nonlinear equations and functions are of interest to physicist
Physicist
A physicist is a scientist who studies or practices physics. Physicists study a wide range of physical phenomena in many branches of physics spanning all length scales: from sub-atomic particles of which all ordinary matter is made to the behavior of the material Universe as a whole...
s and mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
s because they can be used to represent many natural phenomena, including chaos
Chaos theory
Chaos theory is a field of study in mathematics, with applications in several disciplines including physics, economics, biology, and philosophy. Chaos theory studies the behavior of dynamical systems that are highly sensitive to initial conditions, an effect which is popularly referred to as the...
.
Integral linearity
For a device that converts a quantity to another quantity there are three basic definitions for integral linearity in common use: independent linearity, zero-based linearity, and terminal, or end-point, linearity. In each case, linearity defines how well the device's actual performance across a specified operating range approximates a straight line. Linearity is usually measured in terms of a deviation, or non-linearity, from an ideal straight line and it is typically expressed in terms of percent of full scaleFull scale
In electronics and signal processing, full scale or full code represents the maximum amplitude a system can present.-Electronics and signal processing:...
, or in ppm (parts per million) of full scale. Typically, the straight line is obtained by performing a least-squares fit of the data. The three definitions vary in the
THE
THE is a three-letter acronym that may refer to:*Technische Hogeschool Eindhoven , a Dutch university of technology...
manner in which the straight line is positioned relative to the actual device's performance. Also, all three of these definitions ignore any gain, or offset errors that may be present in the actual device's performance characteristics.
Many times a device's specifications will simply refer to linearity, with no other explanation as to which type of linearity is intended. In cases where a specification is expressed simply as linearity, it is assumed to imply independent linearity.
Independent linearity is probably the most commonly-used linearity definition and is often found in the specifications for DMM
Multimeter
A multimeter or a multitester, also known as a VOM , is an electronic measuring instrument that combines several measurement functions in one unit. A typical multimeter may include features such as the ability to measure voltage, current and resistance...
s and ADC
Analog-to-digital converter
An analog-to-digital converter is a device that converts a continuous quantity to a discrete time digital representation. An ADC may also provide an isolated measurement...
s, as well as devices like potentiometer
Potentiometer
A potentiometer , informally, a pot, is a three-terminal resistor with a sliding contact that forms an adjustable voltage divider. If only two terminals are used , it acts as a variable resistor or rheostat. Potentiometers are commonly used to control electrical devices such as volume controls on...
s. Independent linearity is defined as the maximum deviation of actual performance relative to a straight line, located such that it minimizes the maximum deviation. In that case there are no constraints placed upon the positioning of the straight line and it may be wherever necessary to minimize the deviations between it and the device's actual performance characteristic.
Zero-based linearity forces the lower range value of the straight line to be equal to the actual lower range value of the device's characteristic, but it does allow the line to be rotated to minimize the maximum deviation. In this case, since the positioning of the straight line is constrained by the requirement that the lower range values of the line and the device's characteristic be coincident, the non-linearity based on this definition will generally be larger than for independent linearity.
For terminal linearity, there is no flexibility allowed in the placement of the straight line in order to minimize the deviations. The straight line must be located such that each of its end-points coincides with the device's actual upper and lower range values. This means that the non-linearity measured by this definition will typically be larger than that measured by the independent, or the zero-based linearity definitions. This definition of linearity is often associated with ADCs, DAC
Digital-to-analog converter
In electronics, a digital-to-analog converter is a device that converts a digital code to an analog signal . An analog-to-digital converter performs the reverse operation...
s and various sensors.
A fourth linearity definition, absolute linearity, is sometimes also encountered. Absolute linearity is a variation of terminal linearity, in that it allows no flexibility in the placement of the straight line, however in this case the gain and offset errors of the actual device are included in the linearity measurement, making this the most difficult measure of a device's performance. For absolute linearity the end points of the straight line are defined by the ideal upper and lower range values for the device, rather than the actual values. The linearity error in this instance is the maximum deviation of the actual device's performance from ideal.
Linear polynomials
In a different usage to the above, a polynomialPolynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
of degree
Degree (mathematics)
In mathematics, there are several meanings of degree depending on the subject.- Unit of angle :A degree , usually denoted by ° , is a measurement of a plane angle, representing 1⁄360 of a turn...
1 is said to be linear, because the graph of a function
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
of that form is a line
Line (geometry)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
.
Over the reals, a linear equation
Linear equation
A linear equation is an algebraic equation in which each term is either a constant or the product of a constant and a single variable....
is one of the forms:
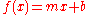
where m is often called the slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
or gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
; b the y-intercept
Y-intercept
In coordinate geometry, using the common convention that the horizontal axis represents a variable x and the vertical axis represents a variable y, a y-intercept is a point where the graph of a function or relation intersects with the y-axis of the coordinate system...
, which gives the point of intersection between the graph of the function and the y-axis.
Note that this usage of the term linear is not the same as the above, because linear polynomials over the real numbers do not in general satisfy either additivity or homogeneity. In fact, they do so if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
b = 0. Hence, if b ≠ 0, the function is often called an affine function (see in greater generality affine transformation
Affine transformation
In geometry, an affine transformation or affine map or an affinity is a transformation which preserves straight lines. It is the most general class of transformations with this property...
).
Boolean functions
In Boolean algebra, a linear function is a function for which there exist such that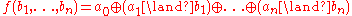 for all A Boolean function is linear if one of the following holds for the function's truth table
Truth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra, boolean functions, and propositional calculus—to compute the functional values of logical expressions on each of their functional arguments, that is, on each combination of values taken by their...
:
- In every row in which the truth value of the function is 'T', there are an odd number of 'T's assigned to the arguments and in every row in which the function is 'F' there is an even number of 'T's assigned to arguments. Specifically, f('F', 'F', ..., 'F') = 'F', and these functions correspond to linear maps over the Boolean vector space.
- In every row in which the value of the function is 'T', there is an even number of 'T's assigned to the arguments of the function; and in every row in which the truth value of the function is 'F', there are an odd number of 'T's assigned to arguments. In this case, f('F', 'F', ..., 'F') = 'T'.
Another way to express this is that each variable always makes a difference in the truth-value of the operation or it never makes a difference.
Negation
Negation
In logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
, Logical biconditional
Logical biconditional
In logic and mathematics, the logical biconditional is the logical connective of two statements asserting "p if and only if q", where q is a hypothesis and p is a conclusion...
, exclusive or, tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
, and contradiction
Contradiction
In classical logic, a contradiction consists of a logical incompatibility between two or more propositions. It occurs when the propositions, taken together, yield two conclusions which form the logical, usually opposite inversions of each other...
are linear functions.
Physics
In physicsPhysics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, linearity is a property of the differential equations governing many systems; for instance, the Maxwell equations or the diffusion equation.
Linearity of a differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
means that if two functions f and g are solutions of the equation, then their sum f+g is too.
Electronics
In electronicsElectronics
Electronics is the branch of science, engineering and technology that deals with electrical circuits involving active electrical components such as vacuum tubes, transistors, diodes and integrated circuits, and associated passive interconnection technologies...
, the linear operating region of a device, for example a transistor
Transistor
A transistor is a semiconductor device used to amplify and switch electronic signals and power. It is composed of a semiconductor material with at least three terminals for connection to an external circuit. A voltage or current applied to one pair of the transistor's terminals changes the current...
, is where a dependent variable (such as the transistor collector current
Electric current
Electric current is a flow of electric charge through a medium.This charge is typically carried by moving electrons in a conductor such as wire...
) is directly proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
to an independent variable
Independent variable
The terms "dependent variable" and "independent variable" are used in similar but subtly different ways in mathematics and statistics as part of the standard terminology in those subjects...
(such as the base current). This ensures that an analog output is an accurate representation of an input, typically with higher amplitude (amplified). A typical example of linear equipment is a high fidelity
High fidelity
High fidelity—or hi-fi—reproduction is a term used by home stereo listeners and home audio enthusiasts to refer to high-quality reproduction of sound or images, to distinguish it from the poorer quality sound produced by inexpensive audio equipment...
audio amplifier
Audio amplifier
An audio amplifier is an electronic amplifier that amplifies low-power audio signals to a level suitable for driving loudspeakers and is the final stage in a typical audio playback chain.The preceding stages in such a chain are low power audio amplifiers which perform tasks like pre-amplification,...
, which must amplify a signal without changing its waveform. Others are linear filter
Linear filter
Linear filters in the time domain process time-varying input signals to produce output signals, subject to the constraint of linearity.This results from systems composed solely of components classified as having a linear response....
s, linear regulator
Linear regulator
In electronics, a linear regulator is a voltage regulator based on an active device operating in its "linear region" or passive devices like Zener diodes operated in their breakdown region...
s, and linear amplifier
Linear amplifier
A linear amplifier is an electronic circuit whose output is proportional to its input, but capable of delivering more power into a load. The term usually refers to a type of radio-frequency power amplifier, some of which have output power measured in kilowatts, and are used in amateur radio...
s in general.
In most scientific
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
and technological
Technology
Technology is the making, usage, and knowledge of tools, machines, techniques, crafts, systems or methods of organization in order to solve a problem or perform a specific function. It can also refer to the collection of such tools, machinery, and procedures. The word technology comes ;...
, as distinct from mathematical, applications, something may be described as linear if the characteristic is approximately but not exactly a straight line; and linearity may be valid only within a certain operating region—for example, a high-fidelity amplifier may distort even a small signal, but sufficiently little to be acceptable (acceptable but imperfect linearity); and may distort very badly if the input exceeds a certain value, taking it away from the approximately linear part of the transfer function
Transfer function
A transfer function is a mathematical representation, in terms of spatial or temporal frequency, of the relation between the input and output of a linear time-invariant system. With optical imaging devices, for example, it is the Fourier transform of the point spread function i.e...
.
Military tactical formations
In military tactical formations, "linear formations" were adapted from phalanx-like formations of pikePike (weapon)
A pike is a pole weapon, a very long thrusting spear used extensively by infantry both for attacks on enemy foot soldiers and as a counter-measure against cavalry assaults. Unlike many similar weapons, the pike is not intended to be thrown. Pikes were used regularly in European warfare from the...
protected by handgunners towards shallow formations of handgunners protected by progressively fewer pikes. This kind of formation would get thinner until its extreme in the age of Wellington with the 'Thin Red Line
The Thin Red Line (1854 battle)
The Thin Red Line was a military action by the Sutherland Highlanders red-coated 93rd Regiment at the Battle of Balaclava on October 25, 1854, during the Crimean War. In this incident the 93rd aided by a small force of Royal Marines and some Turkish infantrymen, led by Sir Colin Campbell, routed a...
'. It would eventually be replaced by skirmish order at the time of the invention of the breech-loading rifle that allowed soldiers to move and fire independently of the large scale formations and fight in small, mobile units.
Art
Linear is one of the five categories proposed by Swiss art historian Heinrich WölfflinHeinrich Wölfflin
Heinrich Wölfflin was a famous Swiss art critic, whose objective classifying principles were influential in the development of formal analysis in the history of art during the 20th century. He taught at Basel, Berlin and Munich in the generation that raised German art history to pre-eminence...
to distinguish "Classic", or Renaissance art, from the Baroque
Baroque
The Baroque is a period and the style that used exaggerated motion and clear, easily interpreted detail to produce drama, tension, exuberance, and grandeur in sculpture, painting, literature, dance, and music...
. According to Wölfflin, painters of the fifteenth and early sixteenth centuries (Leonardo da Vinci
Leonardo da Vinci
Leonardo di ser Piero da Vinci was an Italian Renaissance polymath: painter, sculptor, architect, musician, scientist, mathematician, engineer, inventor, anatomist, geologist, cartographer, botanist and writer whose genius, perhaps more than that of any other figure, epitomized the Renaissance...
, Raphael
Raphael
Raffaello Sanzio da Urbino , better known simply as Raphael, was an Italian painter and architect of the High Renaissance. His work is admired for its clarity of form and ease of composition and for its visual achievement of the Neoplatonic ideal of human grandeur...
or Albrecht Dürer
Albrecht Dürer
Albrecht Dürer was a German painter, printmaker, engraver, mathematician, and theorist from Nuremberg. His prints established his reputation across Europe when he was still in his twenties, and he has been conventionally regarded as the greatest artist of the Northern Renaissance ever since...
) are more linear than "painterly
Painterly
Painterliness is a translation of the German term , a word popularized by Swiss art historian Heinrich Wölfflin in order to help focus, enrich and standardize the terms being used by art historians of his time to characterize works of art...
" Baroque painters of the seventeenth century (Peter Paul Rubens, Rembrandt, and Velázquez
Diego Velázquez
Diego Rodríguez de Silva y Velázquez was a Spanish painter who was the leading artist in the court of King Philip IV. He was an individualistic artist of the contemporary Baroque period, important as a portrait artist...
) because they primarily use outline to create shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
. Linearity in art can also be referenced in digital art
Digital art
Digital art is a general term for a range of artistic works and practices that use digital technology as an essential part of the creative and/or presentation process...
. For example, hypertext fiction
Hypertext fiction
Hypertext fiction is a genre of electronic literature, characterized by the use of hypertext links which provides a new context for non-linearity in "literature" and reader interaction. The reader typically chooses links to move from one node of text to the next, and in this fashion arranges a...
can be an example of nonlinear narrative, but there are also websites designed to go in a specified, organized manner, following a linear path.
Music
In music the linear aspect is succession, either intervalInterval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
s or melody, as opposed to simultaneity
Simultaneity (music)
In music, a simultaneity is more than one complete musical texture occurring at the same time, rather than in succession. This first appeared in the music of Charles Ives, and is common in the music of Conlon Nancarrow and others....
or the vertical
Interval (music)
In music theory, an interval is a combination of two notes, or the ratio between their frequencies. Two-note combinations are also called dyads...
aspect.
Measurement
In measurement, the term "linear foot" refers to the number of feet in a straight line of material (such as lumber or fabric) generally without regard to the width. It is sometimes incorrectly referred to as "lineal feet"; however, "lineal" is typically reserved for usage when referring to ancestry or heredity.http://www.unc.edu/~rowlett/units/dictL.html The words "linear"http://www.yourdictionary.com/ahd/l/l0180100.html & "lineal" http://www.yourdictionary.com/ahd/l/l0180300.htmlboth descend from the same root meaning, the Latin
Latin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
word for line, which is "linea".
See also
- Linear elementLinear elementIn an electric circuit, a linear element is an electrical element with a linear relationship between current and [output[voltage]]. Resistors are the most common example of a linear element; other examples include capacitors, inductors, and transformers....
- Linear systemLinear systemA linear system is a mathematical model of a system based on the use of a linear operator.Linear systems typically exhibit features and properties that are much simpler than the general, nonlinear case....
- Linear mediumLinear mediumA linear medium is any medium which is intended to be written to or accessed in a linear fashion, literally meaning in a line.This means that the information is written to or read from the medium in a given order, so for example a book containing a novel is intended to be read from front to back,...
- Linear programmingLinear programmingLinear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
- BilinearBilinearBilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
- Multilinear
- Linear motorLinear motorA linear motor is an electric motor that has had its stator and rotor "unrolled" so that instead of producing a torque it produces a linear force along its length...
- Linear ALinear ALinear A is one of two scripts used in ancient Crete before Mycenaean Greek Linear B; Cretan hieroglyphs is the second script. In Minoan times, before the Mycenaean Greek dominion, Linear A was the official script for the palaces and religious activities, and hieroglyphs were mainly used on seals....
and Linear BLinear BLinear B is a syllabic script that was used for writing Mycenaean Greek, an early form of Greek. It pre-dated the Greek alphabet by several centuries and seems to have died out with the fall of Mycenaean civilization...
scripts. - Linear interpolationLinear interpolationLinear interpolation is a method of curve fitting using linear polynomials. Lerp is an abbreviation for linear interpolation, which can also be used as a verb .-Linear interpolation between two known points:...