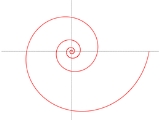
Logarithmic spiral
Encyclopedia
 |
 |
 |
 |
 |
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral
Spiral
In mathematics, a spiral is a curve which emanates from a central point, getting progressively farther away as it revolves around the point.-Spiral or helix:...
curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
which often appears in nature. The logarithmic spiral was first described by Descartes
René Descartes
René Descartes ; was a French philosopher and writer who spent most of his adult life in the Dutch Republic. He has been dubbed the 'Father of Modern Philosophy', and much subsequent Western philosophy is a response to his writings, which are studied closely to this day...
and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous spiral".
Definition
In polar coordinates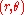
the logarithmic curve can be written as
or
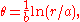
with
E (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
being the base of natural logarithms, and
and 
being arbitrary positive real constants.In parametric form, the curve is
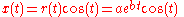
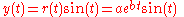
with real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s
and 
.The spiral has the property that the angle φ between the tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
and radial line
Radial line
This article is about the mathematical concept. For the medical meaning, see arterial line.A radial line is a line passing through the center of a circle or sphere. The correct "direction" of the radial line is from the radius point to a point on the arc or circle. This applies to its use in...
at the point
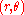is constant. This property can be expressed in differential geometric termsDifferential geometry of curves
Differential geometry of curves is the branch of geometry that dealswith smooth curves in the plane and in the Euclidean space by methods of differential and integral calculus....
as
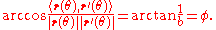
The derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of
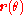is proportional to the parameter 
. In other words, it controls how "tightly" and in which direction the spiral spirals. In the extreme case that 
(
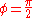) the spiral becomes a circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
of radius
. Conversely, in the limitLimit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
that
approaches infinityExtended real number line
In mathematics, the affinely extended real number system is obtained from the real number system R by adding two elements: +∞ and −∞ . The projective extended real number system adds a single object, ∞ and makes no distinction between "positive" or "negative" infinity...
(φ → 0) the spiral tends toward a straight half-line. The complement
Complementary angles
In geometry, complementary angles are angles whose measures sum to 90°. If the two complementary angles are adjacent their non-shared sides form a right angle....
of φ is called the pitch.
Spira mirabilis and Jacob Bernoulli
Spira mirabilis, LatinLatin
Latin is an Italic language originally spoken in Latium and Ancient Rome. It, along with most European languages, is a descendant of the ancient Proto-Indo-European language. Although it is considered a dead language, a number of scholars and members of the Christian clergy speak it fluently, and...
for "miraculous spiral", is another name for the logarithmic spiral. Although this curve had already been named by other mathematicians, the specific name ("miraculous" or "marvelous" spiral) was given to this curve by Jacob Bernoulli, because he was fascinated by one of its unique mathematical properties: the size of the spiral increases but its shape is unaltered with each successive curve, a property known as self-similarity
Self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...
. Possibly as a result of this unique property, the spira mirabilis has evolved in nature, appearing in certain growing forms such as nautilus
Nautilus
Nautilus is the common name of marine creatures of cephalopod family Nautilidae, the sole extant family of the superfamily Nautilaceae and of its smaller but near equal suborder, Nautilina. It comprises six living species in two genera, the type of which is the genus Nautilus...
shells and sunflower
Sunflower
Sunflower is an annual plant native to the Americas. It possesses a large inflorescence . The sunflower got its name from its huge, fiery blooms, whose shape and image is often used to depict the sun. The sunflower has a rough, hairy stem, broad, coarsely toothed, rough leaves and circular heads...
heads. Jakob Bernoulli wanted such a spiral engraved on his headstone
Headstone
A headstone, tombstone, or gravestone is a marker, usually stone, that is placed over a grave. In most cases they have the deceased's name, date of birth, and date of death inscribed on them, along with a personal message, or prayer.- Use :...
along with the phrase "Eadem mutata resurgo
Eadem mutata resurgo
Eadem mutata resurgo is a Latin phrase that literally translates to "Although changed, I shall arise the same." The phrase was first known to be used by Jakob Bernoulli , a member of the famous Swiss mathematical family, and appears on his tombstone in Basel...
" ("Although changed, I shall arise the same."), but, by error, an Archimedean spiral
Archimedean spiral
The Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
was placed there instead.
Properties
The logarithmic spiral can be distinguished from the Archimedean spiralArchimedean spiral
The Archimedean spiral is a spiral named after the 3rd century BC Greek mathematician Archimedes. It is the locus of points corresponding to the locations over time of a point moving away from a fixed point with a constant speed along a line which rotates with constant angular velocity...
by the fact that the distances between the turnings of a logarithmic spiral increase in geometric progression
Geometric progression
In mathematics, a geometric progression, also known as a geometric sequence, is a sequence of numbers where each term after the first is found by multiplying the previous one by a fixed non-zero number called the common ratio. For example, the sequence 2, 6, 18, 54, ... is a geometric progression...
, while in an Archimedean spiral these distances are constant.
Logarithmic spirals are self-similar in that they are self-congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
under all similarity transformations
Similarity (geometry)
Two geometrical objects are called similar if they both have the same shape. More precisely, either one is congruent to the result of a uniform scaling of the other...
(scaling them gives the same result as rotating them). Scaling by a factor
gives the same as the original, without rotation. They are also congruent to their own involuteInvolute
In the differential geometry of curves, an involute is a curve obtained from another given curve by attaching an imaginary taut string to the given curve and tracing its free end as it is wound onto that given curve; or in reverse, unwound. It is a roulette wherein the rolling curve is a straight...
s, evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
s, and the pedal curve
Pedal curve
In the differential geometry of curves, a pedal curve is a curve derived by construction from a given curve ....
s based on their centers.
Starting at a point
and moving inward along the spiral, one can circle the origin an unbounded number of times without reaching it; yet, the total distance covered on this path is finite; that is, the limitLimit (mathematics)
In mathematics, the concept of a "limit" is used to describe the value that a function or sequence "approaches" as the input or index approaches some value. The concept of limit allows mathematicians to define a new point from a Cauchy sequence of previously defined points within a complete metric...
as
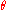goes toward 
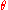is finite. This property was first realized by Evangelista TorricelliEvangelista Torricelli
Evangelista Torricelli was an Italian physicist and mathematician, best known for his invention of the barometer.-Biography:Evangelista Torricelli was born in Faenza, part of the Papal States...
even before calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
had been invented.
The total distance covered is
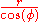, where 
is the straight-line distance from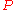 
to the origin.The exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
exactly maps all lines not parallel with the real or imaginary axis in the complex plane, to all logarithmic spirals in the complex plane with centre at 0. (Up to
Up to
In mathematics, the phrase "up to x" means "disregarding a possible difference in x".For instance, when calculating an indefinite integral, one could say that the solution is f "up to addition by a constant," meaning it differs from f, if at all, only by some constant.It indicates that...
adding integer multiples of
to the lines, the mapping of all lines to all logarithmic spirals is onto.) The pitch angle of the logarithmic spiral is the angle between the line and the imaginary axis.The function
, where the constant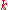 
is a complex numberComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
with non-zero imaginary part, maps the real line
Real line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
to a logarithmic spiral in the complex plane.
One can construct a golden spiral
Golden spiral
In geometry, a golden spiral is a logarithmic spiral whose growth factor is , the golden ratio. That is, a golden spiral gets wider by a factor of for every quarter turn it makes.-Formula:...
, a logarithmic spiral that grows outward by a factor of the golden ratio
Golden ratio
In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...
for every 90 degrees of rotation (pitch about 17.03239 degrees), or approximate it using Fibonacci number
Fibonacci number
In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....
s.
Logarithmic spirals in nature
In several natural phenomena one may find curves that are close to being logarithmic spirals. Here follows some examples and reasons:- The approach of a hawkHawkThe term hawk can be used in several ways:* In strict usage in Australia and Africa, to mean any of the species in the subfamily Accipitrinae, which comprises the genera Accipiter, Micronisus, Melierax, Urotriorchis and Megatriorchis. The large and widespread Accipiter genus includes goshawks,...
to its prey. Their sharpest view is at an angle to their direction of flight; this angle is the same as the spiral's pitch.
- The approach of an insect to a light source. They are used to having the light source at a constant angle to their flight path. Usually the sun (or moon for nocturnal species) is the only light source and flying that way will result in a practically straight line.
- The arms of spiral galaxiesGalaxyA galaxy is a massive, gravitationally bound system that consists of stars and stellar remnants, an interstellar medium of gas and dust, and an important but poorly understood component tentatively dubbed dark matter. The word galaxy is derived from the Greek galaxias , literally "milky", a...
. Our own galaxy, the Milky WayMilky WayThe Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
, has several spiral arms, each of which is roughly a logarithmic spiral with pitch of about 12 degrees.
- The nerves of the corneaCorneaThe cornea is the transparent front part of the eye that covers the iris, pupil, and anterior chamber. Together with the lens, the cornea refracts light, with the cornea accounting for approximately two-thirds of the eye's total optical power. In humans, the refractive power of the cornea is...
(this is, corneal nerves of the subepithelial layer terminate near superficial epithelial layer of the cornea in a logarithmic spiral pattern).
- The arms of tropical cycloneTropical cycloneA tropical cyclone is a storm system characterized by a large low-pressure center and numerous thunderstorms that produce strong winds and heavy rain. Tropical cyclones strengthen when water evaporated from the ocean is released as the saturated air rises, resulting in condensation of water vapor...
s, such as hurricanes.
- Many biologicalBiologyBiology is a natural science concerned with the study of life and living organisms, including their structure, function, growth, origin, evolution, distribution, and taxonomy. Biology is a vast subject containing many subdivisions, topics, and disciplines...
structures including the shells of molluskMolluscaThe Mollusca , common name molluscs or mollusksSpelled mollusks in the USA, see reasons given in Rosenberg's ; for the spelling mollusc see the reasons given by , is a large phylum of invertebrate animals. There are around 85,000 recognized extant species of molluscs. Mollusca is the largest...
s. In these cases, the reason may be construction from expanding similar shapes, as shown for polygonPolygonIn geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
al figures in the accompanying graphic.
- Logarithmic spiral beachesLogarithmic Spiral BeachesA logarithmic spiral beach is a type of beach which develops in the direction under which it is sheltered by a headland, in an area called the shadow zone. It is characterized as a logarithmic spiral because if you look at it in plan view or aerially, it represents the same shape that is created...
can form as the result of wave refraction and diffraction by the coast. Half Moon Bay, CaliforniaHalf Moon Bay, CaliforniaHalf Moon Bay is a coastal city in San Mateo County, California, USA. Its population was 11,324 as of the 2010 census. Immediately at the north of Half Moon Bay is the Pillar Point Harbor and the unincorporated community of Princeton-by-the-Sea....
is an example of such a type of beach.
External links
- Spira mirabilis history and math
- Astronomy Picture of the Day, Hurricane IsabelHurricane IsabelHurricane Isabel was the costliest and deadliest hurricane in the 2003 Atlantic hurricane season. The ninth named storm, fifth hurricane, and second major hurricane of the season, Isabel formed near the Cape Verde Islands from a tropical wave on September 6 in the tropical Atlantic Ocean...
vs. the Whirlpool GalaxyWhirlpool GalaxyThe Whirlpool Galaxy is an interacting grand-design spiral galaxy that is estimated to be 23 ± 4 million light-years from the Milky Way Galaxy. in the constellation Canes Venatici... - Astronomy Picture of the Day, Typhoon RammasunTyphoon Rammasun (2008)Typhoon Rammasun was recognized as the second typhoon of the 2008 Pacific typhoon season by the Japan Meteorological Agency and the Philippine Atmospheric, Geophysical and Astronomical Services Administration...
vs. the Pinwheel GalaxyPinwheel GalaxyThe Pinwheel Galaxy is a face-on spiral galaxy distanced 21 million light-years away in the constellation Ursa Major, first discovered by Pierre Méchain on March 27, 1781, and communicated to Charles Messier who verified its position for inclusion in the Messier Catalogue as one of its final... - SpiralZoom.com, an educational website about the science of pattern formation, spirals in nature, and spirals in the mythic imagination.
- Online exploration using JSXGraph (JavaScript)