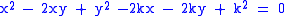.gif)
Envelope (mathematics)
Encyclopedia
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, an envelope of a family
Family of curves
A family of curves is a set of curves, each of which is given by a function or parametrization in which one or more of the parameters is variable. In general, the parameter influence the shape of the curve in a way that is more complicated than a simple linear transformation...
of curve
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
s in the plane is a curve that is tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
to each member of the family at some point. Classically, a point on the envelope can be thought of as the intersection of two "adjacent" curves, meaning the limit of intersections of nearby curves. This idea can be generalized to an envelope of surfaces in space, and so on to higher dimensions.
Envelope of a family of curves
Let each curve Ct in the family be given by ft(x, y)=0, where t is a parameter. Write F(t, x, y)=ft(x, y) and assume F is differentiable.The envelope of the family Ct is then defined as the set of points for which
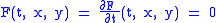
for some value of t,
where
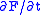is the partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of F with respect to t.
Note that if t and u, t≠u are two values of the parameter then the intersection of the curves Ct and Cu is given by
or equivalently
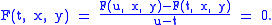
Letting u→t gives the definition above.
An important special case is when F(t, x, y) is a polynomial in t. This includes, by clearing denominators, the case where F(t, x, y) is a rational function in t. In this case, the definition amounts to t being a double root of F(t, x, y), so the equation of the envelope can be found by setting the discriminant
Discriminant
In algebra, the discriminant of a polynomial is an expression which gives information about the nature of the polynomial's roots. For example, the discriminant of the quadratic polynomialax^2+bx+c\,is\Delta = \,b^2-4ac....
of F to 0.
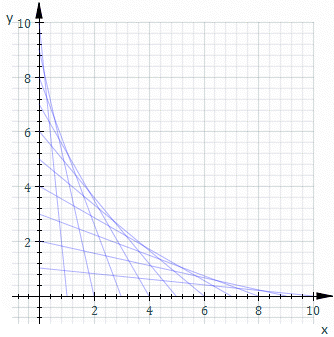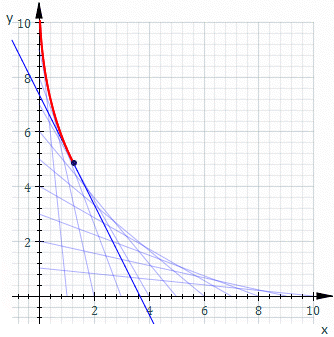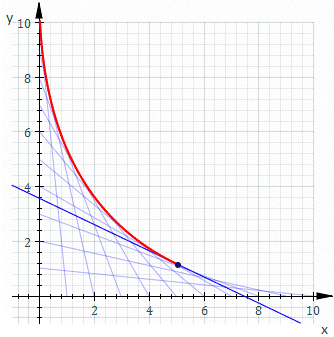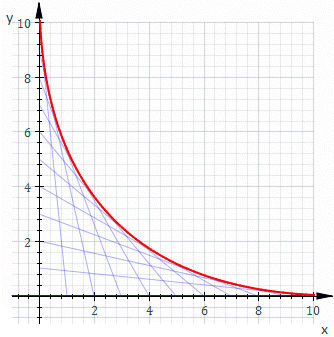
For example, let Ct be the line whose x and y intercepts are t and 1−t, this is shown in the animation above. The equation of Ct is
or, clearing fractions,
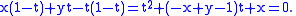
The equation of the envelope is then
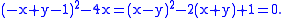
Often when F is not a rational function of the parameter it may be reduced to this case by an appropriate substitution. For example if the family is given by Cθ with an equation of the form u(x, y)cosθ+v(x, y)sinθ=w(x, y), then putting t=eiθ, cosθ=(t+1/t)/2, sinθ=(t-1/t)/2i changes the equation of the curve to
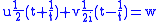
or
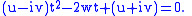
The equation of the envelope is then given by setting the discriminant to 0:
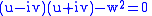
or
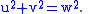
Alternative definitions
- The envelope E1 is the limit of intersections of nearby curves Ct.
- The envelope E2 is a curve tangent to all of the Ct.
- The envelope E3 is the boundary of the region filled by the curves Ct.
Then
, 
and 
Example 1
These four definitions of the discriminant, E1,E2, and E3, can lead to different sets. Consider for instance the curve parametrised by where . The one-parameter family of curves will be given by the tangent lines to γ.First we calculate the discriminant
. The generating function is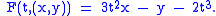
Calculating the partial derivative . It follows that either or . First assume that . Substituting into F:
and so, assuming that t ≠ 0, it follows that if and only if . Next, assuming that and substituting into F gives . So, assuming , it follows that if and only if . Thus the discriminant is the original curve and its tangent line at γ(0):
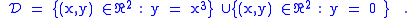
Next we calculate E1. One curve is given by and a nearby curve is given by where ε is some very small number. The intersection point comes from looking at the limit of as ε tends to zero. Notice that if and only if
If then L has only a single factor of ε. Assuming that then the intersection is given by
Since it follows that . The y value is calculated by knowing that this point must lie on a tangent line to the original curve γ: that . Substituting and solving gives y = t3. When , L is divisible by ε2. Assuming that then the intersection is given by
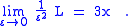
It follows that , and knowing that gives . It follows that
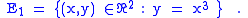
Next we calculate E2. The curve itself is the curve that is tangent to all of its own tangent lines. It follows that
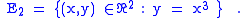
Finally we calculate E3. Every point in the plane has at least one tangent line to γ passing through it, and so region filled by the tangent lines is the whole plane. The boundary E3 is therefore the empty set. Indeed, consider a point in the plane, say (x0,y0). This point lies on a tangent line if and only if there exists a t such that
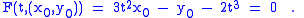
This is a cubic in t and as such has at least one real solution. It follows that at least one tangent line to γ must pass through any given point in the plane. If and then each point (x,y) has exactly one tangent line to γ passing through it. The same is true if . If and then each point (x,y) has exactly three distinct tangent lines to γ passing through it. The same is true if and . If and then each point (x,y) has exactly two tangent lines to γ passing through it (this corresponds to the cubic having one ordinary root and one repeated root). The same is true if and . If and , i.e., , then this point has a single tangent line to γ passing through it (this corresponds to the cubic having one real root of multiplicity 3). It follows that
Example 2
In string artString art
String art, or pin and thread art, is characterized by an arrangement of colored thread strung between points to form abstract geometric patterns or representational designs such as a ship's sails, sometimes with other artist material comprising the remainder of the work. Thread, wire, or string is...
it is common to cross-connect two lines of equally spaced pins. What curve is formed?
For simplicity, set the pins on the x- and y-axes; a non-orthogonal layout is a rotation and scaling
Scaling (geometry)
In Euclidean geometry, uniform scaling is a linear transformation that enlarges or shrinks objects by a scale factor that is the same in all directions. The result of uniform scaling is similar to the original...
away. A general straight-line thread connects the two points (0, k−t) and (t, 0), where k is an arbitrary scaling constant, and the family of lines is generated by varying the parameter t. From simple geometry, the equation of this straight line is y = −(k − t)x/t + k − t. Rearranging and casting in the form F(x,y,t) = 0 gives:
 |
(1) |
Now differentiate F(x,y,t) with respect to t and set the result equal to zero, to get
 |
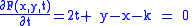(2) |
These two equations jointly define the equation of the envelope. From (2) we have t = (−y + x + k)/2. Substituting this value of t into (1) and simplifying gives an equation for the envelope in terms of x and y only:
This is the familiar implicit conic section
Conic section
In mathematics, a conic section is a curve obtained by intersecting a cone with a plane. In analytic geometry, a conic may be defined as a plane algebraic curve of degree 2...
form, in this case a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. Parabolae remain parabolae under rotation and scaling; thus the string art forms a parabolic arc ("arc" since only a portion of the full parabola is produced). In this case an anticlockwise rotation through 45° gives the orthogonal parabolic equation y = x2/(k√2) + k/(2√2). Note that the final step of eliminating t may not always be possible to do analytically, depending on the form of F(x,y,t).
Example 3
Let I ⊂ R be an open interval and let γ : I → R2 be a smooth plane curve parametrised by arc lengthArc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
. Consider the one-parameter family of normal lines to γ(I). A line is normal to γ at γ(t) if it passes through γ(t) and is perpendicular to the tangent vector to γ at γ(t). Let T denote the unit tangent vector to γ and let N denote the unit normal vector. Using a dot to denote the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, the generating family for the one-parameter family of normal lines is given by where
Clearly (x − γ)·T = 0 if and only if x − γ is perpendicular to T, or equivalently, if and only if x − γ is parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to N, or equivalently, if and only if x = γ + λN for some λ ∈ R. It follows that
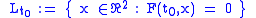
is exactly the normal line to γ at γ(t0). To find the discriminant of F we need to compute its partial derivative with respect to t:
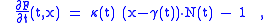
where κ is the plane curve curvature of γ. It has been seen that F = 0 if and only if x - γ = λN for some λ ∈ R. Assuming that F = 0 gives
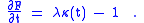
Assuming that κ ≠ 0 it follows that λ = 1/κ and so
This is exactly the evolute
Evolute
In the differential geometry of curves, the evolute of a curve is the locus of all its centers of curvature. Equivalently, it is the envelope of the normals to a curve....
of the curve γ.
Example 4
The following example generalizes the preceding one, and shows that in some cases the envelope of a family of curves may be seen as the topologic boundary of a union of sets, whose boundaries are the curves of the envelope. For
and 
consider the (open) right triangle in a Cartesian plane with vertices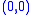 
, 
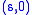and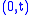 
Fix an exponent
, and consider the union of all the triangles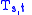 
subjected to the constraint 
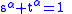, that is the open set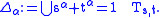
To write a Cartesian representation for
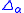, start with any 
, 
satisfying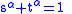 
and any 
. The Hölder inequality in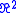 
with respect to the conjugated exponents 
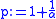and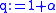 
gives:
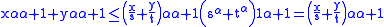,with equality if and only if
.In terms of a union of sets the latter inequality reads: the point
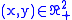belongs to the set 
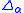, that is, it belongs to some 
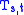with 
, if and only if it satisfies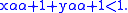
Moreover, the boundary in
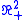of the set 
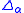is the envelope of the corresponding family of line segments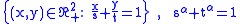
(that is, the hypotenuses of the triangles), and has Cartesian equation
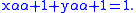
Notice that, in particular, the value
gives the arc of parabola of the example 1, and the value 
(meaning that all hypotenuses are unit length segments) gives the astroid.Envelope of a family of surfaces
A one-parameter family of surfaces in three-dimensional Euclidean space is given by a set of equations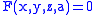
depending on a real parameter a. For example the tangent planes to a surface along a curve in the surface form such a family.
Two surfaces corresponding to different values a and a' intersect in a common curve defined by
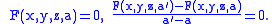
In the limit as a' approaches a, this curve tends to a curve contained in the surface at a
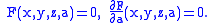
This curve is called the characteristic of the family at a. As a varies the locus of these characteristic curves defines a surface called the envelope of the family of surfaces.
Generalisations
The idea of an envelope of a family of smooth submanifolds follows naturally. In general, if we have a family of submanifolds with codimension c then we need to have at least a c-parameter family of such submanifolds. For example: a one-parameter family of curves in three-space (c = 2) does not, generically, have an envelope.Ordinary differential equation
Envelopes are connected to the study of ordinary differential equationOrdinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
s (ODEs), and in particular singular solution
Singular solution
A singular solution ys of an ordinary differential equation is a solution that is singular or one for which the initial value problem fails to have a unique solution at some point on the solution. The set on which a solution is singular may be as small as a single point or as large as the full...
s of ODEs. Consider, for example, the one-parameter family of tangent lines to the parabola y = x2. These are given by the generating family . The zero level set gives the equation of the tangent line to the parabola at the point (t0,t02). The equation can always be solved for y as a function of x and so, consider
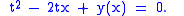
Differentiating and eliminating t gives the ODE
Not surprisingly y = 2tx − t2 are all solutions to this ODE. However, the envelope of this one-parameter family of lines, which is the parabola y = x2, is also a solution to this ODE. Another famous example is Clairaut's equation.
Partial differential equations
Envelopes can be used to construct more complicated solutions of first order partial differential equationPartial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s (PDEs) from simpler ones. Let F(x,u,Du) = 0 be a first order PDE, where x is a variable with values in an open set Ω ⊂ Rn, u is an unknown real-valued function, Du is the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of u, and F is a continuously differentiable function that is regular in Du. Suppose that u(x;a) is an m-parameter family of solutions: that is, for each fixed a ∈ A ⊂ Rm, u(x;a) is a solution of the differential equation. A new solution of the differential equation can be constructed by first solving (if possible)
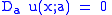
for a = φ(x) as a function of x. The envelope of the family of functions {u(·,a)}a∈A is defined by
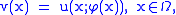
and also solves the differential equation (provided that it exists as a continuously differentiable function).
Geometrically, the graph of v(x) is everywhere tangent to the graph of some member of the family u(x;a). Since the differential equation is first order, it only puts a condition on the tangent plane to the graph, so that any function everywhere tangent to a solution must also be a solution. The same idea underlies the solution of a first order equation as an integral of the Monge cone
Monge cone
In the mathematical theory of partial differential equations , the Monge cone is a geometrical object associated with a first-order equation. It is named for Gaspard Monge. In two dimensions, letF = 0\qquad\qquad...
. The Monge cone is a cone field in the Rn+1 of the (x,u) variables cut out by the envelope of the tangent spaces to the first order PDE at each point. A solution of the PDE is then an envelope of the cone field.
In Riemannian geometry
Riemannian geometry
Riemannian geometry is the branch of differential geometry that studies Riemannian manifolds, smooth manifolds with a Riemannian metric, i.e. with an inner product on the tangent space at each point which varies smoothly from point to point. This gives, in particular, local notions of angle, length...
, if a smooth family of geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s through a point P in a Riemannian manifold
Riemannian manifold
In Riemannian geometry and the differential geometry of surfaces, a Riemannian manifold or Riemannian space is a real differentiable manifold M in which each tangent space is equipped with an inner product g, a Riemannian metric, which varies smoothly from point to point...
has an envelope, then P has a conjugate point where any geodesic of the family intersects the envelope. The same is true more generally in the calculus of variations
Calculus of variations
Calculus of variations is a field of mathematics that deals with extremizing functionals, as opposed to ordinary calculus which deals with functions. A functional is usually a mapping from a set of functions to the real numbers. Functionals are often formed as definite integrals involving unknown...
: if a family of extremals to a functional through a given point P has an envelope, then a point where an extremal intersects the envelope is a conjugate point to P.
Caustics
Geometrical optics
Geometrical optics, or ray optics, describes light propagation in terms of "rays". The "ray" in geometric optics is an abstraction, or "instrument", which can be used to approximately model how light will propagate. Light rays are defined to propagate in a rectilinear path as far as they travel in...
, a caustic
Caustic (optics)
In optics, a caustic or caustic network is the envelope of light rays reflected or refracted by a curved surface or object, or the projection of that envelope of rays on another surface. The caustic is a curve or surface to which each of the light rays is tangent, defining a boundary of an...
is the envelope of a family of light rays. In this picture there is an arc of a circle. The light rays (shown in blue) are coming from a source at infinity, and so arrive parallel. When they hit the circular arc the light rays are scattered in different directions according to the law of reflection
Specular reflection
Specular reflection is the mirror-like reflection of light from a surface, in which light from a single incoming direction is reflected into a single outgoing direction...
. When a light ray hits the arc at a point the light will be reflected as though it had been reflected by the arc's tangent line at that point. The reflected light rays give a one-parameter family of lines in the plane. The envelope of these lines is the reflective caustic
Caustic (optics)
In optics, a caustic or caustic network is the envelope of light rays reflected or refracted by a curved surface or object, or the projection of that envelope of rays on another surface. The caustic is a curve or surface to which each of the light rays is tangent, defining a boundary of an...
. A reflective caustic will generically consist of smooth points and ordinary cusp
Cusp
Cusp may refer to:*Beach cusps, a pointed and regular arc pattern of the shoreline at the beach*Behavioral cusp an important behavior change with far reaching consequences*Cusp catastrophe...
points.
From the point of view of the calculus of variations, Fermat's principle
Fermat's principle
In optics, Fermat's principle or the principle of least time is the principle that the path taken between two points by a ray of light is the path that can be traversed in the least time. This principle is sometimes taken as the definition of a ray of light...
(in its modern form) implies that light rays are the extremals for the length functional
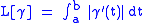
among smooth curves γ on [a,b] with fixed endpoints γ(a) and γ(b). The caustic determined by a given point P (in the image the point is at infinity) is the set of conjugate points to P.