
Cnoidal wave
Encyclopedia

Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, a cnoidal wave is a nonlinear and exact periodic
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
wave
Wave
In physics, a wave is a disturbance that travels through space and time, accompanied by the transfer of energy.Waves travel and the wave motion transfers energy from one point to another, often with no permanent displacement of the particles of the medium—that is, with little or no associated mass...
solution of the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
. These solutions are in terms of the Jacobi elliptic function cn, which is why they are coined cnoidal waves. They are used to describe surface gravity waves of fairly long wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
, as compared to the water depth.
The cnoidal wave solutions were derived by Korteweg
Diederik Korteweg
Diederik Johannes Korteweg was a Dutch mathematician. He is now remembered as the joint discoverer of the Korteweg–de Vries equation.-Early life and education:...
and de Vries
Gustav de Vries
Gustav de Vries was a Dutch mathematician, who is best remembered for his work on the Korteweg–de Vries equation with Diederik Korteweg. He was born on 22 January 1866 in Amsterdam, and studied at the University of Amsterdam with the distinguished physical chemist Johannes van der Waals and with...
, in their 1895 paper in which they also propose their dispersive
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
long-wave equation, now known as the Korteweg–de Vries equation. In the limit of infinite wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
, the cnoidal wave becomes a solitary wave.
The Benjamin–Bona–Mahony equation has improved short-wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
behaviour, as compared to the Korteweg–de Vries equation, and is another uni-directional wave equation with cnoidal wave solutions. Further, since the Korteweg–de Vries equation is an approximation to the Boussinesq equations for the case of one-way wave propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
, cnoidal waves are approximate solutions to the Boussinesq equations.
Cnoidal wave solutions can appear in other applications than surface gravity waves as well, for instance to describe ion acoustic wave
Ion acoustic wave
An ion acoustic wave is one type of longitudinal oscillation of the ions and electrons in a plasma, much like acoustic waves traveling in neutral gas. However, because the waves propagate through positively charged ions, ion acoustic waves can interact with their electromagnetic fields, as well as...
s in plasma physics.
Korteweg–de Vries, and Benjamin–Bona–Mahony equations
The Korteweg–de Vries equationKorteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
(KdV equation) can be used to describe the uni-directional propagation of weakly nonlinear and long waves—where long wave means: having long wavelengths as compared with the mean water depth—of surface gravity waves on a fluid layer. The KdV equation is a dispersive
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
wave equation, including both frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
dispersion and amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
dispersion effects. In its classical use, the KdV equation is applicable for wavelengths λ in excess of about five times the average
Average
In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average....
water depth h, so for λ > 5 h; and for the period
Periodic function
In mathematics, a periodic function is a function that repeats its values in regular intervals or periods. The most important examples are the trigonometric functions, which repeat over intervals of length 2π radians. Periodic functions are used throughout science to describe oscillations,...
τ greater than
 with g the strength of the gravitational acceleration
with g the strength of the gravitational accelerationEarth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
. To envisage the position of the KdV equation within the scope of classical wave approximations, it distinguishes itself in the following ways:
- Korteweg–de Vries equation — describes the forward propagation of weakly nonlinear and dispersive waves, for long waves with λ > 7 h.
- Shallow water equationsShallow water equationsThe shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes...
— are also nonlinear and do have amplitude dispersion, but no frequency dispersion; they are valid for very long waves, λ > 20 h. - Boussinesq equations — have the same range of validity as the KdV equation (in their classical form), but allow for wave propagation in arbitrary directions, so not only forward-propagating waves. The drawback is that the Boussinesq equations are often more difficult to solve than the KdV equation; and in many applications wave reflections are small and may be neglected.
- Airy wave theoryAiry wave theoryIn fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
— has full frequency dispersion, so valid for arbitrary depth and wavelength, but is a linear theory without amplitude dispersion, limited to low-amplitude waves. - Stokes' wave theory — a perturbation-series approach to the description of weakly nonlinear and dispersive waves, especially successful in deeper water for relative short wavelengths, as compared to the water depth. However, for long waves the Boussinesq approach—as also applied in the KdV equation—is often preferred. This is because in shallow water the Stokes' perturbation series needs many terms before convergence towards the solution, due to the peaked crestCrest (physics)A crest is the point on a wave with the maximum value or upward displacement within a cycle. A trough is the opposite of a crest, so the minimum or lowest point in a cycle.-Interference:...
s and long flat troughs of the nonlinear waves. While the KdV or Boussinesq models give good approximations for these long nonlinear waves.
The KdV equation can be derived from the Boussinesq equations, but additional assumptions are needed to be able to split-off of the forward wave propagation. For practical applications, the Benjamin–Bona–Mahony equation (BBM equation) is preferable over the KdV equation, a forward-propagating model similar to KdV but with much better frequency-dispersion behaviour at shorter wavelengths. Further improvements in short-wave performance can be obtained by starting to derive a one-way wave equation from a modern improved Boussinesq model, valid for even shorter wavelengths.
Cnoidal waves
The cnoidal wave solutions of the KdV equation were presented by Korteweg and de Vries in their 1895 paper, which article is based on the PhD thesis by de Vries in 1894. Solitary wave solutions for nonlinear and dispersive long waves had been found earlier by Boussinesq in 1872, and RayleighJohn Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
in 1876. The search for these solutions was triggered by the observations of this solitary wave (or "wave of translation") by Russell
John Scott Russell
John Scott Russell was a Scottish naval engineer who built the Great Eastern in collaboration with Isambard Kingdom Brunel, and made the discovery that gave birth to the modern study of solitons.-Personal life:John Scott Russell was born John Russell on 9 May 1808 in Parkhead, Glasgow, the son of...
, both in nature and laboratory experiments. Cnoidal wave solutions of the KdV equation are stable with respect to small perturbations.
The surface elevation η(x,t), as a function of horizontal position x and time t, for a cnoidal wave is given by:
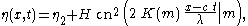
where H is the wave height
Wave height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
, λ is the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
, c is the phase speed and η2 is the trough elevation. Further cn is one of the Jacobi elliptic functions and K(m) is the complete elliptic integral of the first kind; both are dependent on the elliptic parameter m. The latter, m, determines the shape of the cnoidal wave. For m equal to zero the cnoidal wave becomes a cosine function, while for values close to one the cnoidal wave gets peaked crest
Crest (physics)
A crest is the point on a wave with the maximum value or upward displacement within a cycle. A trough is the opposite of a crest, so the minimum or lowest point in a cycle.-Interference:...
s and (very) flat troughs.
An important dimensionless parameter for nonlinear long waves (λ h) is the Ursell parameter:

For small values of U, say U < 5, a linear theory can be used, and at higher values nonlinear theories have to be used, like cnoidal wave theory. The demarcation zone between—third or fifth order—Stokes' and cnoidal wave theories is in the range 10–25 of the Ursell parameter. As can be seen from the formula for the Ursell parameter, for a given relative wave height H/h the Ursell parameter—and thus also the nonlinearity—grows quickly with increasing relative wavelength λ/h.
Based on the analysis of the full nonlinear problem of surface gravity waves within potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
theory, the above cnoidal waves can be considered the lowest-order term in a perturbation series. Higher-order cnoidal wave theories remain valid for shorter and more nonlinear waves. A fifth-order cnoidal wave theory was developed by Fenton in 1979. A detailed description and comparison of fifth-order Stokes' and fifth-order cnoidal wave theories is given in the review article by Fenton.
Cnoidal wave descriptions, through a renormalisation, are also well suited to waves on deep water, even infinite water depth; as found by Clamond. A description of the interactions of cnoidal waves in shallow water, as found in real seas, has been provided by Osborne in 1994.
Korteweg–de Vries equation
The Korteweg–de Vries equationKorteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
(KdV equation), as used for water waves and in dimensional form, is:
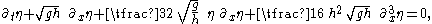
where
| η | : surface elevation Elevation The elevation of a geographic location is its height above a fixed reference point, most commonly a reference geoid, a mathematical model of the Earth's sea level as an equipotential gravitational surface .... , a function of x and t, with the positive direction upwards (opposing gravity), |
| x | : horizontal coordinate, |
| t | : time, |
| g | : the value of Earth's gravity Earth's gravity The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram... , |
| h | : the mean Average In mathematics, an average, or central tendency of a data set is a measure of the "middle" value of the data set. Average is one form of central tendency. Not all central tendencies should be considered definitions of average.... water depth, and |
| ∂x and ∂t | : partial derivative Partial derivative In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant... operators with respect to x and t. |
Non-dimensionalisation
All quantities can be made dimensionless
Dimensionless quantity
In dimensional analysis, a dimensionless quantity or quantity of dimension one is a quantity without an associated physical dimension. It is thus a "pure" number, and as such always has a dimension of 1. Dimensionless quantities are widely used in mathematics, physics, engineering, economics, and...
using the gravitational acceleration g and water depth h:
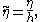
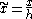 and
and 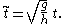
The resulting non-dimensional form of the KdV equation is
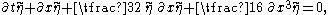
In the remainder, the tilde
Tilde
The tilde is a grapheme with several uses. The name of the character comes from Portuguese and Spanish, from the Latin titulus meaning "title" or "superscription", though the term "tilde" has evolved and now has a different meaning in linguistics....
s will be dropped for ease of notation.
Relation to a standard form
The form
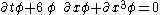
is obtained through the transformation

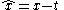 and
and 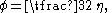
but this form will not be used any further in this derivation.
Fixed-form propagating waves
Periodic wave solutions, travelling with phase speed c, are sought. These permanent waves have to be of the following:
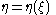 with
with 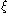 the wave phase
the wave phasePhase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
:
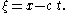
Consequently, the partial derivatives with respect to space and time become:
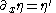 and
and 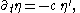
where η’ denotes the ordinary derivative of η(ξ) with respect to the argument
Parameter
Parameter from Ancient Greek παρά also “para” meaning “beside, subsidiary” and μέτρον also “metron” meaning “measure”, can be interpreted in mathematics, logic, linguistics, environmental science and other disciplines....
ξ.
Using these in the KdV equation, the following third-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
is obtained:
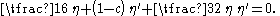
Integration to a first-order ordinary differential equation
This can be integrated
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
once, to obtain:
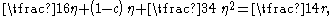
with r an integration constant. After multiplying with 4 η’, and integrating once more
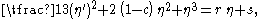
with s another integration constant. This is written in the form
The cubic polynomial f(η) becomes negative for large positive values of η, and positive for large negative values of η. Since the surface elevation η is real valued
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, also the integration constants r and s are real. The polynomial f can be expressed in terms of its roots η1, η2 and η3:
Because f(η) is real valued, the three roots η1, η2 and η3 are either all three real, or otherwise one is real and the remaining two are a pair of complex conjugate
Complex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
s. In the latter case, with only one real-valued root, there is only one elevation η at which f(η) is zero. And consequently also only one elevation at which the surface slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
η’ is zero. However, we are looking for wave like solutions, with two elevations—the wave crest
Crest (physics)
A crest is the point on a wave with the maximum value or upward displacement within a cycle. A trough is the opposite of a crest, so the minimum or lowest point in a cycle.-Interference:...
and trough (physics)—where the surface slope is zero. The conclusion is that all three roots of f(η) have to be real valued.
Without loss of generality, its is assumed that the three real roots are ordered as:
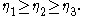
Solution of the first-order ordinary-differential equation
Now, from equation it can be seen that only real values for the slope exist if f(η) is positive. This corresponds with η2 ≤ η≤ η1, which therefore is the range between which the surface elevation oscillates, see also the graph of f(η). This condition is satisfied with the following representation of the elevation η(ξ):
in agreement with the periodic character of the sought wave solutions and with ψ(ξ) the phase of the trigonometric functions sin and cos. From this form, the following descriptions of various terms in equations and can be obtained:
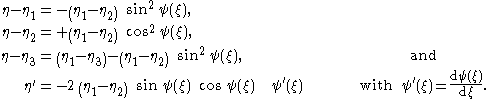
Using these in equations and , the following ordinary differential equation relating ψ and ξ is obtained, after some manipulations:
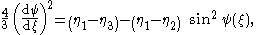
with the right hand side still positive, since η1 − η3 ≥ η1 − η2. Without loss of generality, we can assume that ψ(ξ) is a monotone function, since f(η) has no zeros in the interval η2 < η < η1. So the above ordinary differential equation can also be solved in terms of ξ(ψ) being a function of ψ:
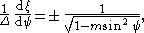
with:
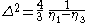 and
and 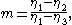
where m is the so-called elliptic parameter, satisfying 0 ≤ m ≤ 1 (because η3 ≤ η2 ≤ η1).
If ξ = 0 is chosen at the wave crest η(0) = η1 integration gives
with F(ψ|m) the incomplete elliptic integral of the first kind. The Jacobi elliptic functions cn and sn are inverses of F(ψ|m) given by
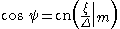 and
and 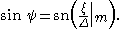
With the use of equation , the resulting cnoidal-wave solution of the KdV equation is found
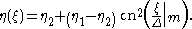
What remains, is to determine the parameters: η1, η2, Δ and m.
Relationships between the cnoidal-wave parameters
First, since η1 is the crest elevation and η2 is the trough elevation, it is convenient to introduce the wave height
Wave height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
, defined as H = η1 − η2. Consequently, we find for m and for Δ:
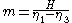 and
and  so
so 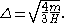
The cnoidal wave solution can be written as:
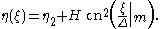
Second, the trough is located at ψ = ½ π, so the distance between ξ = 0 and ξ = ½ λ is, with λ the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
, from equation :
 giving
giving 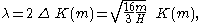
where K(m) is the complete elliptic integral of the first kind. Third, since the wave oscillates around the mean water depth, the average value of η(ξ) has to be zero. So
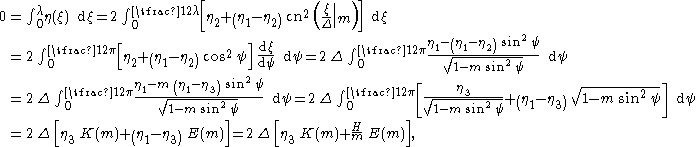
where E(m) is the complete elliptic integral of the second kind. The following expressions for η1, η2 and η3 as a function of the elliptic parameter m and wave height H result:
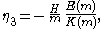
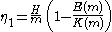 and
and 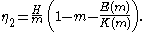
Fourth, from equations and a relationship can be established between the phase speed c and the roots η1, η2 and η3:
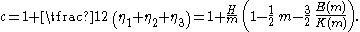
The relative phase-speed changes are depicted in the figure below. As can be seen, for m > 0.96 (so for 1 −m < 0.04) the phase speed increases with increasing wave height H. This corresponds with the longer and more nonlinear waves. The nonlinear change in the phase speed, for fixed m, is proportional to the wave height H. Note that the phase speed c is related to the wavelength λ and period τ as:
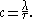
Résumé of the solution
All quantities here will be given in their dimensional forms, as valid for surface gravity waves before non-dimensionalisation.
The cnoidal-wave solution of the KdV equation is:
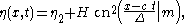
with H the wave height
Wave height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
—the difference between crest
Crest (physics)
A crest is the point on a wave with the maximum value or upward displacement within a cycle. A trough is the opposite of a crest, so the minimum or lowest point in a cycle.-Interference:...
and trough elevation, η2 the trough elevation, m the elliptic parameter, c the phase speed and cn one of the Jacobi elliptic functions. The trough level η2 and width parameter Δ can be expressed in terms of H, h and m:
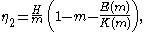 and
and 
with K(m) the complete elliptic integral of the first kind and E(m) the complete elliptic integral of the second kind. Note that K(m) and E(m) are denoted here as a function of the elliptic parameter m and not as a function of the elliptic modulus k, with m = k2.
The wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ, phase speed c and wave period τ are related to H, h and m by:

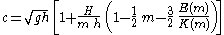 and
and 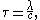
with g the Earth's gravity
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
.
Most often, the known wave parameters are the wave height H, mean water depth h, gravitational acceleration g, and either the wavelength λ or else the period τ. Then the above relations for λ, c and τ are used to find the elliptic parameter m. This requires numerical solution by some iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
.
Benjamin–Bona–Mahony equation
The Benjamin–Bona–Mahony equation (BBM equation), or regularised long wave (RLW) equation, is in dimensional form given by: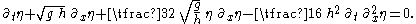
All quantities have the same meaning as for the KdV equation. The BBM equation is often preferred over the KdV equation because it has a better short-wave behaviour.
Derivation
The derivation is analogous to the one for the KdV equation. The dimensionless BBM equation is, non-dimensionalised using mean water depth h and gravitational acceleration g:
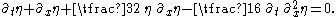
This can be brought into the standard form
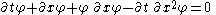
through the transformation:

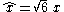 and
and 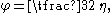
but this standard form will not be used here.
Analogue to the drivation of the cnoidal wave solution for the KdV equation, periodic wave solutions η(ξ), with ξ = x−ct are considered Then the BBM equation becomes a third-order ordinary differential equation, which can be integrated twice, to obtain:
 with
with 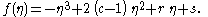
Which only differs from the equation for the KdV equation through the factor c in front of (η′)2 in the left hand side. Through a coordinate transformation β = ξ /
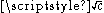 the factor c may be removed, resulting in the same first-order ordinary differential equation for both the KdV and BBM equation. However, here the form given in the preceding equation is used. This results in a different formulation for Δ as found for the KdV equation:
the factor c may be removed, resulting in the same first-order ordinary differential equation for both the KdV and BBM equation. However, here the form given in the preceding equation is used. This results in a different formulation for Δ as found for the KdV equation:
The relation of the wavelength λ, as a function of H and m, is affected by this change in
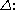
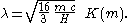
For the rest, the derivation is analogous to the one for the KdV equation, and will not be repeated here.
Résumé
The results are presented in dimensional form, for water waves on a fluid layer of depth h.
The cnoidal wave solution of the BBM equation, together with the associated relationships for the parameters is:

The only difference with the cnoidal wave solution of the KdV equation is in the equation for the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ. For practical applications, usually the water depth h, wave height
Wave height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
H, gravitational acceleration
Earth's gravity
The gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
g, and either the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ, or—most often—the period (physics) τ are provided. Then the elliptic parameter m has to be determined from the above relations for λ, c and τ through some iterative method
Iterative method
In computational mathematics, an iterative method is a mathematical procedure that generates a sequence of improving approximate solutions for a class of problems. A specific implementation of an iterative method, including the termination criteria, is an algorithm of the iterative method...
.
Example
In this example, a cnoidal wave according to the Korteweg–de Vries (KdV) equation is considered. The following parameters of the wave are given:- mean water depth h = 5 m (16.4 ft),
- wave heightWave heightIn fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
H = 3 m (9.8 ft), - wave period τ = 7 sSecondThe second is a unit of measurement of time, and is the International System of Units base unit of time. It may be measured using a clock....
, and - gravitational accelerationEarth's gravityThe gravity of Earth, denoted g, refers to the acceleration that the Earth imparts to objects on or near its surface. In SI units this acceleration is measured in metres per second per second or equivalently in newtons per kilogram...
g = 9.81 m/s2 (32 ft/s2).
Instead of the period τ, in other cases the wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ may occur as a quantity known beforehand.
First, the dimensionless period is computed:
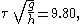
which is larger than seven, so long enough for cnoidal theory to be valid. The main unknown is the elliptic parameter m. This has to be determined in such a way that the wave period τ, as computed from cnoidal wave theory for the KdV equation:

 and
and 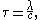
is consistent with the given value of τ; here λ is the wavelength and c is the phase speed of the wave. Further, K(m) and E(m) are complete elliptic integrals of the first and second kind, respectively. Searching for the elliptic parameter m can be done by trial and error
Trial and error
Trial and error, or trial by error, is a general method of problem solving, fixing things, or for obtaining knowledge."Learning doesn't happen from failure itself but rather from analyzing the failure, making a change, and then trying again."...
, or by use of a numerical root-finding algorithm
Root-finding algorithm
A root-finding algorithm is a numerical method, or algorithm, for finding a value x such that f = 0, for a given function f. Such an x is called a root of the function f....
. In this case, starting from an initial guess minit = 0.99, by trial and error the answer
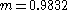
is found. Within the process, the wavelength λ and phase speed c have been computed:
- wavelength λ = 50.8 m (166.7 ft), and
- phase speed c = 7.26 m/s (23.8 ft/s).
The phase speed c can be compared with its value
 according to the shallow water equations
according to the shallow water equationsShallow water equations
The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes...
:
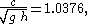
showing a 3.8% increase due to the effect of nonlinear amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
dispersion
Dispersion (water waves)
In fluid dynamics, dispersion of water waves generally refers to frequency dispersion, which means that waves of different wavelengths travel at different phase speeds. Water waves, in this context, are waves propagating on the water surface, and forced by gravity and surface tension...
, which wins in this case from the reduction of phase speed by frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
dispersion.
Now the wavelength is known, the Ursell number
Ursell number
In fluid dynamics, the Ursell number indicates the nonlinearity of long surface gravity waves on a fluid layer. This dimensionless parameter is named after Fritz Ursell, who discussed its significance in 1953....
can be computed as well:
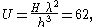
which is not small, so linear wave theory
Airy wave theory
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
is not applicable, but cnoidal wave theory is. Finally, the ratio of wavelength to depth is λ / h = 10.2 > 7, again indicating this wave is long enough to being considered as a cnoidal wave.
Solitary-wave limit
For very long nonlinear waves, with the parameter m close to one, m → 1, the Jacobi elliptic function cn can be approximated by with
with 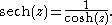
Here sinh, cosh, tanh and sech are hyperbolic function
Hyperbolic function
In mathematics, hyperbolic functions are analogs of the ordinary trigonometric, or circular, functions. The basic hyperbolic functions are the hyperbolic sine "sinh" , and the hyperbolic cosine "cosh" , from which are derived the hyperbolic tangent "tanh" and so on.Just as the points form a...
s. In the limit m = 1:
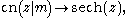
with sech(z) = 1 / cosh(z).
Further, for the same limit of m → 1, the complete elliptic integral of the first kind K(m) goes to infinity, while the complete elliptic integral of the second kind E(m) goes to one. This implies that the limiting values of the phase speed c and minimum elevelation η2 become:
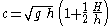 and
and 
Consequently, in terms of the width parameter Δ, the solitary wave solution to both the KdV and BBM equation is:
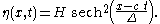
The width parameter, as found for the cnoidal waves and now in the limit m → 1, is different for the KdV and the BBM equation:
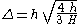 |
: KdV equation, and |
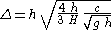 |
: BBM equation. |
But the phase speed of the solitary wave in both equations is the same, for a certain combination of height H and depth h.
Limit of infinitesimal wave height
For infinitesimalInfinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
wave height the results of cnoidal wave theory are expected to converge towards those of Airy wave theory
Airy wave theory
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
for the limit of long waves λ h. First the surface elevation, and thereafter the phase speed, of the cnoidal waves for infinitesimal wave height will be examined.
Surface elevation
The Jacobi elliptic function cn can be expanded into a Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...

K’(m) is known as the imaginary quarter period, while K(m) is also called the real quarter period of the Jacobi elliptic function. They are related through: K’(m) = K(1−m)
Since the interest here is in small wave height, corresponding with small parameter m 1, it is convenient to consider the Maclaurin series for the relevant parameters, to start with the complete elliptic integrals K and E:
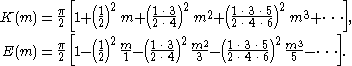
Then the hyperbolic-cosine terms, appearing in the Fourier series, can be expanded for small m 1 as follows:
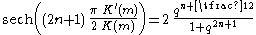 with the nome q given by
with the nome q given by 
The nome q has the following behaviour for small m:
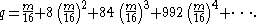
Consequently, the amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
s of the first terms in the Fourier series are:
 |
: |  |
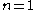 |
: |  |
 |
: | 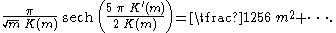 |
So, for m 1 the Jacobi elliptic function has the first Fourier series terms:
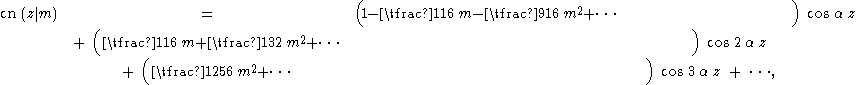 with
with 
And its square is

The free surface η(x,t) of the cnoidal wave will be expressed in its Fourier series, for small values of the elliptic parameter m. First, note that the argument of the cn function is ξ/Δ, and that the wavelength λ = 2 Δ K(m), so:
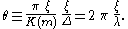
Further, the mean free-surface elevation is zero. Therefore, the surface elevation of small amplitude waves is
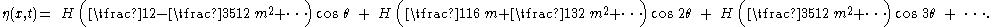
Also the wavelength λ can be expanded into a Maclaurin series of the elliptic parameter m, differently for the KdV and the BBM equation, but this is not necessary for the present purpose.
| Note: The limiting behaviour for zero m—at infinitesimal wave height—can also be seen from: |
| m), which is 4 K(m), and the period 2π for the cosine cos(z). The above Fourier series for small m does not have this drawback, and is consistent with forms as found using the Lindstedt–Poincaré method in perturbation theory Perturbation theory Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem... . |
For infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
wave height, in the limit m → 0, the free-surface elevation becomes:
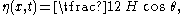 with
with 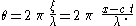
So the wave amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
is ½H, half the wave height
Wave height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
. This is of the same form as studied in Airy wave theory
Airy wave theory
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
, but note that cnoidal wave theory is only valid for long waves with their wavelength much longer than the average water depth.
Phase speed
The phase speed of a cnoidal wave, both for the KdV and BBM equation, is given by: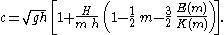
In this formulation the phase speed is a function of wave height
Wave height
In fluid dynamics, the wave height of a surface wave is the difference between the elevations of a crest and a neighbouring trough. Wave height is a term used by mariners, as well as in coastal, ocean and naval engineering....
H and parameter m. However, for the determination of wave propagation for waves of infinitesimal height, it is necessary to determine the behaviour of the phase speed at constant wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
λ in the limit that the parameter m approaches zero. This can be done by using the equation for the wavelength, which is different for the KdV and BBM equation:
| KdV : |  |
| BBM : |  |
Introducing the relative wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
κh:
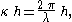
and using the above equations for the phase speed and wavelength, the factor H / m in the phase speed can be replaced by κh and m. The resulting phase speeds are:
| KdV : |  |
| BBM : |  |
The limiting behaviour for small m can be analysed through the use of the Maclaurin series for K(m) and E(m), resulting in the following expression for the common factor in both formulas for c:
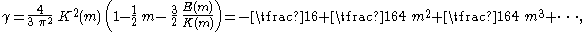
so in the limit m → 0, the factor γ → −. The limiting value of the phase speed for m 1 directly results.
The phase speeds for infinitesimal wave height, according to the cnoidal wave theories for the KdV equation and BBM equation, are
| KdV | : | 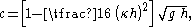 |
| BBM | : |  |
with κ = 2π / λ the wavenumber
Wavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
and κh the relative wavenumber. These phase speeds are in full agreement with the result obtained by directly searching for sine-wave solutions of the linearised KdV and BBM equations. As is evident from these equations, the linearised BBM equation has a positive phase speed for all κh. On the other hand, the phase speed of the linearised KdV equation changes sign for short waves with κh >
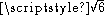 . This is in conflict with the derivation of the KdV equation as a one-way wave equation.
. This is in conflict with the derivation of the KdV equation as a one-way wave equation.Direct derivation from the full inviscid-flow equations
Cnoidal waves can be derived directly from the inviscidViscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
, irrotational and incompressible
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
flow equations, and expressed in terms of three invariants of the flow, as shown by . In a frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
moving with the phase speed, in which reference frame the flow becomes a steady flow, the cnoidal wave solutions can directly be related to the mass flux
Mass flux
Mass flux is the rate of mass flow across a unit area .-See also:*Flux*Fick's law*Darcy's law...
, momentum flux and energy head of the flow. Following —using a stream function
Stream function
The stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
description of this incompressible flow—the horizontal and vertical components of the flow velocity are +∂zΨ and −∂ξΨ, in the ξ and z direction respectively (ξ = x−ct). The vertical coordinate z is positive in the upward direction, opposite to the direction of the gravitational acceleration, and the zero level of z is at the impermeable lower boundary of the fluid domain. While the free surface is at z = ζ(ξ); note that ζ is the local water depth, related to the surface elevation η(ξ) as ζ = h + η with h the mean water depth.
In this steady flow, the discharge
Discharge
Discharge in the context to expel or to "let go" may refer to:* A military discharge, issued when a member of the armed forces is released from service* Termination of employment, the end of an employee's duration with an employer...
Q through each vertical cross section is a constant independent of ξ, and because of the horizontal bed also the horizontal momentum flux S, divided by the density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
ρ, through each vertical cross section is conserved. Further, for this inviscid and irrotational flow, Bernoulli's principle
Bernoulli's principle
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
can be applied and has the same Bernoulli constant R everywhere in the flow domain. They are defined as:
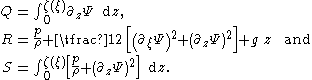
For fairly long waves, assuming the water depth ζ is small compared to the wavelength λ, the following relation is obtained between the water depth ζ(ξ) and the three invariants Q, R and S:
This nonlinear and first-order ordinary differential equation
Ordinary differential equation
In mathematics, an ordinary differential equation is a relation that contains functions of only one independent variable, and one or more of their derivatives with respect to that variable....
has cnoidal wave solutions.
For very long waves of infinitesimal
Infinitesimal
Infinitesimals have been used to express the idea of objects so small that there is no way to see them or to measure them. The word infinitesimal comes from a 17th century Modern Latin coinage infinitesimus, which originally referred to the "infinite-th" item in a series.In common speech, an...
amplitude
Amplitude
Amplitude is the magnitude of change in the oscillating variable with each oscillation within an oscillating system. For example, sound waves in air are oscillations in atmospheric pressure and their amplitudes are proportional to the change in pressure during one oscillation...
on a fluid of depth h and with a uniform flow velocity v, the flow constants are according to the shallow water equations
Shallow water equations
The shallow water equations are a set of hyperbolic partial differential equations that describe the flow below a pressure surface in a fluid .The equations are derived from depth-integrating the Navier–Stokes...
:
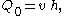
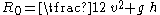 and
and 
Equation can be brought into non-dimensional form by use of the discharge Q and gravitational acceleration g, and defining the critical depth hc:

related to the critical flow demarcation between subcritical flow and supercritical flow
Supercritical flow
A supercritical flow is when the flow velocity is larger than the wave velocity. The analogous condition in gas dynamics is supersonic....
(see also Froude number
Froude number
The Froude number is a dimensionless number defined as the ratio of a characteristic velocity to a gravitational wave velocity. It may equivalently be defined as the ratio of a body's inertia to gravitational forces. In fluid mechanics, the Froude number is used to determine the resistance of an...
). Consequently, the non-dimensional form of the equation is
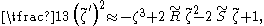
with
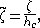
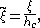
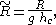 and
and 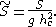
Derivation
First eliminate the pressure p from the momentum flux S by use of the Bernoulli equation: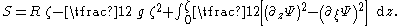
The streamfunction Ψ is expanded as a Maclaurin series around the bed at z = 0, and using that the impermeable bed is a streamline and the irrotationality of the flow: Ψ = 0 and ∂z2Ψ = 0 at z = 0:
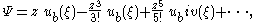
with ub the horizontal velocity at the bed z = 0. Because the waves are long, h ≫ λ, only terms up to z3 and ζ3 are retained in the approximations to Q and S. The momentum flux S then becomes:
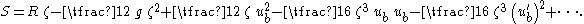
The discharge Q becomes, since it is the value of the streamfunction Ψ at the free surface z = ζ:
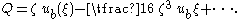
As can be seen, the discharge Q is an O(ζ) quantity. From this, the bed velocity is seen to be
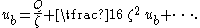
Note that Q / ζ is an order one quantity. This relation will be used to replace the bed velocity ub by Q and ζ in the momentum flux S. The following terms can be derived from it:
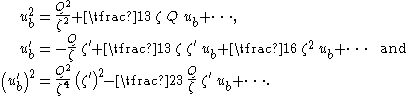
Consequently, the momentum flux S becomes, again retaining only terms up to proportional to ζ3:

Which can directly be recast in the form of equation .
Potential energy
The potential energy density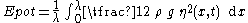
with ρ the fluid density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, is one of the infinite number of invariant
Invariant (mathematics)
In mathematics, an invariant is a property of a class of mathematical objects that remains unchanged when transformations of a certain type are applied to the objects. The particular class of objects and type of transformations are usually indicated by the context in which the term is used...
s of the KdV equation. This can be seen by multiplying the KdV equation with the surface elevation η(x,t); after repeated use of the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
the result is:
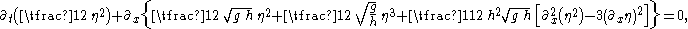
which is in conservation form, and is an invariant after integration over the interval of periodicity—the wavelength for a cnoidal wave. The potential energy is not an invariant of the BBM equation, but ½ρg [η2 + h2 (∂x η)2] is.
First the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the surface elevation in a cnoidal wave is computed. Note that η2 = −(1/λ) 0∫λ H cn2(ξ/Δ|m) dx, cn(ξ/Δ|m) = cos ψ(ξ) and λ = 2 Δ K(m), so
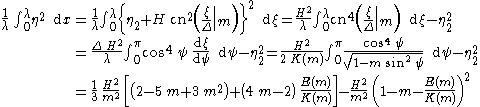
The potential energy, both for the KdV and the BBM equation, is subsequently found to be
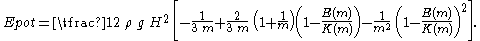
The infinitesimal wave-height limit (m → 0) of the potential energy is Epot = ρ g H2, which is in agreement with Airy wave theory
Airy wave theory
In fluid dynamics, Airy wave theory gives a linearised description of the propagation of gravity waves on the surface of a homogeneous fluid layer. The theory assumes that the fluid layer has a uniform mean depth, and that the fluid flow is inviscid, incompressible and irrotational...
. The wave height is twice the amplitude, H = 2a, in the infinitesimal wave limit.

