
Dispersion relation
Encyclopedia
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
and electrical engineering
Electrical engineering
Electrical engineering is a field of engineering that generally deals with the study and application of electricity, electronics and electromagnetism. The field first became an identifiable occupation in the late nineteenth century after commercialization of the electric telegraph and electrical...
, dispersion most often refers to frequency-dependent effects in wave propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
. Note, however, that there are several other uses of the word "dispersion" in the physical sciences.
In the presence of dispersion, wave velocity
Wave velocity
Wave velocity is a wave property, which may refer to:*phase velocity, the velocity at which a wave phase propagates at a certain frequency*pulse wave velocity, the velocity at which a pulse travels through a medium, usually applied to arteries as a measure of arterial stiffness*group velocity, the...
is no longer uniquely defined, giving rise to the distinction of phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
and group velocity
Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
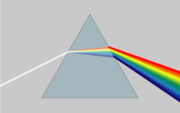
. A well-known effect of phase velocity dispersion is the color dependence of light refraction
Refraction
Refraction is the change in direction of a wave due to a change in its speed. It is essentially a surface phenomenon . The phenomenon is mainly in governance to the law of conservation of energy. The proper explanation would be that due to change of medium, the phase velocity of the wave is changed...
that can be observed in prisms
Prism (optics)
In optics, a prism is a transparent optical element with flat, polished surfaces that refract light. The exact angles between the surfaces depend on the application. The traditional geometrical shape is that of a triangular prism with a triangular base and rectangular sides, and in colloquial use...
and rainbow
Rainbow
A rainbow is an optical and meteorological phenomenon that causes a spectrum of light to appear in the sky when the Sun shines on to droplets of moisture in the Earth's atmosphere. It takes the form of a multicoloured arc...
s.
Dispersion relations describe the interrelations of wave properties like wavelength
Wavelength
In physics, the wavelength of a sinusoidal wave is the spatial period of the wave—the distance over which the wave's shape repeats.It is usually determined by considering the distance between consecutive corresponding points of the same phase, such as crests, troughs, or zero crossings, and is a...
, frequency
Frequency
Frequency is the number of occurrences of a repeating event per unit time. It is also referred to as temporal frequency.The period is the duration of one cycle in a repeating event, so the period is the reciprocal of the frequency...
, velocities, and refractive index
Refractive index
In optics the refractive index or index of refraction of a substance or medium is a measure of the speed of light in that medium. It is expressed as a ratio of the speed of light in vacuum relative to that in the considered medium....
. Besides geometry- and material-dependent dispersion relations, there are the overarching Kramers–Kronig relations that connect the frequency dependences of propagation and attenuation.
Dispersion may be caused either by geometric boundary conditions (waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
s, shallow water) or by interaction of the waves with the transmitting medium. Elementary particles, considered as matter waves, have a nontrivial dispersion relation even in the absence of geometric constraints and other media.
Dispersion
Dispersion occurs when pure plane waves of different wavelengths have different propagation velocities, so that a wave packetWave packet
In physics, a wave packet is a short "burst" or "envelope" of wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere...
of mixed wavelengths tends to spread out in space. The speed of a plane wave, v, is a function of the wave's wavelength
 :
:
The wave's speed, wavelength, and frequency, f, are related by the dispersion relation

Dispersion relations are more commonly expressed in terms of the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
 and wavenumber
and wavenumberWavenumber
In the physical sciences, the wavenumber is a property of a wave, its spatial frequency, that is proportional to the reciprocal of the wavelength. It is also the magnitude of the wave vector...
 . Rewriting the relation above in these variables gives
. Rewriting the relation above in these variables gives
The use of ω(k) to describe the dispersion relation is standard because both the phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
ω/k and the group velocity
Group velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
dω/dk have convenient representations via this function.
The elementary sorts of waves being considered can be described by

where
- A is the amplitude of the wave,
- A0 = A(0,0),
- x is a position along the wave's direction of travel, and
- t is the time at which the wave is described.
Plane waves in vacuum
Plane waves in vacuum are the simplest case of wave propagation: no geometric constraint, no interaction with a transmitting medium.Electromagnetic waves
For electromagnetic waves in vacuum, the frequency is proportional to the wavenumber:
This is a linear dispersion relation. In this case, phase velocity and group velocity are the same:

they are given by c, the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
in vacuum, a frequency-independent constant.
De Broglie dispersion relations

which in the ultrarelativistic limit is essentially
and in the nonrelativistic limit is

where in both equations
 is the rest mass. In the nonrelativistic limit,
is the rest mass. In the nonrelativistic limit,  is essentially constant and
is essentially constant and  is the familiar kinetic energy in terms of momentum
is the familiar kinetic energy in terms of momentum  .
.The transition from ultrarelativistic
Ultrarelativistic limit
In physics, a particle is called ultrarelativistic when its speed is very close to the speed of light c.Max Planck showed that the relativistic expression for the energy of a particle whose rest mass is m and momentum is p is given by E^2 = m^2 c^4 + p^2 c^2...
to nonrelativistic behaviour shows up as a slope change from p to p2 as shown in the log-log dispersion plot of E vs. p.
Elementary particles, atomic nuclei, atoms, and even molecules behave in some context as matter waves. According to the de Broglie relations, their kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
E can be expressed as a frequency ω, and their momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
p as a wavenumber k, using the reduced Planck constant
Planck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
ħ:
Accordingly, frequency and wavenumber are connected through a dispersion relation,
which in the nonrelativistic limit reads
| Animation: phase and group velocity of electrons |
|---|
 |
Frequency versus wavenumber
As mentioned above, when the focus in a medium is on refraction rather than absorption i.e. on the real part of the refractive index, it is common to refer to the functional dependence of frequency on wavenumber as the dispersion relation. For particles, this translates to a knowledge of energy as a function of momentum.Waves and optics
The name "dispersion relation" originally comes from opticsOptics
Optics is the branch of physics which involves the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behavior of visible, ultraviolet, and infrared light...
. It is possible to make the effective speed of light dependent on wavelength by making light pass through a material which has a non-constant index of refraction, or by using light in a non-uniform medium such as a waveguide
Waveguide
A waveguide is a structure which guides waves, such as electromagnetic waves or sound waves. There are different types of waveguides for each type of wave...
. In this case, the waveform will spread over time, such that a narrow pulse will become an extended pulse, i.e. be dispersed. In these materials,
 is known as the group velocity
is known as the group velocityGroup velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
and corresponds to the speed at which the peak propagates, a value different from the phase velocity
Phase velocity
The phase velocity of a wave is the rate at which the phase of the wave propagates in space. This is the speed at which the phase of any one frequency component of the wave travels. For such a component, any given phase of the wave will appear to travel at the phase velocity...
.
Deep water waves

Ocean surface wave
In fluid dynamics, wind waves or, more precisely, wind-generated waves are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They usually result from the wind blowing over a vast enough stretch of fluid surface. Waves in the...
is often written as

where g is the acceleration due to gravity. Deep water, in this respect, is commonly denoted as the case where the water depth is larger than half the wavelength. In this case the phase velocity is

and the group velocity is

Waves on a string


where T is the tension force in the string and μ is the string's mass per unit length.
As for the case of electromagnetic waves in a vacuum, ideal strings are thus a
non-dispersive medium i.e. the phase and group velocities are equal and independent
(to first order) of vibration frequency.
Solid state
In the study of solids, the study of the dispersion relation of electrons is of paramount importance. The periodicity of crystals means that many levels of energyFermi surface
In condensed matter physics, the Fermi surface is an abstract boundary useful for predicting the thermal, electrical, magnetic, and optical properties of metals, semimetals, and doped semiconductors. The shape of the Fermi surface is derived from the periodicity and symmetry of the crystalline...
are possible for a given momentum and that some energies might not be available at any momentum. The collection of all possible energies and momenta is known as the band structure of a material. Properties of the band structure define whether the material is an insulator
Electrical insulation
thumb|250px|[[Coaxial Cable]] with dielectric insulator supporting a central coreThis article refers to electrical insulation. For insulation of heat, see Thermal insulation...
, semiconductor
Semiconductor
A semiconductor is a material with electrical conductivity due to electron flow intermediate in magnitude between that of a conductor and an insulator. This means a conductivity roughly in the range of 103 to 10−8 siemens per centimeter...
or conductor.
Phonons
Phonons are to sound waves in a solid what photons are to light: They are the quanta that carry it. The dispersion relation of phononPhonon
In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, such as solids and some liquids...
s is also important and non-trivial. Most systems will show two separate bands on which phonons live. Phonons on the band that cross the origin are known as acoustic phonons, the others as optical phonons.
Electron optics
With high energy (e.g. 200 keV) electrons in a transmission electron microscope, the energy dependence of higher order Laue zone (HOLZ) lines in convergent beam electron diffractionElectron diffraction
Electron diffraction refers to the wave nature of electrons. However, from a technical or practical point of view, it may be regarded as a technique used to study matter by firing electrons at a sample and observing the resulting interference pattern...
(CBED) patterns allows one, in effect, to directly image cross-sections of a crystal's three-dimensional dispersion surface
Brillouin zone
In mathematics and solid state physics, the first Brillouin zone is a uniquely defined primitive cell in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice. It is found by the same method as for the Wigner–Seitz cell in the Bravais lattice...
. This dynamical effect
Dynamical theory of diffraction
The dynamical theory of diffraction describes the interaction of waves with a regular lattice. The wave fields traditionally described are X-rays, neutrons or electrons and the regular lattice, atomic crystal structures or nanometer scaled multi-layers or self arranged systems...
has found application in the precise measurement of lattice parameters, beam energy, and more recently for the electronics industry: lattice strain.
History
Isaac NewtonIsaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
studied refraction in prisms. He failed, however, to recognize the material dependence of the dispersion relation. Had he done so, he would almost certainly have invented the achromatic lens
Achromatic lens
An achromatic lens or achromat is a lens that is designed to limit the effects of chromatic and spherical aberration. Achromatic lenses are corrected to bring two wavelengths into focus in the same plane....
.
Dispersion of waves on water was studied by Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
in 1776.
The universality of the Kramers-Kronig relation
Kramers-Kronig relation
The Kramers–Kronig relations are bidirectional mathematical relations, connecting the real and imaginary parts of any complex function that is analytic in the upper half-plane...
s (1926/27) became apparent with subsequent papers on the dispersion relation's connection to causality in the scattering theory
Scattering theory
In mathematics and physics, scattering theory is a framework for studying and understanding the scattering of waves and particles. Prosaically, wave scattering corresponds to the collision and scattering of a wave with some material object, for instance sunlight scattered by rain drops to form a...
of all types of waves and particles.
External links
- Poster on CBED simulations to help visualize dispersion surfaces, by Andrey Chuvilin and Ute Kaiser





