
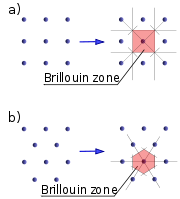
Brillouin zone
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and solid state physics, the first Brillouin zone is a uniquely defined primitive cell
Primitive cell
Used predominantly in geometry, solid state physics, and mineralogy, particularly in describing crystal structure, a primitive cell is a minimum cell corresponding to a single lattice point of a structure with translational symmetry in 2 dimensions, 3 dimensions, or other dimensions...
in reciprocal space. The boundaries of this cell are given by planes related to points on the reciprocal lattice
Reciprocal lattice
In physics, the reciprocal lattice of a lattice is the lattice in which the Fourier transform of the spatial function of the original lattice is represented. This space is also known as momentum space or less commonly k-space, due to the relationship between the Pontryagin duals momentum and...
. It is found by the same method as for the Wigner–Seitz cell
Wigner–Seitz cell
The Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a type of Voronoi cell used in the study of crystalline material in solid-state physics....
in the Bravais lattice. The importance of the Brillouin zone stems from the Bloch wave
Bloch wave
A Bloch wave or Bloch state, named after Felix Bloch, is the wavefunction of a particle placed in a periodic potential...
description of waves in a periodic medium, in which it is found that the solutions can be completely characterized by their behavior in a single Brillouin zone.
Taking surfaces at the same distance from one element of the lattice and its neighbours, the volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
included is the first Brillouin zone (see the derivation of the Wigner-Seitz cell
Wigner-Seitz cell
The Wigner–Seitz cell, named after Eugene Wigner and Frederick Seitz, is a type of Voronoi cell used in the study of crystalline material in solid-state physics....
). Another definition is as the set of points in k-space that can be reached from the origin without crossing any Bragg plane
Bragg's law
In physics, Bragg's law gives the angles for coherent and incoherent scattering from a crystal lattice. When X-rays are incident on an atom, they make the electronic cloud move as does any electromagnetic wave...
. Equivalently, this is the Voronoi cell around the origin of the reciprocal lattice.
There are also second, third, etc., Brillouin zones, corresponding to a sequence of disjoint regions (all with the same volume) at increasing distances from the origin, but these are used more rarely. As a result, the first Brillouin zone is often called simply the Brillouin zone. (In general, the n-th Brillouin zone consists of the set of points that can be reached from the origin by crossing exactly n − 1 distinct Bragg planes.)
A related concept is that of the irreducible Brillouin zone, which is the first Brillouin zone reduced by all of the symmetries in the point group
Point group
In geometry, a point group is a group of geometric symmetries that keep at least one point fixed. Point groups can exist in a Euclidean space with any dimension, and every point group in dimension d is a subgroup of the orthogonal group O...
of the lattice.
The concept of a Brillouin zone was developed by Léon Brillouin
Léon Brillouin
Léon Nicolas Brillouin was a French physicist. He made contributions to quantum mechanics, radio wave propagation in the atmosphere, solid state physics, and information theory.-Early life:...
(1889–1969), a French physicist.
Critical points
.svg.png)
| Symbol | Description |
|---|---|
| Γ | Center of the Brillouin zone |
| Simple cube | |
| M | Center of an edge |
| R | Corner point |
| X | Center of a face |
| Face-centered cubic | |
| K | Middle of an edge joining two hexagonal faces |
| L | Center of a hexagonal face |
| U | Middle of an edge joining a hexagonal and a square face |
| W | Corner point |
| X | Center of a square face |
| Body-centered cubic | |
| H | Corner point joining four edges |
| N | Center of a face |
| P | Corner point joining three edges |
| Hexagonal | |
| A | Center of a hexagonal face |
| H | Corner point |
| K | Middle of an edge joining two rectangular faces |
| L | Middle of an edge joining a hexagonal and a rectangular face |
| M | Center of a rectangular face |
Other lattices have different types of high-symmetry points. They can be found in the illustrations below.
Triclinic lattice system TRI(4)
See below for the aflowlib.org standard.
Monoclinic lattice system MCL(1), MCLC(5)
See below for the aflowlib.org standard.
Orthorhombic lattice system ORC(1), ORCC(1), ORCI(1), ORCF(3)
See below for the aflowlib.org standard.
Tetragonal lattice system TET(1), BCT(2)
See below for the aflowlib.org standard.
Rhombohedral lattice system RHL(2)
See below for the aflowlib.org standard.
Hexagonal lattice system HEX(1)
See below for the aflowlib.org standard.
Cubic lattice system CUB(1), BCC(1), FCC(1)
 |
 |
 |
See below for the aflowlib.org standard.

