
Triangle group
Encyclopedia
In mathematics
, a triangle group is a group
that can be realized geometrically by sequences of reflections
across the sides of a triangle
. The triangle can be an ordinary Euclidean
triangle, a triangle on the sphere
, or a hyperbolic triangle
. Each triangle group is the symmetry group
of a tiling
of the Euclidean plane, the sphere
, or the Hyperbolic plane
by congruent
triangles, a fundamental domain
for the action, called a Möbius triangle.
s greater than or equal to 2. A triangle group Δ(l,m,n) is a group of motions of the Euclidean plane, the two-dimensional sphere, the real projective plane, or the hyperbolic plane generated by the reflection
s in the sides of a triangle
with angles π/l, π/m and π/n (measured in radian
s). The product of the reflections in two adjacent sides is a rotation
by the angle which is twice the angle between those sides, 2π/l, 2π/m and 2π/n Therefore, if the generating reflections are labeled a, b, c and the angles between them in the cyclic order are as given above, then the following relations hold:
It is a theorem that all other relations between a, b, c are consequences of these relations and that Δ(l,m,n) is a discrete group
of motions of the corresponding space. Thus a triangle group is a reflection group
that admits a group presentation

An abstract group with this presentation is a Coxeter group
with three generators.
: it is Euclidean if the angle sum is exactly π, spherical if it exceeds π and hyperbolic if it is strictly smaller than π. Moreover, any two triangles with the given angles are congruent. Each triangle group determines a tiling, which is conventionally colored in two colors, so that any two adjacent tiles have opposite colors.
In terms of the numbers l, m, n > 1 there are the following possibilities.

The triangle group is the infinite symmetry group
of a certain tessellation
(or tiling) of the Euclidean plane by triangles whose angles add up to π (or 180°). Up to permutations, the triple (l, m, n) is one of the triples (2,3,6), (2,4,4), (3,3,3). The corresponding triangle groups are instances of wallpaper group
s.
More detailed diagrams, labeling the vertices and showing how reflection operates, are given as follows:

The triangle group is the finite symmetry group of a tiling of a unit sphere by spherical triangles, or Möbius triangles, whose angles add up to a number greater than π. Up to permutations, the triple (l,m,n) has the form (2,3,3), (2,3,4), (2,3,5), or (2,2,n), n>1. Spherical triangle groups can be identified with the symmetry groups of regular polyhedra
in the three-dimensional Euclidean space: Δ(2,3,3) corresponds to the tetrahedron
, Δ(2,3,4) to both the cube
and the octahedron
(which have the same symmetry group), Δ(2,3,5) to both the dodecahedron and the icosahedron
. The groups Δ(2,2,n), n>1 of dihedral symmetry can be interpreted as the symmetry groups of the family of dihedron
s, which are degenerate solids formed by two identical regular n-gons
joined together, or dually hosohedrons, which are formed by joining n digon
s together at two vertices.
The spherical tiling corresponding to a regular polyhedron is obtained by forming the barycentric subdivision
of the polyhedron and projecting the resulting points and lines onto the circumscribed sphere. In the case of the tetrahedron, there are four faces and each face is an equilateral triangle that is subdivided into 6 smaller pieces by the medians intersecting in the center. The resulting tesselation has 4 × 6=24 spherical triangles (it is the spherical disdyakis cube).
These groups are finite, which corresponds to the compactness of the sphere – areas of discs in the sphere initially grow in terms of radius, but eventually cover the entire sphere.
The triangular tilings are depicted below:
Spherical tilings corresponding to the octahedron and the icosahedron and dihedral spherical tilings with even n are centrally symmetric. Hence each of them determines a tiling of the real projective plane, an elliptic tiling. Its symmetry group is the quotient of the spherical triangle group by the reflection through the origin (-I), which is a central element of order 2. Since the projective plane is a model of elliptic geometry
, such groups are called elliptic triangle groups.

The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane
by hyperbolic triangles whose angles add up to a number less than π. All triples not already listed represent tilings of the hyperbolic plane. For example, the triple (2,3,7) produces the (2,3,7) triangle group
. There are infinitely many such groups; the tilings associated with some small values:
Hyperbolic triangle groups are examples of non-Euclidean crystallographic group
and have been generalized in the theory of Gromov hyperbolic group
s.
of index
2 in Δ(l,m,n) generated by words of even length in the generators. Such subgroups are sometimes referred to as "ordinary" triangle groups or von Dyck groups, after Walther von Dyck
. For spherical, Euclidean, and hyperbolic triangles, these correspond to the elements of the group that preserve the orientation of the triangle – the group of rotations. For projective (elliptic) triangles, they cannot be so interpreted, as the projective plane is non-orientable, so there is no notion of "orientation-preserving". The reflections are however locally orientation-reversing (and every manifold is locally orientable, because locally Euclidean): they fix a line and at each point in the line are a reflection across the line.
The groups D(l,m,n) is defined by the following presentation:
In terms of the generators above, these are x = ab, y = ca, yx = cb. Geometrically, the three elements x, y, xy correspond to rotations by 2π/l, 2π/m and 2π/n about the three vertices of the triangle.
Note that D(l,m,n) ≅ D(m,l,n) ≅ D(n,m,l), so D(l,m,n) is independent of the order of the l,m,n.
A hyperbolic von Dyck group is a Fuchsian group
, a discrete group consisting of orientation-preserving isometries of the hyperbolic plane.
for the action (the triangle defined by the lines of reflection), called a Möbius triangle, and are given by a triple of integers, (l,m,n), – integers correspond to (2l,2m,2n) triangles coming together at a vertex. There are also tilings by overlapping triangles, which correspond to Schwarz triangle
s with rational numbers (l/a,m/b,n/c), where the denominators are coprime
to the numerators. This corresponds to edges meeting at angles of aπ/l (resp.), which corresponds to a rotation of 2aπ/l (resp.), which has order l and is thus identical as an abstract group element, but distinct when represented by a reflection.
For example, the Schwartz triangle (2 3 3) yields a density
1 tiling of the sphere, while the triangle (2 3/2 3) yields a density 3 tiling of the sphere, but with the same abstract group. These symmetries of overlapping tilings are not considered triangle groups.
in 1856, in his paper on Icosian Calculus
.
is generated by two elements, S and T, subject to the relations S² = (ST)³ = 1 (no relation on T), is the rotational triangle group (2,3,∞) and maps onto all triangle groups (2,3,n) by adding the relation Tn = 1. More generally, the Hecke group Hq is by two elements, S and T, subject to the relations S² = (ST)q = 1 (no relation on T), is the rotational triangle group (2,q,∞), and maps onto all triangle groups (2,q,n) by adding the relation Tn = 1 the modular group is the Hecke group H3. In Grothendieck
's theory of dessins d'enfants, a Belyi function gives rise to a tessellation of a Riemann surface
by reflection domains of a triangle group.
All 26 sporadic group
s are quotients of triangle groups, of which 12 are Hurwitz groups (quotients of the (2,3,7) group).
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a triangle group is a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
that can be realized geometrically by sequences of reflections
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
across the sides of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
. The triangle can be an ordinary Euclidean
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
triangle, a triangle on the sphere
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
, or a hyperbolic triangle
Hyperbolic triangle
In mathematics, the term hyperbolic triangle has more than one meaning.-Hyperbolic geometry:In hyperbolic geometry, a hyperbolic triangle is a figure in the hyperbolic plane, analogous to a triangle in Euclidean geometry, consisting of three sides and three angles...
. Each triangle group is the symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a tiling
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the Euclidean plane, the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, or the Hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
by congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
triangles, a fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
for the action, called a Möbius triangle.
Definition
Let l, m, n be integerInteger
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s greater than or equal to 2. A triangle group Δ(l,m,n) is a group of motions of the Euclidean plane, the two-dimensional sphere, the real projective plane, or the hyperbolic plane generated by the reflection
Reflection (mathematics)
In mathematics, a reflection is a mapping from a Euclidean space to itself that is an isometry with a hyperplane as set of fixed points; this set is called the axis or plane of reflection. The image of a figure by a reflection is its mirror image in the axis or plane of reflection...
s in the sides of a triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
with angles π/l, π/m and π/n (measured in radian
Radian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s). The product of the reflections in two adjacent sides is a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
by the angle which is twice the angle between those sides, 2π/l, 2π/m and 2π/n Therefore, if the generating reflections are labeled a, b, c and the angles between them in the cyclic order are as given above, then the following relations hold:
It is a theorem that all other relations between a, b, c are consequences of these relations and that Δ(l,m,n) is a discrete group
Discrete group
In mathematics, a discrete group is a group G equipped with the discrete topology. With this topology G becomes a topological group. A discrete subgroup of a topological group G is a subgroup H whose relative topology is the discrete one...
of motions of the corresponding space. Thus a triangle group is a reflection group
Reflection group
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
that admits a group presentation

An abstract group with this presentation is a Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
with three generators.
Classification
Given any natural numbers l, m, n > 1 exactly one of the classical two-dimensional geometries (Euclidean, spherical, or hyperbolic) admits a triangle with the angles (π/l, π/m, π/n), and the space is tiled by reflections of the triangle. The sum of the angles of the triangle determines the type of the geometry by the Gauss–Bonnet theoremGauss–Bonnet theorem
The Gauss–Bonnet theorem or Gauss–Bonnet formula in differential geometry is an important statement about surfaces which connects their geometry to their topology...
: it is Euclidean if the angle sum is exactly π, spherical if it exceeds π and hyperbolic if it is strictly smaller than π. Moreover, any two triangles with the given angles are congruent. Each triangle group determines a tiling, which is conventionally colored in two colors, so that any two adjacent tiles have opposite colors.
In terms of the numbers l, m, n > 1 there are the following possibilities.
The Euclidean case

The triangle group is the infinite symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of a certain tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
(or tiling) of the Euclidean plane by triangles whose angles add up to π (or 180°). Up to permutations, the triple (l, m, n) is one of the triples (2,3,6), (2,4,4), (3,3,3). The corresponding triangle groups are instances of wallpaper group
Wallpaper group
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s.
More detailed diagrams, labeling the vertices and showing how reflection operates, are given as follows:
The spherical case

The triangle group is the finite symmetry group of a tiling of a unit sphere by spherical triangles, or Möbius triangles, whose angles add up to a number greater than π. Up to permutations, the triple (l,m,n) has the form (2,3,3), (2,3,4), (2,3,5), or (2,2,n), n>1. Spherical triangle groups can be identified with the symmetry groups of regular polyhedra
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
in the three-dimensional Euclidean space: Δ(2,3,3) corresponds to the tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
, Δ(2,3,4) to both the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
and the octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
(which have the same symmetry group), Δ(2,3,5) to both the dodecahedron and the icosahedron
Icosahedron
In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
. The groups Δ(2,2,n), n>1 of dihedral symmetry can be interpreted as the symmetry groups of the family of dihedron
Dihedron
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...
s, which are degenerate solids formed by two identical regular n-gons
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
joined together, or dually hosohedrons, which are formed by joining n digon
Digon
In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...
s together at two vertices.
The spherical tiling corresponding to a regular polyhedron is obtained by forming the barycentric subdivision
Barycentric subdivision
In geometry, the barycentric subdivision is a standard way of dividing an arbitrary convex polygon into triangles, a convex polyhedron into tetrahedra, or, in general, a convex polytope into simplices with the same dimension, by connecting the barycenters of their faces in a specific way.The name...
of the polyhedron and projecting the resulting points and lines onto the circumscribed sphere. In the case of the tetrahedron, there are four faces and each face is an equilateral triangle that is subdivided into 6 smaller pieces by the medians intersecting in the center. The resulting tesselation has 4 × 6=24 spherical triangles (it is the spherical disdyakis cube).
These groups are finite, which corresponds to the compactness of the sphere – areas of discs in the sphere initially grow in terms of radius, but eventually cover the entire sphere.
The triangular tilings are depicted below:
 (2,2,2) |
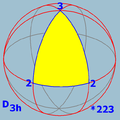 (3,2,2) |
... (p,2,2) |
|---|---|---|
 (3,3,2) |
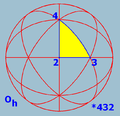 (4,3,2) |
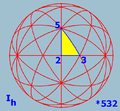 (5,3,2) |
Spherical tilings corresponding to the octahedron and the icosahedron and dihedral spherical tilings with even n are centrally symmetric. Hence each of them determines a tiling of the real projective plane, an elliptic tiling. Its symmetry group is the quotient of the spherical triangle group by the reflection through the origin (-I), which is a central element of order 2. Since the projective plane is a model of elliptic geometry
Elliptic geometry
Elliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
, such groups are called elliptic triangle groups.
The hyperbolic case

The triangle group is the infinite symmetry group of a tiling of the hyperbolic plane
Uniform tilings in hyperbolic plane
There are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...
by hyperbolic triangles whose angles add up to a number less than π. All triples not already listed represent tilings of the hyperbolic plane. For example, the triple (2,3,7) produces the (2,3,7) triangle group
(2,3,7) triangle group
In the theory of Riemann surfaces and hyperbolic geometry, the triangle group is particularly important. This importance stems from its connection to Hurwitz surfaces, namely Riemann surfaces of genus g with the largest possible order, 84, of its automorphism group.A note on terminology – the "...
. There are infinitely many such groups; the tilings associated with some small values:
Hyperbolic triangle groups are examples of non-Euclidean crystallographic group
Non-Euclidean crystallographic group
In mathematics, a non-Euclidean crystallographic group, NEC group or N.E.C. group is a discrete group of isometries of the hyperbolic plane. These symmetry groups correspond to the wallpaper groups in euclidean geometry...
and have been generalized in the theory of Gromov hyperbolic group
Hyperbolic group
In group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
s.
von Dyck groups
Denote by D(l,m,n) the subgroupSubgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of index
Index of a subgroup
In mathematics, specifically group theory, the index of a subgroup H in a group G is the "relative size" of H in G: equivalently, the number of "copies" of H that fill up G. For example, if H has index 2 in G, then intuitively "half" of the elements of G lie in H...
2 in Δ(l,m,n) generated by words of even length in the generators. Such subgroups are sometimes referred to as "ordinary" triangle groups or von Dyck groups, after Walther von Dyck
Walther von Dyck
Walther Franz Anton von Dyck , born Dyck and later ennobled, was a German mathematician...
. For spherical, Euclidean, and hyperbolic triangles, these correspond to the elements of the group that preserve the orientation of the triangle – the group of rotations. For projective (elliptic) triangles, they cannot be so interpreted, as the projective plane is non-orientable, so there is no notion of "orientation-preserving". The reflections are however locally orientation-reversing (and every manifold is locally orientable, because locally Euclidean): they fix a line and at each point in the line are a reflection across the line.
The groups D(l,m,n) is defined by the following presentation:

In terms of the generators above, these are x = ab, y = ca, yx = cb. Geometrically, the three elements x, y, xy correspond to rotations by 2π/l, 2π/m and 2π/n about the three vertices of the triangle.
Note that D(l,m,n) ≅ D(m,l,n) ≅ D(n,m,l), so D(l,m,n) is independent of the order of the l,m,n.
A hyperbolic von Dyck group is a Fuchsian group
Fuchsian group
In mathematics, a Fuchsian group is a discrete subgroup of PSL. The group PSL can be regarded as a group of isometries of the hyperbolic plane, or conformal transformations of the unit disc, or conformal transformations of the upper half plane, so a Fuchsian group can be regarded as a group acting...
, a discrete group consisting of orientation-preserving isometries of the hyperbolic plane.
Overlapping tilings
Triangle groups preserve a tiling by triangles, namely a fundamental domainFundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
for the action (the triangle defined by the lines of reflection), called a Möbius triangle, and are given by a triple of integers, (l,m,n), – integers correspond to (2l,2m,2n) triangles coming together at a vertex. There are also tilings by overlapping triangles, which correspond to Schwarz triangle
Schwarz triangle
In geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
s with rational numbers (l/a,m/b,n/c), where the denominators are coprime
Coprime
In number theory, a branch of mathematics, two integers a and b are said to be coprime or relatively prime if the only positive integer that evenly divides both of them is 1. This is the same thing as their greatest common divisor being 1...
to the numerators. This corresponds to edges meeting at angles of aπ/l (resp.), which corresponds to a rotation of 2aπ/l (resp.), which has order l and is thus identical as an abstract group element, but distinct when represented by a reflection.
For example, the Schwartz triangle (2 3 3) yields a density
Polytope density
In geometry, polytope density represents the number of windings of a polytope, particularly a uniform or regular polytope, around its center. It can be visually determined by counting the minimum number of facet crossings of a ray from the center to infinity...
1 tiling of the sphere, while the triangle (2 3/2 3) yields a density 3 tiling of the sphere, but with the same abstract group. These symmetries of overlapping tilings are not considered triangle groups.
History
Triangle groups date at least to the presentation of the icosahedral group as the (rotational) (2,3,5) triangle group by William Rowan HamiltonWilliam Rowan Hamilton
Sir William Rowan Hamilton was an Irish physicist, astronomer, and mathematician, who made important contributions to classical mechanics, optics, and algebra. His studies of mechanical and optical systems led him to discover new mathematical concepts and techniques...
in 1856, in his paper on Icosian Calculus
Icosian Calculus
The Icosian Calculus is a non-commutative algebraic structure discovered by the Irish mathematician William Rowan Hamilton in 1856.In modern terms, he gave a group presentation of the icosahedral rotation group by generators and relations....
.
Applications
Triangle groups arise in arithmetic geometry. The modular groupModular group
In mathematics, the modular group Γ is a fundamental object of study in number theory, geometry, algebra, and many other areas of advanced mathematics...
is generated by two elements, S and T, subject to the relations S² = (ST)³ = 1 (no relation on T), is the rotational triangle group (2,3,∞) and maps onto all triangle groups (2,3,n) by adding the relation Tn = 1. More generally, the Hecke group Hq is by two elements, S and T, subject to the relations S² = (ST)q = 1 (no relation on T), is the rotational triangle group (2,q,∞), and maps onto all triangle groups (2,q,n) by adding the relation Tn = 1 the modular group is the Hecke group H3. In Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
's theory of dessins d'enfants, a Belyi function gives rise to a tessellation of a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
by reflection domains of a triangle group.
All 26 sporadic group
Sporadic group
In the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
s are quotients of triangle groups, of which 12 are Hurwitz groups (quotients of the (2,3,7) group).
See also
- Schwarz triangleSchwarz triangleIn geometry, a Schwarz triangle, named after Hermann Schwarz is a spherical triangle that can be used to tile a sphere, possibly overlapping, through reflections in its edges. They were classified in ....
- The Schwarz triangle map is a map of triangles to the upper half-plane.
- Geometric group theoryGeometric group theoryGeometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
External links
- Robert Dawson Some spherical tilings (undated, earlier than 2004) (Shows a number of interesting sphere tilings, most of which are not triangle group tilings.)
- elizabeth r chen triangle groups (2010) desktop background pictures



