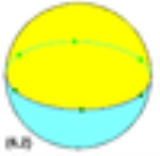
Dihedron
Encyclopedia
| Set of regular n-gonal dihedrons | |
|---|---|
 Example hexagonal dihedron on a sphere |
|
| Type | Regular polyhedron Regular polyhedron A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags... or spherical tiling |
| Faces | 2 n-gons |
| Edges | n |
| Vertices | n |
| Schläfli symbol | {n,2} |
| Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
n2 |
| Coxeter–Dynkin diagram | |
| Wythoff symbol Wythoff symbol In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles.... |
2 | n 2 |
| Symmetry group | Dnh, [2,n], (*22n) |
| Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
hosohedron |
A dihedron is a type of polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is the fundamental domain of a lens space
Lens space
A lens space is an example of a topological space, considered in mathematics. The term often refers to a specific class of 3-manifolds, but in general can be defined for higher dimensions....
L(p,q).
Usually a regular dihedron is implied (two regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s) and this gives it a Schläfli symbol as {n, 2}.
The dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of a n-gonal dihedron is the n-gonal hosohedron, where n digon
Digon
In geometry, a digon is a polygon with two sides and two vertices. It is degenerate in a Euclidean space, but may be non-degenerate in a spherical space.A digon must be regular because its two edges are the same length...
faces share two vertices.
As a polyhedron
A dihedron can be considered a degenerate prismPrism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
consisting of two (planar) n-sided polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s connected "back-to-back", so that the resulting object has no depth.
From a Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
on dihedral symmetry, a truncation
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
operation on a regular {n,2} dihedron transforms it into a 4.4.n
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
n-prism.
As a tiling on a sphere
As a spherical tiling, a dihedron can exist as nondegenerate form, with two n-sided faces covering the sphere, each face being a hemisphereSphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
, and vertices around a great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
. (It is regular if the vertices are equally spaced.)
The regular polyhedron {2,2} is self-dual, and is both a hosohedron and a dihedron.
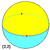
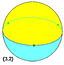
Regular dihedron examples: (spherical tilings)
 |
 |
 |
 |
Ditopes
A regular ditope is an n-dimensional analogue of a dihedron, with Schläfli symbol {p,..q,r,2}. It has two facets, {p,...,q,r}, which share all ridgesRidge (geometry)
In geometry, a ridge is an -dimensional element of an n-dimensional polytope. It is also sometimes called a subfacet for having one lower dimension than a facet.By dimension, this corresponds to:*a vertex of a polygon;...
, {p,...,q} in common.

