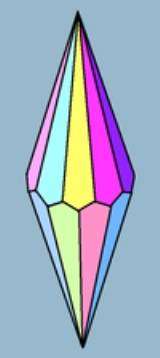
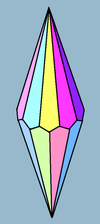
Trapezohedron
Encyclopedia
| Set of trapezohedra | |
|---|---|
 |
|
| Faces | 2n kites Kite (geometry) In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other... |
| Edges | 4n |
| Vertices | 2n+2 |
| Face configuration Face configuration In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face.... |
V3.3.3.n |
| Symmetry group | Dnd, [2+,2n], (2*n) |
| Dual polyhedron Dual polyhedron In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another... |
antiprism Antiprism In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles... |
| Properties | convex, face-transitive |
The n-gonal trapezohedron, antidipyramid or deltohedron is the dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
of an n-gonal antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
. Its 2n faces are congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
kites
Kite (geometry)
In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...
(also called trapezia in the US, trapezoids in Britain, or deltoids). The faces are symmetrically staggered.
The n-gon part of the name does not reference the faces here but arrangement of vertices around an axis of symmetry. The dual n-gonal antiprism has two actual n-gon faces.
An n-gonal trapezohedron can be decomposed into two equal n-gonal pyramids and an n-gonal antiprism
Antiprism
In geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
.
Name
These figures, sometimes called deltohedra, must not be confused with deltahedraDeltahedron
A deltahedron is a polyhedron whose faces are all equilateral triangles. The name is taken from the Greek majuscule delta , which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces...
, whose faces are equilateral triangles.
In texts describing the crystal habit
Crystal habit
Crystal habit is an overall description of the visible external shape of a mineral. This description can apply to an individual crystal or an assembly of crystals or aggregates....
s of minerals, the word trapezohedron is often used for the polyhedron properly known as a deltoidal icositetrahedron
Deltoidal icositetrahedron
In geometry, a deltoidal icositetrahedron is a Catalan solid which looks a bit like an overinflated cube. Its dual polyhedron is the rhombicuboctahedron....
.
Forms

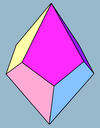


- Trigonal trapezohedronTrigonal trapezohedronIn geometry, the trigonal trapezohedron or deltohedron is the first in an infinite series of face-uniform polyhedra which are dual to the antiprisms. It has six faces which are congruent rhombi....
- 6 (rhombic) faces - dual octahedronOctahedronIn geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
- A cubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
is a special case trigonal trapezohedron with square faces - A trigonal trapezohedron is a special case rhombohedronRhombohedronIn geometry, a rhombohedron is a three-dimensional figure like a cube, except that its faces are not squares but rhombi. It is a special case of a parallelepiped where all edges are the same length....
with congruent rhombic faces
- A cube
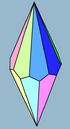
- Tetragonal trapezohedronTetragonal trapezohedronThe tetragonal trapezohedron or deltohedron is the second in an infinite series of face-uniform polyhedra which are dual to the antiprisms. It has eight faces which are congruent kites.- External links :*...
- 8 kite faces - dual square antiprismSquare antiprismIn geometry, the square antiprism is the second in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps... - Pentagonal trapezohedronPentagonal trapezohedronThe pentagonal trapezohedron or deltohedron is the third in an infinite series of face-transitive polyhedra which are dual polyhedra to the antiprisms. It has ten faces which are congruent kites....
- 10 kite faces - dual pentagonal antiprismPentagonal antiprismIn geometry, the pentagonal antiprism is the third in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps. It consists of two pentagons joined to each other by a ring of 10 triangles for a total of 12 faces... - Hexagonal trapezohedronHexagonal trapezohedronThe hexagonal trapezohedron or deltohedron is the fourth in an infinite series of face-uniform polyhedra which are dual polyhedron to the antiprisms. It has twelve faces which are congruent kites.- External links :* The Encyclopedia of Polyhedra...
- 12 kite faces - dual hexagonal antiprismHexagonal antiprismIn geometry, the hexagonal antiprism is the 4th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms... - Heptagonal trapezohedron - 14 kite faces - dual heptagonal antiprism
- Octagonal trapezohedronOctagonal trapezohedronThe octagonal trapezohedron or deltohedron is the sixth in an infinite series of face-uniform polyhedra which are dual polyhedron to the antiprisms. It has sixteen faces which are congruent kites.- External links :* The Encyclopedia of Polyhedra...
- 16 kite faces - dual octagonal antiprismOctagonal antiprismIn geometry, the octagonal antiprism is the 6th in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- See also :* Set of antiprisms... - Enneagonal trapezohedron - 18 kite faces - dual enneagonal antiprism
- Decagonal trapezohedronDecagonal trapezohedronThe decagonal trapezohedron or deltohedron is the eighth in an infinite series of face-uniform polyhedra which are dual polyhedron to the antiprisms. It has twenty faces which are congruent kites.- External links :* The Encyclopedia of Polyhedra...
- 20 kite faces - dual decagonal antiprismDecagonal antiprismIn geometry, the decagonal antiprism is the eighth in an infinite set of antiprisms formed by an even-numbered sequence of triangle sides closed by two polygon caps.If faces are all regular, it is a semiregular polyhedron.- External links :*...
- ...n-gonal trapezohedron - 2n kite faces - dual n-gonal antiprismAntiprismIn geometry, an n-sided antiprism is a polyhedron composed of two parallel copies of some particular n-sided polygon, connected by an alternating band of triangles...
- ...n-gonal trapezohedron - 2n kite faces - dual n-gonal antiprism
In the case of the dual of a regular triangular antiprism the kites are rhombi, hence these trapezohedra are also zonohedra
Zonohedron
A zonohedron is a convex polyhedron where every face is a polygon with point symmetry or, equivalently, symmetry under rotations through 180°. Any zonohedron may equivalently be described as the Minkowski sum of a set of line segments in three-dimensional space, or as the three-dimensional...
. They are called rhombohedron. They are cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
s scaled in the direction of a body diagonal. Also they are the parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
s with congruent rhombic faces.
A special case of a rhombohedron is one of the which the rhombi which form the faces have angles of 60° and 120°. It can be decomposed into two equal regular tetrahedra and a regular octahedron
Octahedron
In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
. Since parallelepipeds can fill space
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
, so can a combination of regular tetrahedra and regular octahedra
Tetrahedral-octahedral honeycomb
The tetrahedral-octahedral honeycomb or alternated cubic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed of alternating octahedra and tetrahedra in a ratio of 1:2....
.
Examples
- Crystal arrangementsCrystal systemIn crystallography, the terms crystal system, crystal family, and lattice system each refer to one of several classes of space groups, lattices, point groups, or crystals...
of atoms can repeat in space with trapezohedral cells. - The pentagonal trapezohedronPentagonal trapezohedronThe pentagonal trapezohedron or deltohedron is the third in an infinite series of face-transitive polyhedra which are dual polyhedra to the antiprisms. It has ten faces which are congruent kites....
is the only polyhedron other than the Platonic solidPlatonic solidIn geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s commonly used as a dieDiceA die is a small throwable object with multiple resting positions, used for generating random numbers...
in roleplaying games such as Dungeons and Dragons. Having 10 sides, it can be used in repetition to generate any decimal-based uniform probability desired. Two dice of different colors are typically used for the two digitNumerical digitA digit is a symbol used in combinations to represent numbers in positional numeral systems. The name "digit" comes from the fact that the 10 digits of the hands correspond to the 10 symbols of the common base 10 number system, i.e...
s to represent numbers from 00 to 99.
Symmetry
The symmetry groupSymmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
of an n-gonal trapezohedron is Dnd of order 4n, except in the case of a cube, which has the larger symmetry group Od of order 48, which has four versions of D3d as subgroups.
The rotation group
Rotation group
In mechanics and geometry, the rotation group is the group of all rotations about the origin of three-dimensional Euclidean space R3 under the operation of composition. By definition, a rotation about the origin is a linear transformation that preserves length of vectors and preserves orientation ...
is Dn of order 2n, except in the case of a cube, which has the larger rotation group O of order 24, which has four versions of D3 as subgroups.
In popular culture
- H.P. Lovecraft's short story "The Haunter of the DarkThe Haunter of the Dark"The Haunter of the Dark" is a horror story in the Cthulhu Mythos genre. It was written by H. P. Lovecraft in November 1935, and published in the December 1936 edition of Weird Tales...
" features a "crazily angled stone" of extraterrestrial origin called the "Shining Trapezohedron". - In the PlayStation 3 game Disgaea 3: Absence of JusticeDisgaea 3: Absence of Justiceis the third video game in the Disgaea series by Nippon Ichi. It was released on January 31, 2008 in Japan for the PlayStation 3 video game console. The North American version was released by NIS America on August 26, 2008...
, the most powerful emblem equipment in the game is called 'Trapezohedron' - In Final Fantasy XIIIFinal Fantasy XIIIis a console role-playing video game developed and published by Square Enix for the PlayStation 3 and the Xbox 360. Released in 2009 in Japan and 2010 in North America and PAL regions, it is the thirteenth major installment in the Final Fantasy series...
as the catalyst required to create any of the six ultimate weapons. - In the PlayStation game Wild Arms 2Wild Arms 2Wild Arms 2, known in Japan as , is a role-playing game developed by Media.Vision and published by Sony Computer Entertainment and the second installment in the Wild Arms series...
, the 'Trapezohedron' is used to imprison the Kuiper Belt but is not actually Trapezohedron shaped.
See also
- Rhombic dodecahedronRhombic dodecahedronIn geometry, the rhombic dodecahedron is a convex polyhedron with 12 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. Its dual is the cuboctahedron.-Properties:...
- Rhombic triacontahedronRhombic triacontahedronIn geometry, the rhombic triacontahedron is a convex polyhedron with 30 rhombic faces. It is an Archimedean dual solid, or a Catalan solid. It is the polyhedral dual of the icosidodecahedron, and it is a zonohedron....
- BipyramidBipyramidAn n-gonal bipyramid or dipyramid is a polyhedron formed by joining an n-gonal pyramid and its mirror image base-to-base.The referenced n-gon in the name of the bipyramids is not an external face but an internal one, existing on the primary symmetry plane which connects the two pyramid halves.The...
- Conway polyhedron notationConway polyhedron notationConway polyhedron notation is used to describe polyhedra based on a seed polyhedron modified by various operations.The seed polyhedra are the Platonic solids, represented by their first letter of their name ; the prisms , antiprisms and pyramids...
External links
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra
- VRMLVRMLVRML is a standard file format for representing 3-dimensional interactive vector graphics, designed particularly with the World Wide Web in mind...
models (George Hart) <3> <4> <5> <6> <7> http://www.georgehart.com/virtual-polyhedra/vrml/octagonal_trapezohedron.wrl<8> <9> <10> - Conway Notation for Polyhedra Try: "dAn", where n=3,4,5... example "dA5" is a pentagonal trapezohedron.
- VRML
- Paper model tetragonal (square) trapezohedron

