A deltahedron is a polyhedron

Polyhedron

In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...

 whose face

Face (geometry)

In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...

s are all equilateral triangles. The name is taken from the Greek

Greek language

Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...

 majuscule delta

Delta (letter)

Delta is the fourth letter of the Greek alphabet. In the system of Greek numerals it has a value of 4. It was derived from the Phoenician letter Dalet...

 (Δ), which has the shape of an equilateral triangle. There are infinitely many deltahedra, but of these only eight are convex, having 4, 6, 8, 10, 12, 14, 16 and 20 faces. The number of faces, edges, and vertices

Vertex (geometry)

In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...

 is listed below for each of the eight convex deltahedra.

The deltahedra should not be confused with the deltohedra (spelled with an "o"), polyhedra whose faces are geometric kite

Kite (geometry)

In Euclidean geometry a kite is a quadrilateral whose four sides can be grouped into two pairs of equal-length sides that are next to each other. In contrast, a parallelogram also has two pairs of equal-length sides, but they are opposite each other rather than next to each other...

s.

The eight convex deltahedra

There are only 8 strictly-convex deltahedra:

Name	Image	Faces	Edges	Vertices	Vertex configuration Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... s	Symmetry group Point groups in three dimensions In geometry, a point group in three dimensions is an isometry group in three dimensions that leaves the origin fixed, or correspondingly, an isometry group of a sphere. It is a subgroup of the orthogonal group O, the group of all isometries that leave the origin fixed, or correspondingly, the group...
regular tetrahedron Tetrahedron In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...		4	6	4	4 × 33
triangular dipyramid Triangular dipyramid In geometry, the triangular bipyramid is the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces....		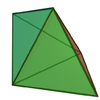6	9	5	2 × 33 3 × 34
regular octahedron Octahedron In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....		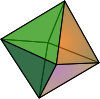8	12	6	6 × 34
pentagonal dipyramid Pentagonal dipyramid In geometry, the pentagonal bipyramid is third of the infinite set of face-transitive bipyramids.Each bipyramid is the dual of a uniform prism.If the faces are equilateral triangles, it is a deltahedron and a Johnson solid...		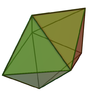10	15	7	5 × 34 2 × 35
snub disphenoid Snub disphenoid In geometry, the snub disphenoid is one of the Johnson solids . It is a three-dimensional solid that has only equilateral triangles as faces, and is therefore a deltahedron. It is not a regular polyhedron because some vertices have four faces and others have five...		12	18	8	4 × 34 4 × 35
triaugmented triangular prism Triaugmented triangular prism In geometry, the triaugmented triangular prism is one of the Johnson solids . As the name suggests, it can be constructed by attaching square pyramids to each of the three equatorial faces of the triangular prism...		14	21	9	3 × 34 6 × 35
gyroelongated square dipyramid Gyroelongated square dipyramid In geometry, the gyroelongated square bipyramid is one of the Johnson solids . As the name suggests, it can be constructed by gyroelongating an octahedron by inserting a square antiprism between its congruent halves...		16	24	10	2 × 34 8 × 35
regular icosahedron Icosahedron In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....		20	30	12	12 × 35

Three of the deltahedra are Platonic solid

Platonic solid

In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...

s (polyhedra in which a constant number of identical regular faces meet at each vertex). These are:

• the 4-faced deltahedron (or tetrahedron
  Tetrahedron
  In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
  
  ), in which three faces meet at each vertex
• the 8-faced deltahedron (or octahedron
  Octahedron
  In geometry, an octahedron is a polyhedron with eight faces. A regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex....
  
  ), in which four faces meet at each vertex
• the 20-faced deltahedron (or icosahedron
  Icosahedron
  In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
  
  ), in which five faces meet at each vertex

In the 6-faced deltahedron, some vertices have degree 3 and some degree 4. In the 10-, 12-, 14-, and 16-faced deltahedra, some vertices have degree 4 and some degree 5. These five irregular deltahedra belong to the class of Johnson solid

Johnson solid

In geometry, a Johnson solid is a strictly convex polyhedron, each face of which is a regular polygon, but which is not uniform, i.e., not a Platonic solid, Archimedean solid, prism or antiprism. There is no requirement that each face must be the same polygon, or that the same polygons join around...

s: convex polyhedra with regular polygon

Regular polygon

A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...

s for faces.

Deltahedra retain their shape, even if the edges are free to rotate around their vertices so that the angles between edges are fluid. Not all polyhedra have this property: for example, if you relax some of the angles of a cube

Cube

In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...

, the cube can be deformed into a non-right square prism

Prism (geometry)

In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...

.

Non-convex forms

There are an infinite number of nonconvex forms.

Some examples of face-intersecting deltahedra:

• Great icosahedron - a Kepler-Poinsot solid
  Kepler-Poinsot solid
  In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra. They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures....
  
  .

Other nonconvex can be generated by adding equilateral pyramids to the faces of all 5 regular polyhedra:

1. Equilateral triakis tetrahedron
   Triakis tetrahedron
   In geometry, a triakis tetrahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated tetrahedron.It can be seen as a tetrahedron with triangular pyramids added to each face; that is, it is the Kleetope of the tetrahedron...
   
   
2. Equilateral tetrakis hexahedron
   Tetrakis hexahedron
   In geometry, a tetrakis hexahedron is a Catalan solid. Its dual is the truncated octahedron, an Archimedean solid. It can be seen as a cube with square pyramids covering each square face; that is, it is the Kleetope of the cube....
   
   
3. Equilateral triakis octahedron
   Triakis octahedron
   In geometry, a triakis octahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated cube.It can be seen as an octahedron with triangular pyramids added to each face; that is, it is the Kleetope of the octahedron. It is also sometimes called a trisoctahedron, or, more...
   
    (stella octangula
   Stella octangula
   The stellated octahedron, or stella octangula, is the only stellation of the octahedron. It was named by Johannes Kepler in 1609, though it was known to earlier geometers...
   
   )
4. Equilateral pentakis dodecahedron
   Pentakis dodecahedron
   In geometry, a pentakis dodecahedron is a Catalan solid. Its dual is the truncated icosahedron, an Archimedean solid.It can be seen as a dodecahedron with a pentagonal pyramid covering each face; that is, it is the Kleetope of the dodecahedron...
   
   
5. Equilateral triakis icosahedron
   Triakis icosahedron
   In geometry, the triakis icosahedron is an Archimedean dual solid, or a Catalan solid. Its dual is the truncated dodecahedron.It can be seen as an icosahedron with triangular pyramids augmented to each face; that is, it is the Kleetope of the icosahedron...
   
   

Also by adding inverted pyramids to faces:

• Wenninger's third stellated
  Stellation
  Stellation is a process of constructing new polygons , new polyhedra in three dimensions, or, in general, new polytopes in n dimensions. The process consists of extending elements such as edges or face planes, usually in a symmetrical way, until they meet each other again...
  
   icosahedra
  Icosahedron
  In geometry, an icosahedron is a regular polyhedron with 20 identical equilateral triangular faces, 30 edges and 12 vertices. It is one of the five Platonic solids....
  
  

Great icosahedron (20 intersecting triangles)

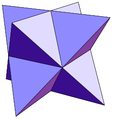stella octangula Stella octangula The stellated octahedron, or stella octangula, is the only stellation of the octahedron. It was named by Johannes Kepler in 1609, though it was known to earlier geometers... (24 triangles)

Third stellation of icosahedron (60 triangles)

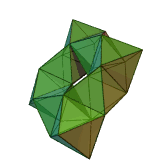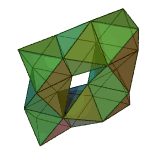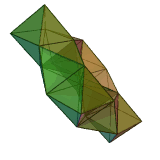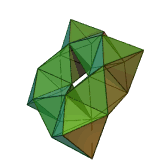A toroidal deltahedron Toroidal polyhedron In geometry, a toroidal polyhedron is a polyhedron with a genus of 1 or greater, representing topological torus surfaces.Non-self-intersecting toroidal polyhedra are embedded tori, while self-intersecting toroidal polyhedra are toroidal as abstract polyhedra, which can be verified by their Euler... (48 triangles)

External links

• Eight convex deltahedron
• Deltahedron
• Deltahedron