Stress analysis
Encyclopedia
Stress analysis is an engineering
(e.g., civil engineering
and mechanical engineering
) discipline that determines the stress in materials and structures subjected to static
or dynamic
force
s or loads. A stress analysis is required for the study and design of structures, e.g., tunnels, dams, mechanical parts, and structural frames among others, under prescribed or expected loads. Stress analysis may be applied as a design
step to structures that do not yet exist.
The aim of the analysis is usually to determine whether the element or collection of elements, usually referred to as a structure, can safely withstand the specified forces. This is achieved when the determined stress from the applied force(s) is less than the ultimate tensile strength
, ultimate compressive strength
or fatigue
strength the material is known to be able to withstand, though ordinarily a factor of safety
is applied in design.
Analysis may be performed through mathematical modelling or simulation, through experimental testing procedures, or a combination of techniques.
Engineering quantities are usually measured in megapascals (MPa) or giga
pascals (GPa). In imperial units, stress is expressed in pounds-force per square inch (psi) or kilopounds-force per square inch (ksi).
A key part of analysis involves determining the type of loads acting on a structure, including tension, compression, shear
, torsion
, bending
, or combinations of such loads. When forces are applied, or expected to be applied, repeatedly, nearly all materials will rupture or fail at a lower stress than they would otherwise. The analysis to determine stresses under these cyclic loading conditions is termed fatigue
analysis and is most often applied to aerodynamic structural systems.
for linear elastic
materials, are used to describe the stress:strain
relationship in these calculations. A boundary-value problem based on the theory of elasticity is applied to structures expected to deform elastically
, i.e. infinitesimal strains, under design loads. When the loads applied to the structure induce plastic deformations, the theory of plasticity
is implemented.
Approximate solutions for boundary-value problems can be obtained through the use of numerical methods such as the finite element method
, the finite difference method
, and the boundary element method
, which are implemented in computer programs. Analytical or close-form solutions can be obtained for simple geometries, constitutive relations, and boundary conditions.
All real objects occupy a three-dimensional space. The stress analysis can be simplified in cases where the physical dimensions and the loading conditions allows the structure to be assumed as one-dimensional or two-dimensional. For a two-dimensional analysis a plane stress or a plane strain condition can be assumed.
s. In this case the process would more properly be known as testing (destructive
or non-destructive). Experimental methods may be used in cases where mathematical approaches are cumbersome or inaccurate. Special equipment appropriate to the experimental method is used to apply the static or dynamic loading.
There are a number of experimental methods which may be used:
Tensile testing
is a fundamental materials science
test in which a sample is subjected to uniaxial tension until failure. The results from the test are commonly used to select a material for an application, for quality control
, and to predict how a material will react under other types of forces. Properties that are directly measured via a tensile test are ultimate tensile strength, maximum elongation and reduction in area. From these measurements properties such as Young's modulus
, Poisson's ratio
, yield strength, and strain-hardening characteristics can be determined.
The photoelastic method
relies on the physical phenomenon of birefringence
. Unlike the analytical methods of stress determination, photoelasticity gives a fairly accurate picture of stress distribution even around abrupt discontinuities in a material. The method serves as an important tool for determining the critical stress points in a material and is often used for determining stress concentration factors in irregular geometries. Birefringence is exhibited by certain transparent materials. A ray of light passing through a birefringent material experiences two refractive indices. This double refraction is exhibited by many optical crystals. But photoelastic materials exhibit the property of birefringence only on the application of stress, and the magnitude of the refractive indices at each point in the material is directly related to the state of stress at that point. A model component is created made of photoelastic material with similar geometry to that of the structure on which stress analysis is to be performed. This ensures that the state of the stress in the model is similar to the state of the stress in the structure.
Dynamic mechanical analysis
is a technique used to study and characterize viscoelastic materials, particularly polymers. Polymers composed of long molecular chains have unique viscoelastic properties, which combine the characteristics of elastic solids and Newtonian fluid
s. The viscoelastic property of polymer is studied by dynamic mechanical analysis where a sinusoidal force (stress) is applied to a material and the resulting displacement (strain
) is measured. For a perfectly elastic solid, the resulting strain and the stress will be perfectly in phase. For a purely viscous fluid, there will be a 90 degree phase lag of strain with respect to stress. Viscoelastic polymers have the characteristics in between where some phase lag will occur during DMA tests. Analyzers are made for both stress and strain control. In strain control, a probe is displaced and the resulting stress of the sample is measured. In stress control, a set force is applied and several other experimental conditions (temperature, frequency, or time) can be varied.
Laboratory test are usually performed on material samples in order to determine the yield strength and the ultimate strength that the material can withstand before failure. Often a separate factor of safety is applied to the yield strength and to the ultimate strength. The factor of safety on yield strength is to prevent detrimental deformations and the factor of safety on ultimate strength is to prevent collapse.
The factor of safety is used to calculate a maximum allowable stress:
"Margin of safety" or "design factor" are other ways to express the factor of safety value. .
or by numerical methods may be required. Numerical methods include direct stiffness method
which is also referred to as the finite element method
.
The object is to determine the critical stresses in each part, and compare them to the strength of the material (see strength of materials
).
For parts that have broken in service, a forensic engineering
or failure analysis
is performed to identify weakness, where broken parts are analysed for the cause or causes of failure. The method seeks to identify the weakest component in the load path. If this is the part which actually failed, then it may corroborate independent evidence of the failure. If not, then another explanation has to be sought, such as a defective part with a lower tensile strength
than it should for example.
When a structural element is subjected to tension or compression its length will tend to elongate or shorten, and its cross-sectional area changes by an amount that depends on the Poisson's ratio
of the material. In engineering applications, structural members experience small deformations and the reduction in cross-sectional area is very small and can be neglected, i.e., the cross-sectional area is assumed constant during deformation. For this case, the stress is called engineering stress or nominal stress. In some other cases, e.g., elastomer
s and plastic
materials, the change in cross-sectional area is significant, and the stress must be calculated assuming the current cross-sectional area instead of the initial cross-sectional area. This is termed true stress and is expressed as
,
where
is the nominal (engineering) strain
, and
is nominal (engineering) stress.
The relationship between true strain and engineering strain is given by
.
In uniaxial tension, true stress is then greater than nominal stress. The converse holds in compression.
A state of plane stress exists when one of the three principal 
, stresses is zero. This usually occurs in structural elements where one dimension is very small compared to the other two, i.e. the element is flat or thin. In this case, the stresses are negligible with respect to the smaller dimension as they are not able to develop within the material and are small compared to the in-plane stresses. Therefore, the face of the element is not acted by loads and the structural element can be analyzed as two-dimensional, e.g. thin-walled structures such as plates subject to in-plane loading or thin cylinders subject to pressure loading. The other three non-zero components remain constant over the thickness of the plate.
The stress tensor can then be approximated by:
Engineering
Engineering is the discipline, art, skill and profession of acquiring and applying scientific, mathematical, economic, social, and practical knowledge, in order to design and build structures, machines, devices, systems, materials and processes that safely realize improvements to the lives of...
(e.g., civil engineering
Civil engineering
Civil engineering is a professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including works like roads, bridges, canals, dams, and buildings...
and mechanical engineering
Mechanical engineering
Mechanical engineering is a discipline of engineering that applies the principles of physics and materials science for analysis, design, manufacturing, and maintenance of mechanical systems. It is the branch of engineering that involves the production and usage of heat and mechanical power for the...
) discipline that determines the stress in materials and structures subjected to static
Statics
Statics is the branch of mechanics concerned with the analysis of loads on physical systems in static equilibrium, that is, in a state where the relative positions of subsystems do not vary over time, or where components and structures are at a constant velocity...
or dynamic
Dynamics (mechanics)
In the field of physics, the study of the causes of motion and changes in motion is dynamics. In other words the study of forces and why objects are in motion. Dynamics includes the study of the effect of torques on motion...
force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
s or loads. A stress analysis is required for the study and design of structures, e.g., tunnels, dams, mechanical parts, and structural frames among others, under prescribed or expected loads. Stress analysis may be applied as a design
Design
Design as a noun informally refers to a plan or convention for the construction of an object or a system while “to design” refers to making this plan...
step to structures that do not yet exist.
The aim of the analysis is usually to determine whether the element or collection of elements, usually referred to as a structure, can safely withstand the specified forces. This is achieved when the determined stress from the applied force(s) is less than the ultimate tensile strength
Tensile strength
Ultimate tensile strength , often shortened to tensile strength or ultimate strength, is the maximum stress that a material can withstand while being stretched or pulled before necking, which is when the specimen's cross-section starts to significantly contract...
, ultimate compressive strength
Compressive strength
Compressive strength is the capacity of a material or structure to withstand axially directed pushing forces. When the limit of compressive strength is reached, materials are crushed. Concrete can be made to have high compressive strength, e.g...
or fatigue
Fatigue (material)
'In materials science, fatigue is the progressive and localized structural damage that occurs when a material is subjected to cyclic loading. The nominal maximum stress values are less than the ultimate tensile stress limit, and may be below the yield stress limit of the material.Fatigue occurs...
strength the material is known to be able to withstand, though ordinarily a factor of safety
Factor of safety
Factor of safety , also known as safety factor , is a term describing the structural capacity of a system beyond the expected loads or actual loads. Essentially, how much stronger the system is than it usually needs to be for an intended load...
is applied in design.
Analysis may be performed through mathematical modelling or simulation, through experimental testing procedures, or a combination of techniques.
Engineering quantities are usually measured in megapascals (MPa) or giga
Giga
Giga is a unit prefix in the metric system denoting a factor of billion . It has the symbol G.Giga is derived from the Greek γίγας, meaning 'giant'...
pascals (GPa). In imperial units, stress is expressed in pounds-force per square inch (psi) or kilopounds-force per square inch (ksi).
Analysis methods
The analysis of stress within a body implies the determination at each point of the body of the magnitudes of the nine stress components. In other words, it is the determination of the internal distribution of stresses.A key part of analysis involves determining the type of loads acting on a structure, including tension, compression, shear
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
, torsion
Torsion (mechanics)
In solid mechanics, torsion is the twisting of an object due to an applied torque. In sections perpendicular to the torque axis, the resultant shear stress in this section is perpendicular to the radius....
, bending
Bending
In engineering mechanics, bending characterizes the behavior of a slender structural element subjected to an external load applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically...
, or combinations of such loads. When forces are applied, or expected to be applied, repeatedly, nearly all materials will rupture or fail at a lower stress than they would otherwise. The analysis to determine stresses under these cyclic loading conditions is termed fatigue
Fatigue (material)
'In materials science, fatigue is the progressive and localized structural damage that occurs when a material is subjected to cyclic loading. The nominal maximum stress values are less than the ultimate tensile stress limit, and may be below the yield stress limit of the material.Fatigue occurs...
analysis and is most often applied to aerodynamic structural systems.
Modelling
To determine the distribution of stress in a structure it is necessary to solve a boundary-value problem by specifying the boundary conditions, i.e. displacements and/or forces on the boundary. Constitutive equations, such as e.g. Hooke's LawHooke's law
In mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
for linear elastic
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
materials, are used to describe the stress:strain
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
relationship in these calculations. A boundary-value problem based on the theory of elasticity is applied to structures expected to deform elastically
Deformation (mechanics)
Deformation in continuum mechanics is the transformation of a body from a reference configuration to a current configuration. A configuration is a set containing the positions of all particles of the body...
, i.e. infinitesimal strains, under design loads. When the loads applied to the structure induce plastic deformations, the theory of plasticity
Plasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
is implemented.
Approximate solutions for boundary-value problems can be obtained through the use of numerical methods such as the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
, the finite difference method
Finite difference method
In mathematics, finite-difference methods are numerical methods for approximating the solutions to differential equations using finite difference equations to approximate derivatives.- Derivation from Taylor's polynomial :...
, and the boundary element method
Boundary element method
The boundary element method is a numerical computational method of solving linear partial differential equations which have been formulated as integral equations . It can be applied in many areas of engineering and science including fluid mechanics, acoustics, electromagnetics, and fracture...
, which are implemented in computer programs. Analytical or close-form solutions can be obtained for simple geometries, constitutive relations, and boundary conditions.
All real objects occupy a three-dimensional space. The stress analysis can be simplified in cases where the physical dimensions and the loading conditions allows the structure to be assumed as one-dimensional or two-dimensional. For a two-dimensional analysis a plane stress or a plane strain condition can be assumed.
Experimental testing
Stress analysis can be performed experimentally by applying forces to a test element or structure and then determining the resulting stress using sensorSensor
A sensor is a device that measures a physical quantity and converts it into a signal which can be read by an observer or by an instrument. For example, a mercury-in-glass thermometer converts the measured temperature into expansion and contraction of a liquid which can be read on a calibrated...
s. In this case the process would more properly be known as testing (destructive
Destructive testing
In destructive testing, tests are carried out to the specimen's failure, in order to understand a specimen's structural performance or material behaviour under different loads...
or non-destructive). Experimental methods may be used in cases where mathematical approaches are cumbersome or inaccurate. Special equipment appropriate to the experimental method is used to apply the static or dynamic loading.
There are a number of experimental methods which may be used:
Tensile testing
Tensile testing
Tensile testing, also known as tension testing, is a fundamental materials science test in which a sample is subjected to uniaxial tension until failure. The results from the test are commonly used to select a material for an application, for quality control, and to predict how a material will...
is a fundamental materials science
Materials science
Materials science is an interdisciplinary field applying the properties of matter to various areas of science and engineering. This scientific field investigates the relationship between the structure of materials at atomic or molecular scales and their macroscopic properties. It incorporates...
test in which a sample is subjected to uniaxial tension until failure. The results from the test are commonly used to select a material for an application, for quality control
Quality control
Quality control, or QC for short, is a process by which entities review the quality of all factors involved in production. This approach places an emphasis on three aspects:...
, and to predict how a material will react under other types of forces. Properties that are directly measured via a tensile test are ultimate tensile strength, maximum elongation and reduction in area. From these measurements properties such as Young's modulus
Young's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
, Poisson's ratio
Poisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
, yield strength, and strain-hardening characteristics can be determined.
Photoelasticity
Photoelasticity is an experimental method to determine the stress distribution in a material. The method is mostly used in cases where mathematical methods become quite cumbersome. Unlike the analytical methods of stress determination, photoelasticity gives a fairly accurate picture of stress...
relies on the physical phenomenon of birefringence
Birefringence
Birefringence, or double refraction, is the decomposition of a ray of light into two rays when it passes through certain anisotropic materials, such as crystals of calcite or boron nitride. The effect was first described by the Danish scientist Rasmus Bartholin in 1669, who saw it in calcite...
. Unlike the analytical methods of stress determination, photoelasticity gives a fairly accurate picture of stress distribution even around abrupt discontinuities in a material. The method serves as an important tool for determining the critical stress points in a material and is often used for determining stress concentration factors in irregular geometries. Birefringence is exhibited by certain transparent materials. A ray of light passing through a birefringent material experiences two refractive indices. This double refraction is exhibited by many optical crystals. But photoelastic materials exhibit the property of birefringence only on the application of stress, and the magnitude of the refractive indices at each point in the material is directly related to the state of stress at that point. A model component is created made of photoelastic material with similar geometry to that of the structure on which stress analysis is to be performed. This ensures that the state of the stress in the model is similar to the state of the stress in the structure.
Dynamic mechanical analysis
Dynamic mechanical analysis
Dynamic mechanical analysis is a technique used to study and characterize materials. It is most useful for studying the viscoelastic behavior of polymers. A sinusoidal stress is applied and the strain in the material is measured, allowing one to determine the complex modulus...
is a technique used to study and characterize viscoelastic materials, particularly polymers. Polymers composed of long molecular chains have unique viscoelastic properties, which combine the characteristics of elastic solids and Newtonian fluid
Newtonian fluid
A Newtonian fluid is a fluid whose stress versus strain rate curve is linear and passes through the origin. The constant of proportionality is known as the viscosity.-Definition:...
s. The viscoelastic property of polymer is studied by dynamic mechanical analysis where a sinusoidal force (stress) is applied to a material and the resulting displacement (strain
Strain
Strain can refer to:* Strain , variants of plants, viruses or bacteria; or an inbred animal used for experimental purposes* Strain , a chemical stress of a molecule...
) is measured. For a perfectly elastic solid, the resulting strain and the stress will be perfectly in phase. For a purely viscous fluid, there will be a 90 degree phase lag of strain with respect to stress. Viscoelastic polymers have the characteristics in between where some phase lag will occur during DMA tests. Analyzers are made for both stress and strain control. In strain control, a probe is displaced and the resulting stress of the sample is measured. In stress control, a set force is applied and several other experimental conditions (temperature, frequency, or time) can be varied.
Factor of safety
The factor of safety is a design requirement for the structure based on the uncertainty in loads, material strength, and consequences of failure. In design of structures, calculated stresses are restricted to be less than a specified allowable stress, also known as working or designed stress, that is chosen as some fraction of the yield strength or of the ultimate strength of the material which the structure is made of. The ratio of the ultimate stress to the allowable stress is defined as the factor of safety.Laboratory test are usually performed on material samples in order to determine the yield strength and the ultimate strength that the material can withstand before failure. Often a separate factor of safety is applied to the yield strength and to the ultimate strength. The factor of safety on yield strength is to prevent detrimental deformations and the factor of safety on ultimate strength is to prevent collapse.
The factor of safety is used to calculate a maximum allowable stress:
"Margin of safety" or "design factor" are other ways to express the factor of safety value. .
Load transfer
The evaluation of loads and stresses within structures is directed to finding the load transfer path. Loads will be transferred by physical contact between the various component parts and within structures. The load transfer may be identified visually, or by simple logic for simple structures. For more complex structures, more complex methods such as theoretical solid mechanicsSolid mechanics
Solid mechanics is the branch of mechanics, physics, and mathematics that concerns the behavior of solid matter under external actions . It is part of a broader study known as continuum mechanics. One of the most common practical applications of solid mechanics is the Euler-Bernoulli beam equation...
or by numerical methods may be required. Numerical methods include direct stiffness method
Direct stiffness method
As one of the methods of structural analysis, the direct stiffness method , also known as the displacement method or matrix stiffness method, is particularly suited for computer-automated analysis of complex structures including the statically indeterminate type...
which is also referred to as the finite element method
Finite element method
The finite element method is a numerical technique for finding approximate solutions of partial differential equations as well as integral equations...
.
The object is to determine the critical stresses in each part, and compare them to the strength of the material (see strength of materials
Strength of materials
In materials science, the strength of a material is its ability to withstand an applied stress without failure. The applied stress may be tensile, compressive, or shear. Strength of materials is a subject which deals with loads, deformations and the forces acting on a material. A load applied to a...
).
For parts that have broken in service, a forensic engineering
Forensic engineering
Forensic engineering is the investigation of materials, products, structures or components that fail or do not operate or function as intended, causing personal injury or damage to property. The consequences of failure are dealt with by the law of product liability. The field also deals with...
or failure analysis
Failure analysis
Failure analysis is the process of collecting and analyzing data to determine the cause of a failure. It is an important discipline in many branches of manufacturing industry, such as the electronics industry, where it is a vital tool used in the development of new products and for the improvement...
is performed to identify weakness, where broken parts are analysed for the cause or causes of failure. The method seeks to identify the weakest component in the load path. If this is the part which actually failed, then it may corroborate independent evidence of the failure. If not, then another explanation has to be sought, such as a defective part with a lower tensile strength
Tensile strength
Ultimate tensile strength , often shortened to tensile strength or ultimate strength, is the maximum stress that a material can withstand while being stretched or pulled before necking, which is when the specimen's cross-section starts to significantly contract...
than it should for example.
Uniaxial stress
If two of the dimensions of the object are very large or very small compared to the others, the object may be modelled as one-dimensional. In this case the stress tensor has only one component and is indistinguishable from a scalar. One-dimensional objects include a piece of wire loaded at the ends and a metal sheet loaded on the face and viewed up close and through the cross section.When a structural element is subjected to tension or compression its length will tend to elongate or shorten, and its cross-sectional area changes by an amount that depends on the Poisson's ratio
Poisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
of the material. In engineering applications, structural members experience small deformations and the reduction in cross-sectional area is very small and can be neglected, i.e., the cross-sectional area is assumed constant during deformation. For this case, the stress is called engineering stress or nominal stress. In some other cases, e.g., elastomer
Elastomer
An elastomer is a polymer with the property of viscoelasticity , generally having notably low Young's modulus and high yield strain compared with other materials. The term, which is derived from elastic polymer, is often used interchangeably with the term rubber, although the latter is preferred...
s and plastic
Plasticity (physics)
In physics and materials science, plasticity describes the deformation of a material undergoing non-reversible changes of shape in response to applied forces. For example, a solid piece of metal being bent or pounded into a new shape displays plasticity as permanent changes occur within the...
materials, the change in cross-sectional area is significant, and the stress must be calculated assuming the current cross-sectional area instead of the initial cross-sectional area. This is termed true stress and is expressed as
,where
is the nominal (engineering) strainStrain (materials science)
In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
, and
is nominal (engineering) stress.The relationship between true strain and engineering strain is given by
.In uniaxial tension, true stress is then greater than nominal stress. The converse holds in compression.
Plane stress
, stresses is zero. This usually occurs in structural elements where one dimension is very small compared to the other two, i.e. the element is flat or thin. In this case, the stresses are negligible with respect to the smaller dimension as they are not able to develop within the material and are small compared to the in-plane stresses. Therefore, the face of the element is not acted by loads and the structural element can be analyzed as two-dimensional, e.g. thin-walled structures such as plates subject to in-plane loading or thin cylinders subject to pressure loading. The other three non-zero components remain constant over the thickness of the plate.The stress tensor can then be approximated by:
-
.
The corresponding strain tensor is:
-
in which the non-zero
term arises from the Poisson's effectPoisson's ratioPoisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
. This strain term can be temporarily removed from the stress analysis to leave only the in-plane terms, effectively reducing the analysis to two dimensions.
Plane strain
If one dimension is very large compared to the others, the principal strainStrain (materials science)In continuum mechanics, the infinitesimal strain theory, sometimes called small deformation theory, small displacement theory, or small displacement-gradient theory, deals with infinitesimal deformations of a continuum body...
in the direction of the longest dimension is constrained and can be assumed as zero, yielding a plane strain condition (Figure 7.2). In this case, though all principal stresses are non-zero, the principal stress in the direction of the longest dimension can be disregarded for calculations. Thus, allowing a two dimensional analysis of stresses, e.g. a damDamA dam is a barrier that impounds water or underground streams. Dams generally serve the primary purpose of retaining water, while other structures such as floodgates or levees are used to manage or prevent water flow into specific land regions. Hydropower and pumped-storage hydroelectricity are...
analyzed at a cross section loaded by the reservoir.
Stress transformation in plane stress and plane strain
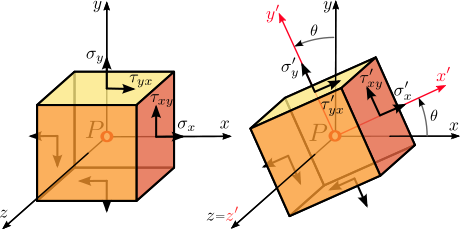
Consider a point
in a continuum under a state of plane stress, or plane strain, with stress components 
and all other stress components equal to zero (Figure 7.1, Figure 8.1). From static equilibrium of an infinitesimal material element at 
(Figure 8.2), the normal stress 
and the shear stress 
on any plane perpendicular to the 
-
plane passing through 
with a unit vector 
making an angle of 
with the horizontal, i.e. 
is the direction cosine in the 
direction, is given by:
These equations indicate that in a plane stress or plane strain condition, one can determine the stress components at a point on all directions, i.e. as a function of
, if one knows the stress components 
on any two perpendicular directions at that point. It is important to remember that we are considering a unit area of the infinitesimal element in the direction parallel to the 
-
plane.
The principal directions (Figure 8.3), i.e. orientation of the planes where the shear stress components are zero, can be obtained by making the previous equation for the shear stress
equal to zero. Thus we have:
and we obtain
This equation defines two values
which are 
apart (Figure 8.3). The same result can be obtained by finding the angle 
which makes the normal stress 
a maximum, i.e. 
The principal stresses
and 
, or minimum and maximum normal stresses 
and 
, respectively, can then be obtained by replacing both values of 
into the previous equation for 
. This can be achieved by rearranging the equations for 
and 
, first transposing the first term in the first equation and squaring both sides of each of the equations then adding them. Thus we have
where
which is the equation of a circle of radius
centered at a point with coordinates 
, called Mohr's circle. But knowing that for the principal stresses the shear stress 
, then we obtain from this equation:
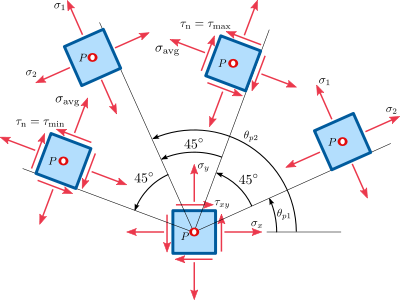
When
the infinitesimal element is oriented in the direction of the principal planes, thus the stresses acting on the rectangular element are principal stresses: 
and 
. Then the normal stress 
and shear stress 
as a function of the principal stresses can be determined by making 
. Thus we have
Then the maximum shear stress
occurs when 
, i.e. 
(Figure 8.3):
Then the minimum shear stress
occurs when 
, i.e. 
(Figure 8.3):
Graphical representation of stress at a point
Mohr's circle, Lame's stress ellipsoid (together with the stress director surface), and Cauchy's stress quadric are two-dimensional graphical representations of the state of stress at a point. They allow for the graphical determination of the magnitude of the stress tensor at a given point for all planes passing through that point. Mohr's circle is the most common graphical method.
Mohr's circle
Mohr's circle, named after Christian Otto MohrOtto MohrChristian Otto Mohr was a German civil engineer.-Biography:He was born on October 8, 1835 to a landowning family in Wesselburen in the Holstein region...
, is the locus of points that represent the state of stress on individual planes at all their orientations. The abscissaAbscissaIn mathematics, abscissa refers to that element of an ordered pair which is plotted on the horizontal axis of a two-dimensional Cartesian coordinate system, as opposed to the ordinate...
,
, and ordinateOrdinateIn mathematics, ordinate refers to that element of an ordered pair which is plotted on the vertical axis of a two-dimensional Cartesian coordinate system, as opposed to the abscissa...
,
, of each point on the circleCircleA circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
are the normal stress and shear stress components, respectively, acting on a particular cut plane with a unit vector
with components 
.
Lame's stress ellipsoid
The surface of the ellipsoid represents the locus of the endpoints of all stress vectors acting on all planes passing through a given point in the continuum body. In other words, the endpoints of all stress vectors at a given point in the continuum body lie on the stress ellipsoid surface, i.e., the radius-vector from the center of the ellipsoid, located at the material point in consideration, to a point on the surface of the ellipsoid is equal to the stress vector on some plane passing through the point. In two dimensions, the surface is represented by an ellipseEllipseIn geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
(Figure coming).
Cauchy's stress quadric
The Cauchy's stress quadric, also called the stress surface, is a surface of the second order that traces the variation of the normal stress vector
as the orientation of the planes passing through a given point is changed.
Graphical representation of the stress field
The complete state of stress in a body at a particular deformed configuration, i.e., at a particular time during the motion of the body, implies knowing the six independent components of the stress tensor
, or the three principal stresses 
, at each material point in the body at that time. However, numerical analysis and analytical methods allow only for the calculation of the stress tensor at a certain number of discrete material points. To graphically represent in two dimensions this partial picture of the stress field different sets of contour lines can be used:
- Isobars are curves along which the principal stress, e.g.,
is constant. - Isochromatics are curves along which the maximum shear stress is constant. This curves are directly determined using photoelasticity methods.
- Isopachs are curves along which the mean normal stress is constant
- Isostatics or stress trajectories are a system of curves which are at each material point tangent to the principal axes of stress.
- Isoclinics are curves on which the principal axes make a constant angle with a given fixed reference direction. These curves can also be obtained directly by photoelasticity methods.
- Slip lines are curves on which the shear stress is a maximum.
See also
- Forensic engineeringForensic engineeringForensic engineering is the investigation of materials, products, structures or components that fail or do not operate or function as intended, causing personal injury or damage to property. The consequences of failure are dealt with by the law of product liability. The field also deals with...
- Structural analysisStructural analysisStructural analysis is the determination of the effects of loads on physical structures and their components. Structures subject to this type of analysis include all that must withstand loads, such as buildings, bridges, vehicles, machinery, furniture, attire, soil strata, prostheses and...
- StressStress (physics)In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
- PipingPipingWithin industry, piping is a system of pipes used to convey fluids from one location to another. The engineering discipline of piping design studies the efficient transport of fluid....
- Worst Case Circuit AnalysisWorst case circuit analysisWorst-case circuit analysis is a cost-effective means of screening a design to ensure with a high degree of confidence that potential defects and deficiencies are identified and eliminated PRIOR TO and DURING test, production, and delivery....
- List of finite element software packages
- Isobars are curves along which the principal stress, e.g.,
-