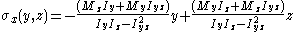Bending
Encyclopedia
In engineering mechanics, bending (also known as flexure) characterizes the behavior of a slender structural element subjected to an external load
applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically 1/10 or less, of the other two. When the length is considerably longer than the width and the thickness, the element is called a beam
. A closet
rod sagging
under the weight of clothes on clothes hanger
s is an example of a beam experiencing bending. On the other hand, a shell is a structure of any geometric form where the length and the width are of the same order of magnitude but the thickness of the structure (known as the
'wall') is considerably smaller. A large diameter, but thin-walled, short tube supported at its ends and loaded laterally is an example of a shell experiencing bending.
In the absence of a qualifier, the term bending is ambiguous because bending can occur locally in all objects. To make the usage of the term more precise, engineers refer to the bending of rods, the bending of beams, the bending of plates
, the bending of shells and so on.
and the stresses that develop are assumed not to change over time. In a horizontal beam supported at the ends and loaded downwards in the middle, the material at the over-side of the beam is compressed while the material at the underside is stretched. There are two forms of internal stresses caused by lateral loads:
These last two forces form a couple
or moment
as they are equal in magnitude and opposite in direction. This bending moment
resists the sagging deformation characteristic of a beam experiencing bending. The stress distribution in a beam can be predicted quite accurately even when some simplifying assumptions are used.
of slender beams, a major assumption is that 'plane sections remain plane'. In other words, any deformation due to shear across the section is not accounted for (no shear deformation). Also, this linear distribution is only applicable if the maximum stress is less than the yield stress of the material. For stresses that exceed yield, refer to article plastic bending
. At yield, the maximum stress experienced in the section (at the furthest points from the neutral axis of the beam) is defined as the flexural strength
.
The Euler-Bernoulli equation for the quasistatic bending of slender, isotropic, homogeneous beams of constant cross-section under an applied transverse load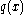 is
is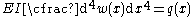
where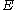 is the Young's modulus
is the Young's modulus
,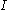 is the area moment of inertia of the cross-section, and
is the area moment of inertia of the cross-section, and 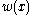 is the deflection of the neutral axis of the beam.
is the deflection of the neutral axis of the beam.
After a solution for the displacement of the beam has been obtained, the bending moment (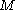 ) and shear force (
) and shear force ( ) in the beam can be calculated using the relations
) in the beam can be calculated using the relations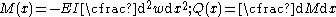
Simple beam bending is often analyzed with the Euler-Bernoulli beam equation. The conditions for using simple bending theory are :
Compressive and tensile forces develop in the direction of the beam axis under bending loads. These forces induce stresses
on the beam. The maximum compressive stress is found at the uppermost edge of the beam while the maximum tensile stress is located at the lower edge of the beam. Since the stresses between these two opposing maxima vary linear
ly, there therefore exists a point on the linear path between them where there is no bending stress. The locus
of these points is the neutral axis. Because of this area with no stress and the adjacent areas with low stress, using uniform cross section beams in bending is not a particularly efficient means of supporting a load as it does not use the full capacity of the beam until it is on the brink of collapse. Wide-flange beams (-beam
s) and truss
girder
s effectively address this inefficiency as they minimize the amount of material in this under-stressed region.
The classic formula for determining the bending stress in a beam under simple bending is:
where
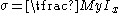 is valid only when the stress at the extreme fiber (i.e. the portion of the beam farthest from the neutral axis) is below the yield stress
is valid only when the stress at the extreme fiber (i.e. the portion of the beam farthest from the neutral axis) is below the yield stress
of the material from which it is constructed. At higher loadings the stress distribution becomes non-linear, and ductile materials will eventually enter a plastic hinge state where the magnitude of the stress is equal to the yield stress everywhere in the beam, with a discontinuity at the neutral axis where the stress changes from tensile to compressive. This plastic hinge state is typically used as a limit state in the design of steel structures.
where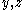 are the coordinates of a point on the cross section at which the stress is to be determined as shown to the right,
are the coordinates of a point on the cross section at which the stress is to be determined as shown to the right, 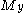 and
and 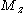 are the bending moments about the y and z centroid
are the bending moments about the y and z centroid
axes,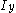 and
and 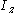 are the second moments of area (distinct from moments of inertia) about the y and z axes, and
are the second moments of area (distinct from moments of inertia) about the y and z axes, and 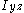 is the product of moments of area. Using this equation it is possible to calculate the bending stress at any point on the beam cross section regardless of moment orientation or cross-sectional shape. Note that
is the product of moments of area. Using this equation it is possible to calculate the bending stress at any point on the beam cross section regardless of moment orientation or cross-sectional shape. Note that  do not change from one point to another on the cross section.
do not change from one point to another on the cross section.
Large bending considerations should be implemented when the bending radius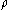 is smaller than ten section heights h:
is smaller than ten section heights h:
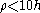
With those assumptions the stress in large bending is calculated as:
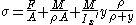
where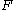 is the normal force
is the normal force
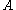 is the section area
is the section area
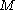 is the bending moment
is the bending moment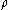 is the local bending radius (the radius of bending at the current section)
is the local bending radius (the radius of bending at the current section)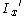 is the area moment of inertia along the x axis, at the
is the area moment of inertia along the x axis, at the 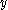 place (see Steiner's theorem
place (see Steiner's theorem
)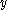 is the position along y axis on the section area in which the stress
is the position along y axis on the section area in which the stress  is calculated
is calculated
When bending radius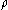 approaches infinity and y<<
approaches infinity and y<< , the original formula is back:
, the original formula is back: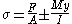 .
.
However, normals to the axis are not required to remain perpendicular to the axis after deformation.
The equation for the quasistatic bending of a linear elastic, isotropic, homogeneous beam of constant cross-section beam under these assumptions is
where is the area moment of inertia of the cross-section,
is the area moment of inertia of the cross-section, 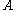 is the cross-sectional area,
is the cross-sectional area, 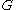 is the shear modulus, and
is the shear modulus, and  is a shear correction factor. For materials with Poisson's ratio
is a shear correction factor. For materials with Poisson's ratio
s ( ) close to 0.3, the shear correction factor for a rectangular cross-section is approximately
) close to 0.3, the shear correction factor for a rectangular cross-section is approximately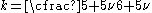
The rotation (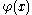 ) of the normal is described by the equation
) of the normal is described by the equation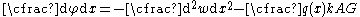
The bending moment (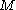 ) and the shear force (
) and the shear force (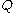 ) are given by
) are given by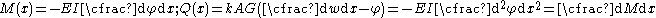
in the late 18th century. Bernoulli's equation of motion of a vibrating beam tended to overestimate the natural frequencies of beams and was improved marginally by Rayleigh
in 1877 by the addition of a mid-plane rotation. In 1921 Stephen Timoshenko
improved the theory further by incorporating the effect of shear on the dynamic response of bending beams. This allowed the theory to be used for problems involving high frequencies of vibration where the dynamic Euler-Bernoulli theory is inadequate. The Euler-Bernoulli and Timoshenko theories for the dynamic bending of beams continue to be used widely by engineers.
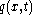 is
is
where is the Young's modulus,
is the Young's modulus, 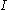 is the area moment of inertia of the cross-section,
is the area moment of inertia of the cross-section, 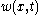 is the deflection of the neutral axis of the beam, and
is the deflection of the neutral axis of the beam, and 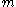 is mass per unit length of the beam.
is mass per unit length of the beam.
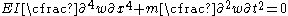
Free, harmonic vibrations of the beam can then be expressed as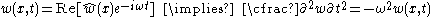
and the bending equation can be written as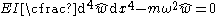
The general solution of the above equation is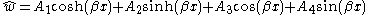
where are constants and
are constants and
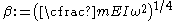
The equation for the bending of a linear elastic, isotropic, homogeneous beam of constant cross-section beam under these assumptions is
where is the polar moment of inertia
is the polar moment of inertia
of the cross-section,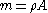 is the mass per unit length of the beam,
is the mass per unit length of the beam, 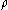 is the density of the beam,
is the density of the beam,  is the cross-sectional area,
is the cross-sectional area, 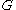 is the shear modulus, and
is the shear modulus, and 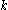 is a shear correction factor. For materials with Poisson's ratios (
is a shear correction factor. For materials with Poisson's ratios ( ) close to 0.3, the shear correction factor are approximately
) close to 0.3, the shear correction factor are approximately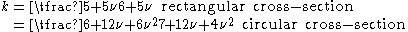
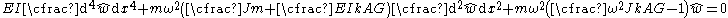
This equation can be solved by noting that all the derivatives of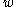 must have the same form to cancel out and hence as solution of the form
must have the same form to cancel out and hence as solution of the form 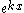 may be expected. This observation leads to the characteristic equation
may be expected. This observation leads to the characteristic equation
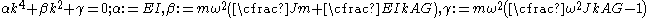
The solutions of this quartic equation are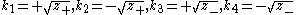
where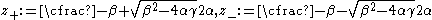
The general solution of the Timoshenko-Rayleigh beam equation for free vibrations can then be written as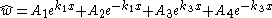
These assumptions imply that
where is the displacement of a point in the plate and
is the displacement of a point in the plate and 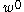 is the displacement of the mid-surface.
is the displacement of the mid-surface.
The strain-displacement relations are
The equilibrium equations are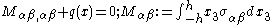
where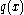 is an applied load normal to the surface of the plate.
is an applied load normal to the surface of the plate.
In terms of displacements, the equilibrium equations for an isotropic, linear elastic plate in the absence of external load can be written as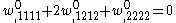
In direct tensor notation,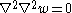
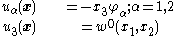
where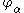 are the rotations of the normal.
are the rotations of the normal.
The strain-displacement relations that result from these assumptions are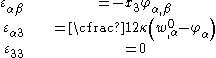
where is a shear correction factor.
is a shear correction factor.
The equilibrium equations are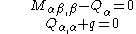
where
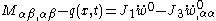
where, for a plate with density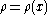 ,
,
and
The figures below show some vibrational modes of a circular plate.
Structural load
Structural loads or actions are forces, deformations or accelerations applied to a structure or its components.Loads cause stresses, deformations and displacements in structures. Assessment of their effects is carried out by the methods of structural analysis...
applied perpendicularly to a longitudinal axis of the element. The structural element is assumed to be such that at least one of its dimensions is a small fraction, typically 1/10 or less, of the other two. When the length is considerably longer than the width and the thickness, the element is called a beam
Beam (structure)
A beam is a horizontal structural element that is capable of withstanding load primarily by resisting bending. The bending force induced into the material of the beam as a result of the external loads, own weight, span and external reactions to these loads is called a bending moment.- Overview...
. A closet
Closet
A closet is a small and enclosed space, a cabinet, or a cupboard in a house or building used for general storage or hanging clothes. A closet for food storage is usually referred to as a pantry...
rod sagging
Deflection
Deflection or deflexion may refer to:* Deflection , the displacement of a structural element under load* Deflection , a technique of shooting ahead of a moving target so that the target and projectile will collide...
under the weight of clothes on clothes hanger
Clothes hanger
A clothes hanger, coat hanger or coathanger, is a device in the shape of:* Human shoulders designed to facilitate the hanging of a coat, jacket, sweater, shirt, blouse or dress in a manner that prevents wrinkles, with a lower bar for the hanging of trousers or skirts.* Clamp for the hanging of...
s is an example of a beam experiencing bending. On the other hand, a shell is a structure of any geometric form where the length and the width are of the same order of magnitude but the thickness of the structure (known as the
'wall') is considerably smaller. A large diameter, but thin-walled, short tube supported at its ends and loaded laterally is an example of a shell experiencing bending.
In the absence of a qualifier, the term bending is ambiguous because bending can occur locally in all objects. To make the usage of the term more precise, engineers refer to the bending of rods, the bending of beams, the bending of plates
Bending of plates
Bending of plates or plate bending refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the...
, the bending of shells and so on.
Quasistatic bending of beams
A beam deforms and stresses develop inside it when a transverse load is applied on it. In the quasistatic case, the amount of bending deflectionDeflection (engineering)
In engineering, deflection is the degree to which a structural element is displaced under a load. It may refer to an angle or a distance.The deflection distance of a member under a load is directly related to the slope of the deflected shape of the member under that load and can be calculated by...
and the stresses that develop are assumed not to change over time. In a horizontal beam supported at the ends and loaded downwards in the middle, the material at the over-side of the beam is compressed while the material at the underside is stretched. There are two forms of internal stresses caused by lateral loads:
- Shear stressShear stressA shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
parallel to the lateral loading plus complementary shear stress on planes perpendicular to the load direction; - Direct compressive stress in the upper region of the beam, and direct tensile stress in the lower region of the beam.
These last two forces form a couple
Couple (mechanics)
In mechanics, a couple is a system of forces with a resultant moment but no resultant force. Another term for a couple is a pure moment. Its effect is to create rotation without translation, or more generally without any acceleration of the centre of mass.The resultant moment of a couple is called...
or moment
Moment (physics)
In physics, the term moment can refer to many different concepts:*Moment of force is the tendency of a force to twist or rotate an object; see the article torque for details. This is an important, basic concept in engineering and physics. A moment is valued mathematically as the product of the...
as they are equal in magnitude and opposite in direction. This bending moment
Bending Moment
A bending moment exists in a structural element when a moment is applied to the element so that the element bends. Moments and torques are measured as a force multiplied by a distance so they have as unit newton-metres , or pound-foot or foot-pound...
resists the sagging deformation characteristic of a beam experiencing bending. The stress distribution in a beam can be predicted quite accurately even when some simplifying assumptions are used.
Euler-Bernoulli bending theory
In the Euler-Bernoulli theoryEuler-Bernoulli beam equation
Euler–Bernoulli beam theory is a simplification of the linear theory of elasticity which provides a means of calculating the load-carrying and deflection characteristics of beams. It covers the case for small deflections of a beam which is subjected to lateral loads only...
of slender beams, a major assumption is that 'plane sections remain plane'. In other words, any deformation due to shear across the section is not accounted for (no shear deformation). Also, this linear distribution is only applicable if the maximum stress is less than the yield stress of the material. For stresses that exceed yield, refer to article plastic bending
Plastic bending
Plastic bending is a nonlinear behaviour peculiar to members made of ductile materials that frequently achievemuch greater ultimate bending strength than indicated by a linear elastic bending analysis. In both the plastic and...
. At yield, the maximum stress experienced in the section (at the furthest points from the neutral axis of the beam) is defined as the flexural strength
Flexural strength
Flexural strength, also known as modulus of rupture, bend strength, or fracture strength, a mechanical parameter for brittle material, is defined as a material's ability to resist deformation under load...
.
The Euler-Bernoulli equation for the quasistatic bending of slender, isotropic, homogeneous beams of constant cross-section under an applied transverse load
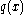 is
is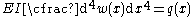
where
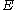 is the Young's modulus
is the Young's modulusYoung's modulus
Young's modulus is a measure of the stiffness of an elastic material and is a quantity used to characterize materials. It is defined as the ratio of the uniaxial stress over the uniaxial strain in the range of stress in which Hooke's Law holds. In solid mechanics, the slope of the stress-strain...
,
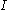 is the area moment of inertia of the cross-section, and
is the area moment of inertia of the cross-section, and 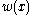 is the deflection of the neutral axis of the beam.
is the deflection of the neutral axis of the beam.After a solution for the displacement of the beam has been obtained, the bending moment (
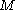 ) and shear force (
) and shear force ( ) in the beam can be calculated using the relations
) in the beam can be calculated using the relations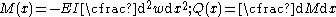
Simple beam bending is often analyzed with the Euler-Bernoulli beam equation. The conditions for using simple bending theory are :
- The beam is subject to pure bendingPure bendingPure bending is a condition of stress where a bending moment is applied to a beam without the simultaneous application of axial, shear, or torsional forces....
. This means that the shear force is zero, and that no torsional or axial loads are present. - The material is isotropic and homogeneousHomogeneous spaceIn mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
. - The material obeys Hooke's lawHooke's lawIn mechanics, and physics, Hooke's law of elasticity is an approximation that states that the extension of a spring is in direct proportion with the load applied to it. Many materials obey this law as long as the load does not exceed the material's elastic limit. Materials for which Hooke's law...
(it is linearly elastic and will not deform plastically). - The beam is initially straight with a cross section that is constant throughout the beam length.
- The beam has an axis of symmetry in the plane of bending.
- The proportions of the beam are such that it would fail by bending rather than by crushing, wrinkling or sideways bucklingBucklingIn science, buckling is a mathematical instability, leading to a failure mode.Theoretically, buckling is caused by a bifurcation in the solution to the equations of static equilibrium...
. - Cross-sections of the beam remain plane during bending.
Compressive and tensile forces develop in the direction of the beam axis under bending loads. These forces induce stresses
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
on the beam. The maximum compressive stress is found at the uppermost edge of the beam while the maximum tensile stress is located at the lower edge of the beam. Since the stresses between these two opposing maxima vary linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
ly, there therefore exists a point on the linear path between them where there is no bending stress. The locus
Locus (mathematics)
In geometry, a locus is a collection of points which share a property. For example a circle may be defined as the locus of points in a plane at a fixed distance from a given point....
of these points is the neutral axis. Because of this area with no stress and the adjacent areas with low stress, using uniform cross section beams in bending is not a particularly efficient means of supporting a load as it does not use the full capacity of the beam until it is on the brink of collapse. Wide-flange beams (-beam
I-beam
-beams, also known as H-beams, W-beams , rolled steel joist , or double-T are beams with an - or H-shaped cross-section. The horizontal elements of the "" are flanges, while the vertical element is the web...
s) and truss
Truss
In architecture and structural engineering, a truss is a structure comprising one or more triangular units constructed with straight members whose ends are connected at joints referred to as nodes. External forces and reactions to those forces are considered to act only at the nodes and result in...
girder
Girder
A girder is a support beam used in construction. Girders often have an I-beam cross section for strength, but may also have a box shape, Z shape or other forms. Girder is the term used to denote the main horizontal support of a structure which supports smaller beams...
s effectively address this inefficiency as they minimize the amount of material in this under-stressed region.
The classic formula for determining the bending stress in a beam under simple bending is:

where
 is the bending stress
is the bending stress- M - the moment about the neutral axisNeutral axisThe neutral axis is an axis in the cross section of a beam or shaft along which there are no longitudinal stresses or strains. If the section is symmetric, isotropic and is not curved before a bend occurs, then the neutral axis is at the geometric centroid...
- y - the perpendicular distance to the neutral axis
- Ix - the second moment of areaSecond moment of areaThe second moment of area, also known as the area moment of inertia, moment of inertia of plane area, or second moment of inertia is a property of a cross section that can be used to predict the resistance of beams to bending and deflection, around an axis that lies in the cross-sectional plane...
about the neutral axis x
Plastic bending
The equation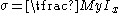 is valid only when the stress at the extreme fiber (i.e. the portion of the beam farthest from the neutral axis) is below the yield stress
is valid only when the stress at the extreme fiber (i.e. the portion of the beam farthest from the neutral axis) is below the yield stressYield (engineering)
The yield strength or yield point of a material is defined in engineering and materials science as the stress at which a material begins to deform plastically. Prior to the yield point the material will deform elastically and will return to its original shape when the applied stress is removed...
of the material from which it is constructed. At higher loadings the stress distribution becomes non-linear, and ductile materials will eventually enter a plastic hinge state where the magnitude of the stress is equal to the yield stress everywhere in the beam, with a discontinuity at the neutral axis where the stress changes from tensile to compressive. This plastic hinge state is typically used as a limit state in the design of steel structures.
Complex or asymmetrical bending
The equation above is only valid if the cross-section is symmetrical. For homogeneous beams with asymmetrical sections, the axial stress in the beam is given bywhere
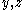 are the coordinates of a point on the cross section at which the stress is to be determined as shown to the right,
are the coordinates of a point on the cross section at which the stress is to be determined as shown to the right, 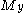 and
and 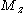 are the bending moments about the y and z centroid
are the bending moments about the y and z centroidCentroid
In geometry, the centroid, geometric center, or barycenter of a plane figure or two-dimensional shape X is the intersection of all straight lines that divide X into two parts of equal moment about the line. Informally, it is the "average" of all points of X...
axes,
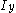 and
and 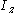 are the second moments of area (distinct from moments of inertia) about the y and z axes, and
are the second moments of area (distinct from moments of inertia) about the y and z axes, and 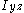 is the product of moments of area. Using this equation it is possible to calculate the bending stress at any point on the beam cross section regardless of moment orientation or cross-sectional shape. Note that
is the product of moments of area. Using this equation it is possible to calculate the bending stress at any point on the beam cross section regardless of moment orientation or cross-sectional shape. Note that  do not change from one point to another on the cross section.
do not change from one point to another on the cross section.Large bending deformation
For large deformations of the body, the stress in the cross-section is calculated using an extended version of this formula. First the following assumptions must be made:- Assumption of flat sections - before and after deformation the considered section of body remains flat (i.e. is not swirled).
- Shear and normal stresses in this section that are perpendicular to the normal vector of cross section have no influence on normal stresses that are parallel to this section.
Large bending considerations should be implemented when the bending radius
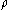 is smaller than ten section heights h:
is smaller than ten section heights h: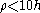
With those assumptions the stress in large bending is calculated as:
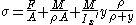
where
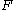 is the normal force
is the normal forceForce
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
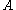 is the section area
is the section areaArea
Area is a quantity that expresses the extent of a two-dimensional surface or shape in the plane. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat...
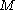 is the bending moment
is the bending moment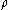 is the local bending radius (the radius of bending at the current section)
is the local bending radius (the radius of bending at the current section)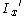 is the area moment of inertia along the x axis, at the
is the area moment of inertia along the x axis, at the 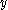 place (see Steiner's theorem
place (see Steiner's theoremParallel axis theorem
In physics, the parallel axis theorem or Huygens-Steiner theorem can be used to determine the second moment of area or the mass moment of inertia of a rigid body about any axis, given the body's moment of inertia about a parallel axis through the object's centre of mass and the perpendicular...
)
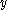 is the position along y axis on the section area in which the stress
is the position along y axis on the section area in which the stress  is calculated
is calculatedWhen bending radius
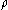 approaches infinity and y<<
approaches infinity and y<< , the original formula is back:
, the original formula is back: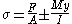 .
.Timoshenko bending theory
In 1921, Timoshenko improved upon the Euler-Bernoulli theory of beams by adding the effect of shear into the beam equation. The kinematic assumptions of the Timoshenko theory are- normals to the axis of the beam remain straight after deformation
- there is no change in beam thickness after deformation
However, normals to the axis are not required to remain perpendicular to the axis after deformation.
The equation for the quasistatic bending of a linear elastic, isotropic, homogeneous beam of constant cross-section beam under these assumptions is

where
 is the area moment of inertia of the cross-section,
is the area moment of inertia of the cross-section, 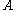 is the cross-sectional area,
is the cross-sectional area, 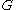 is the shear modulus, and
is the shear modulus, and  is a shear correction factor. For materials with Poisson's ratio
is a shear correction factor. For materials with Poisson's ratioPoisson's ratio
Poisson's ratio , named after Siméon Poisson, is the ratio, when a sample object is stretched, of the contraction or transverse strain , to the extension or axial strain ....
s (
 ) close to 0.3, the shear correction factor for a rectangular cross-section is approximately
) close to 0.3, the shear correction factor for a rectangular cross-section is approximately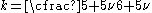
The rotation (
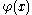 ) of the normal is described by the equation
) of the normal is described by the equation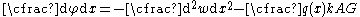
The bending moment (
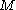 ) and the shear force (
) and the shear force (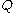 ) are given by
) are given by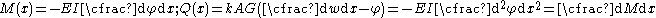
Dynamic bending of beams
The dynamic bending of beams, also known as flexural vibrations of beams, was first investigated by Daniel BernoulliDaniel Bernoulli
Daniel Bernoulli was a Dutch-Swiss mathematician and was one of the many prominent mathematicians in the Bernoulli family. He is particularly remembered for his applications of mathematics to mechanics, especially fluid mechanics, and for his pioneering work in probability and statistics...
in the late 18th century. Bernoulli's equation of motion of a vibrating beam tended to overestimate the natural frequencies of beams and was improved marginally by Rayleigh
Rayleigh
Rayleigh may refer to:*Rayleigh scattering*Rayleigh–Jeans law*Rayleigh waves*Rayleigh , named after the son of Lord Rayleigh*Rayleigh criterion in angular resolution*Rayleigh distribution*Rayleigh fading...
in 1877 by the addition of a mid-plane rotation. In 1921 Stephen Timoshenko
Stephen Timoshenko
Stanford University:* Bergman, E. O., * Kurzweil, A. C., * , * Huang, Y. S., * Wang, T. K., * Weber, H. S., * , * , * , -Publications:...
improved the theory further by incorporating the effect of shear on the dynamic response of bending beams. This allowed the theory to be used for problems involving high frequencies of vibration where the dynamic Euler-Bernoulli theory is inadequate. The Euler-Bernoulli and Timoshenko theories for the dynamic bending of beams continue to be used widely by engineers.
Euler-Bernoulli theory
The Euler-Bernoulli equation for the dynamic bending of slender, isotropic, homogeneous beams of constant cross-section under an applied transverse load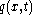 is
is
where
 is the Young's modulus,
is the Young's modulus, 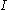 is the area moment of inertia of the cross-section,
is the area moment of inertia of the cross-section, 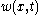 is the deflection of the neutral axis of the beam, and
is the deflection of the neutral axis of the beam, and 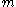 is mass per unit length of the beam.
is mass per unit length of the beam.Free vibrations
For the situation where there is no transverse load on the beam, the bending equation takes the form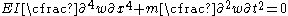
Free, harmonic vibrations of the beam can then be expressed as
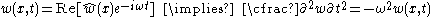
and the bending equation can be written as
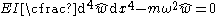
The general solution of the above equation is
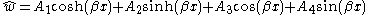
where
 are constants and
are constants and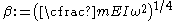
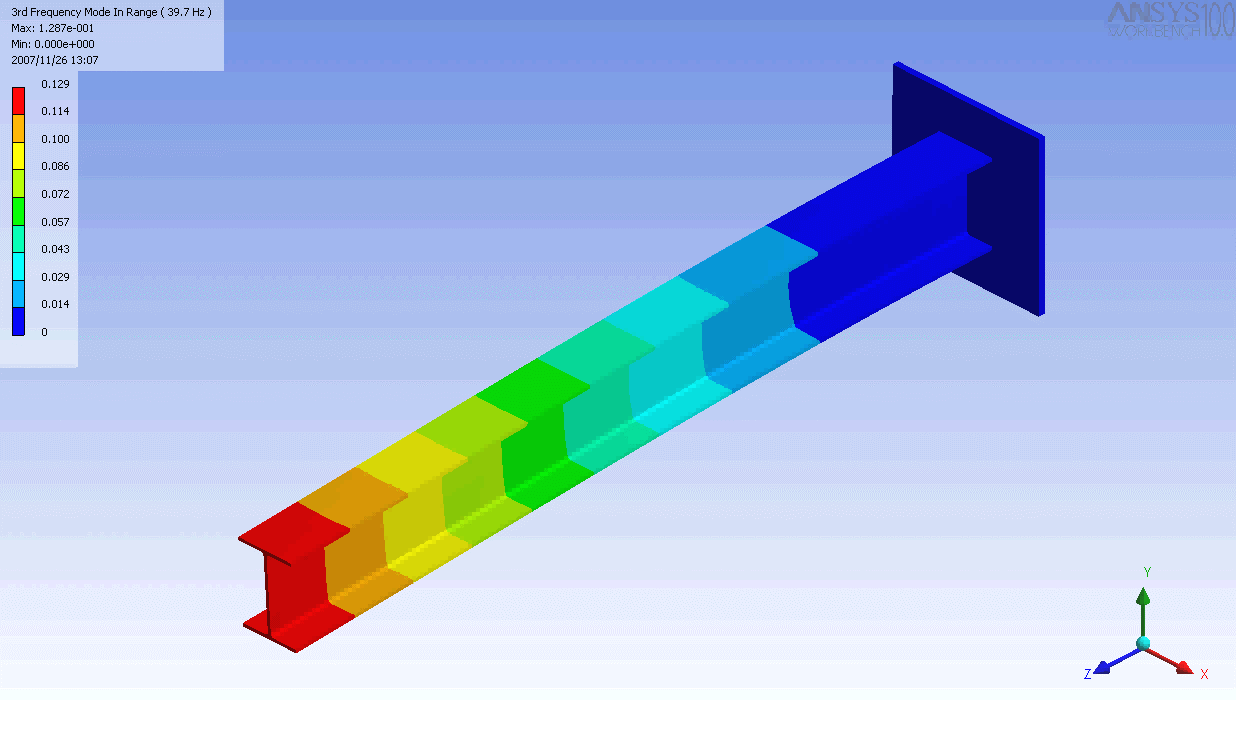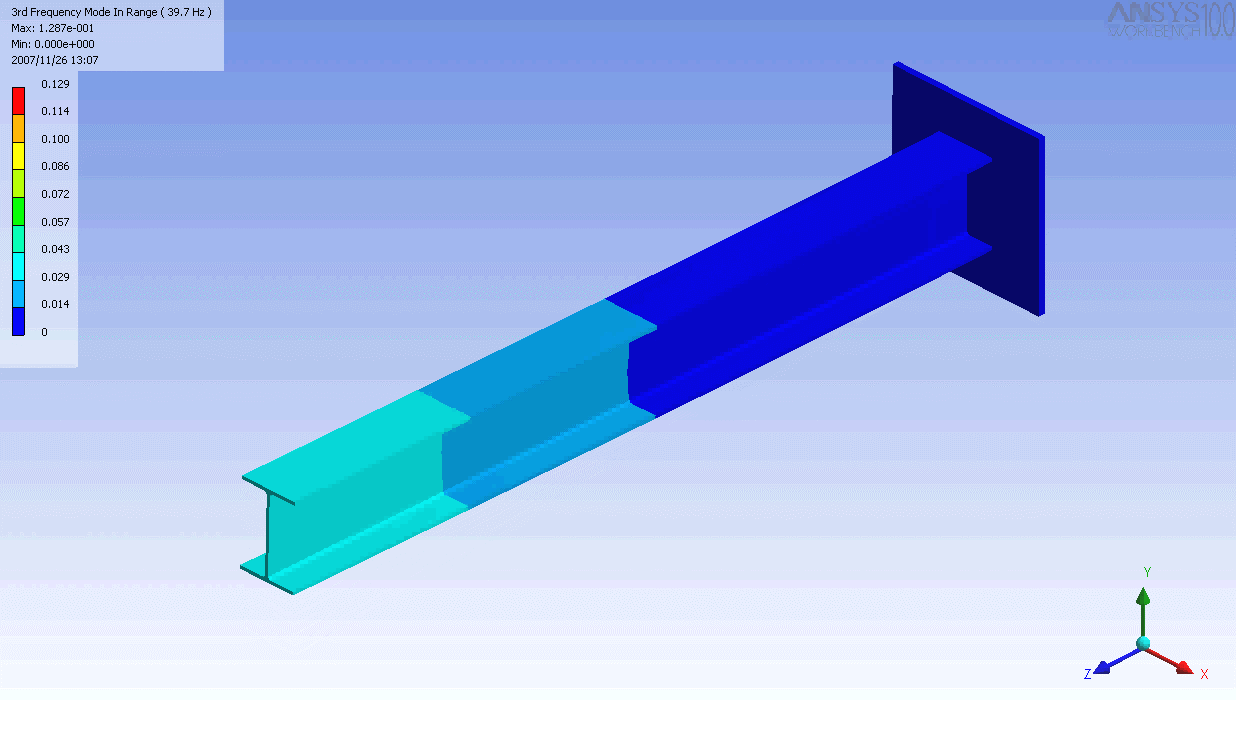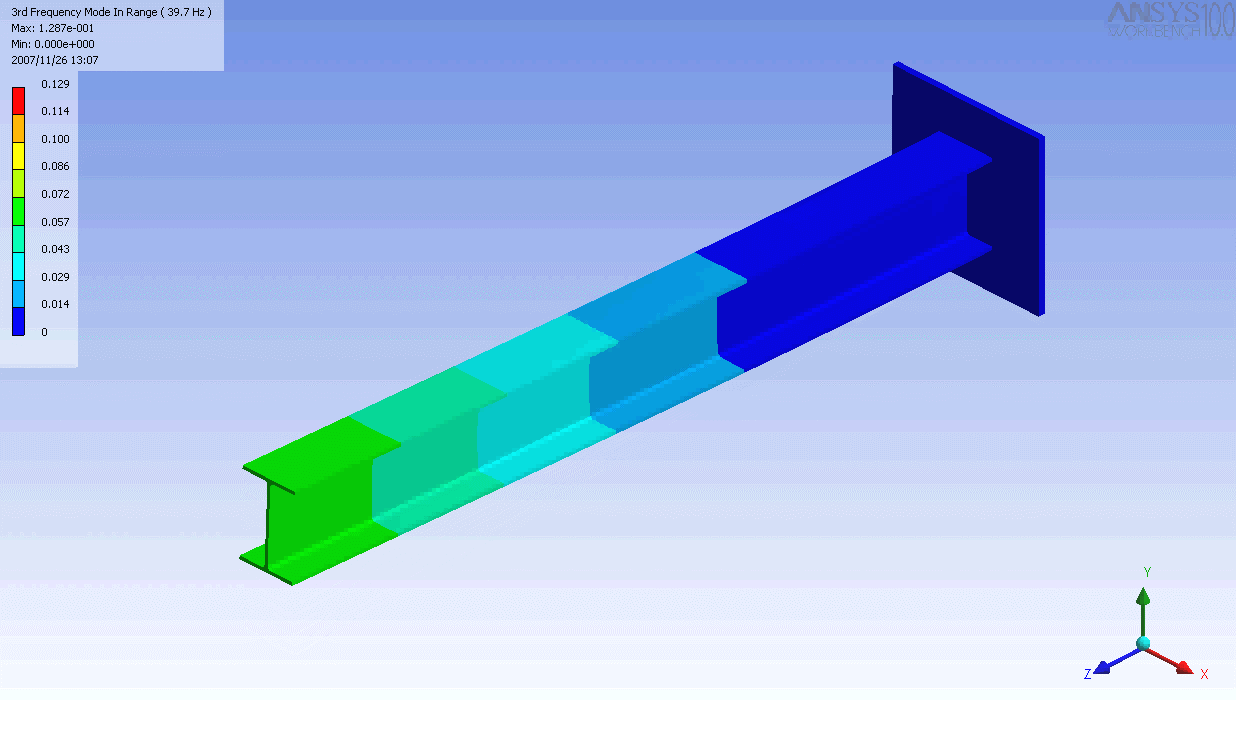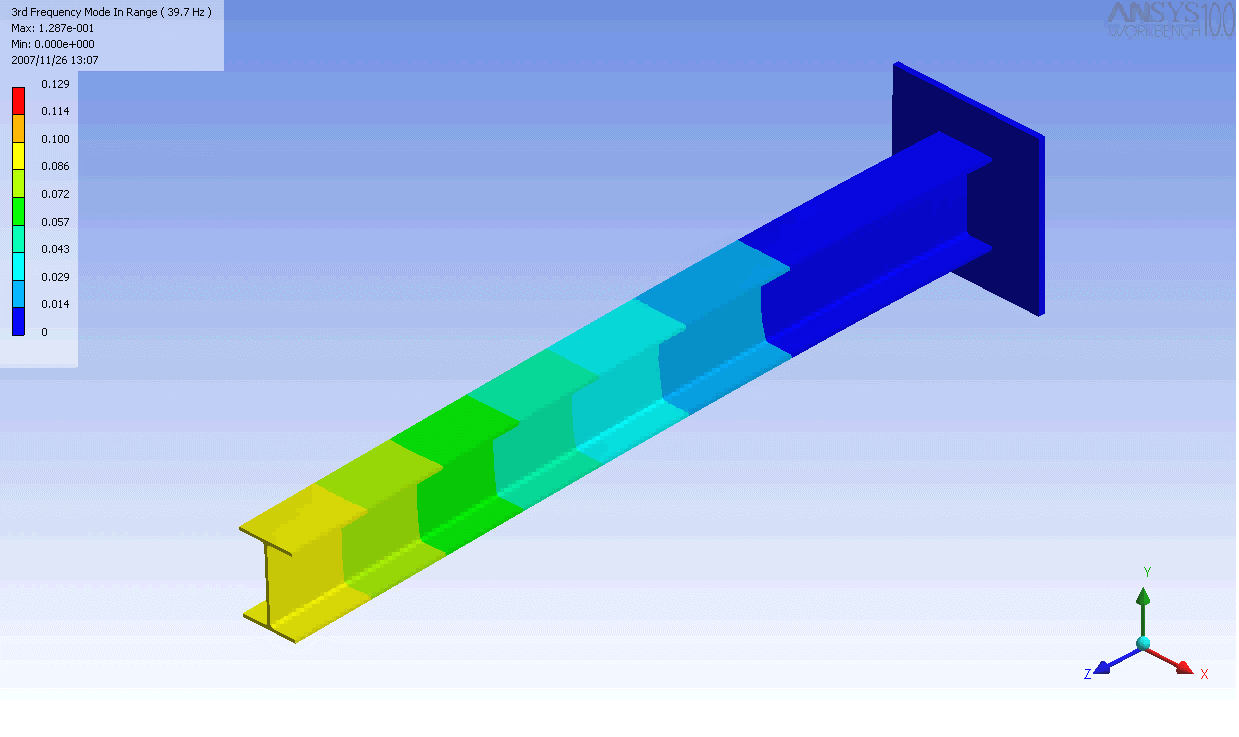
| The mode shapes of a cantilevered -beam | ||
|---|---|---|
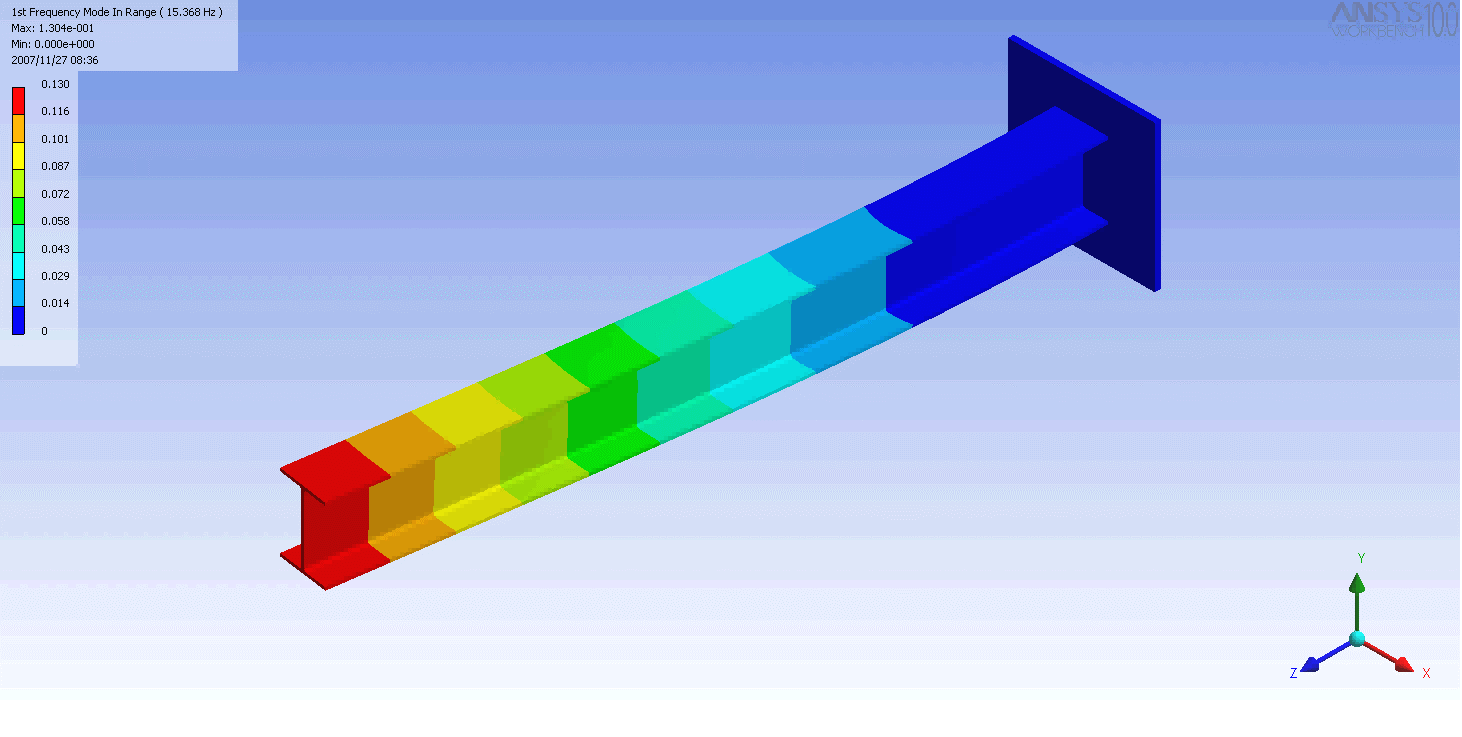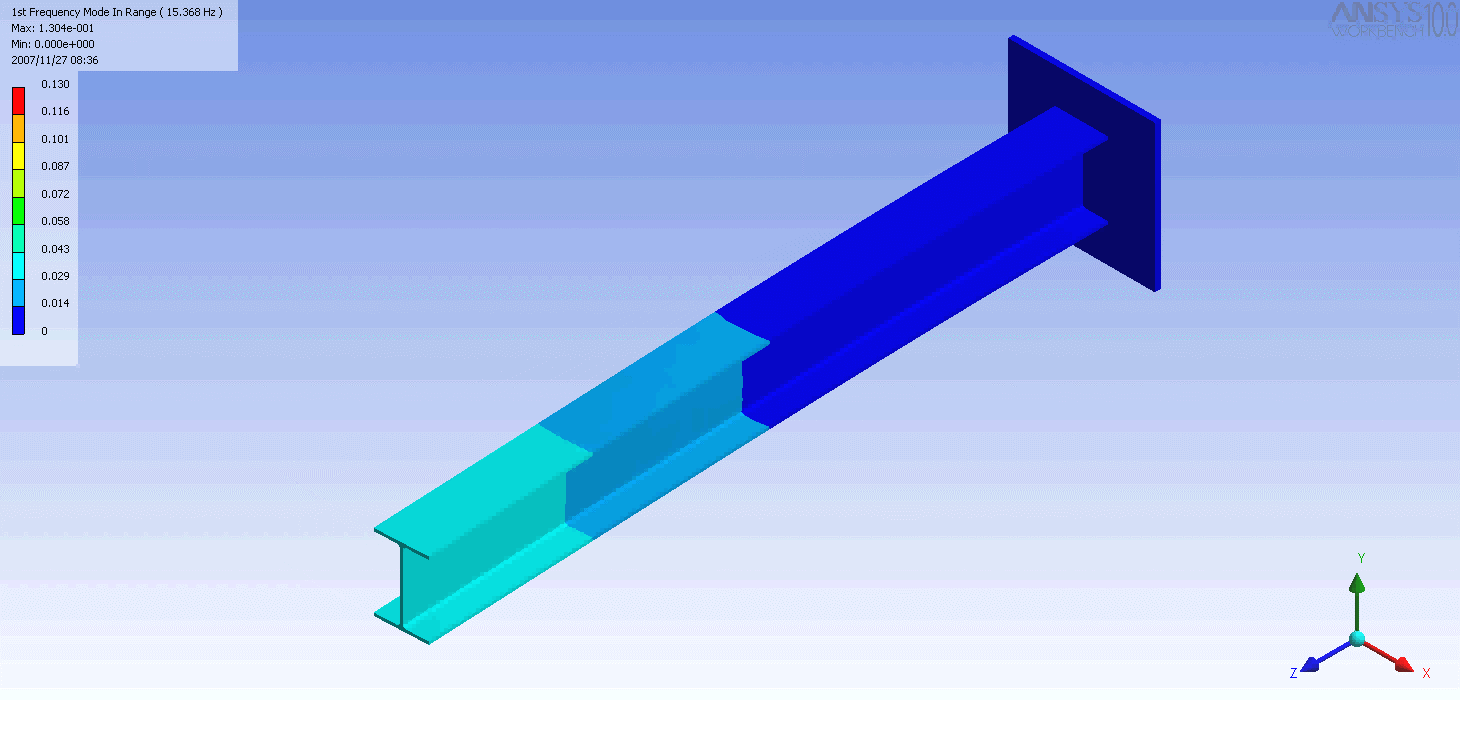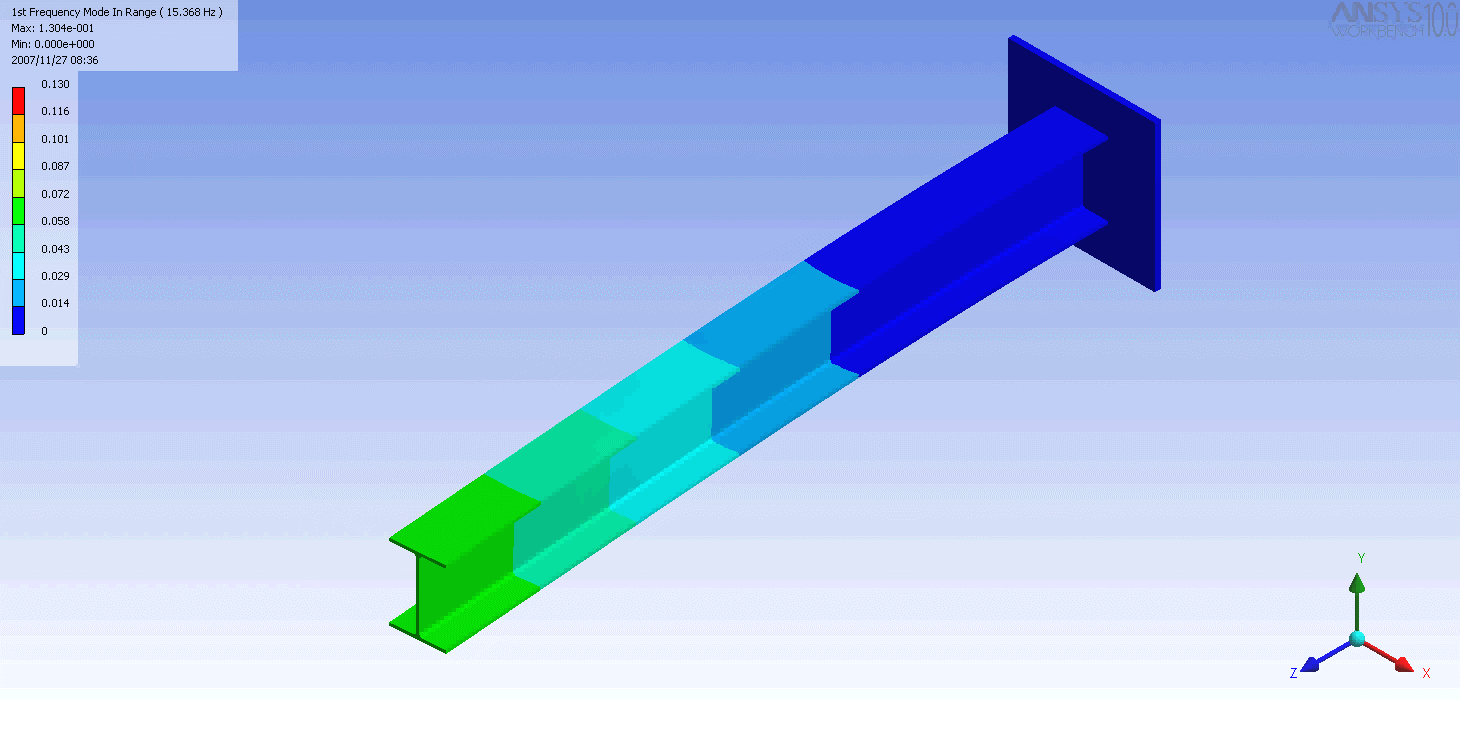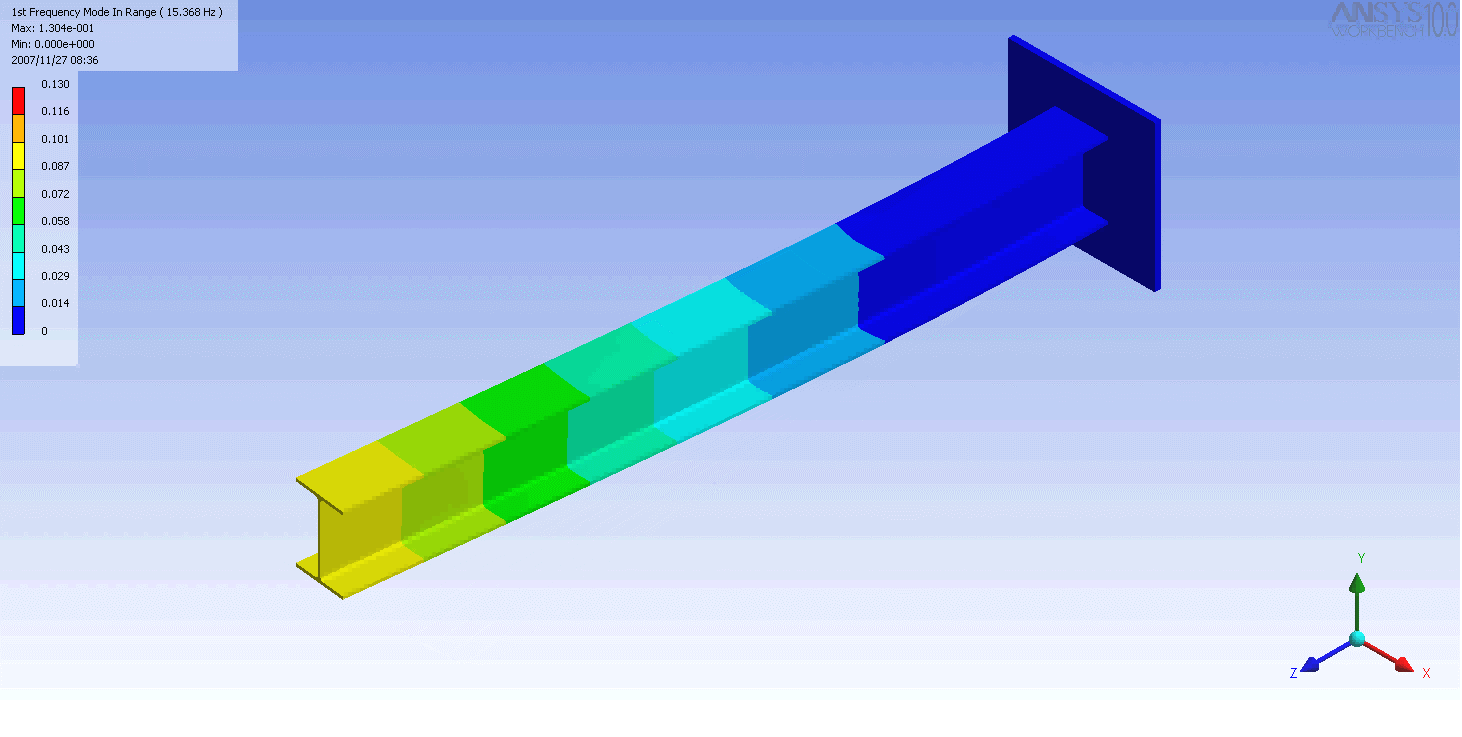 |
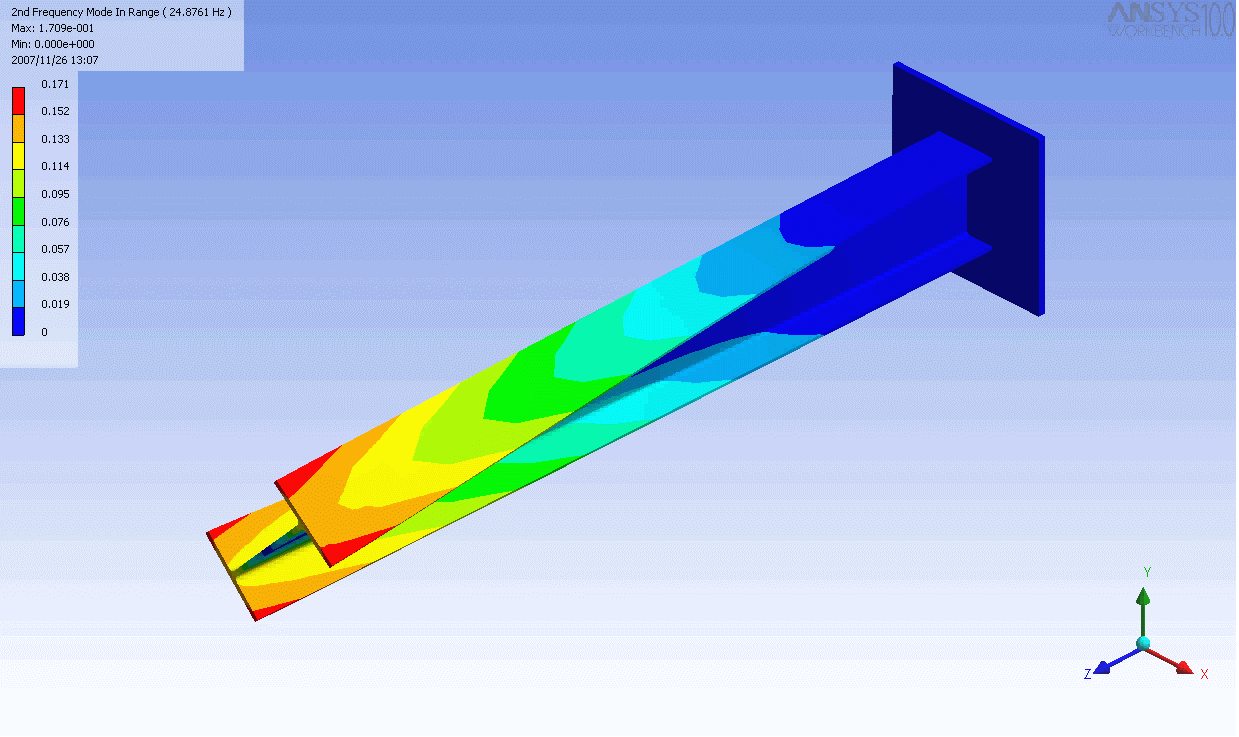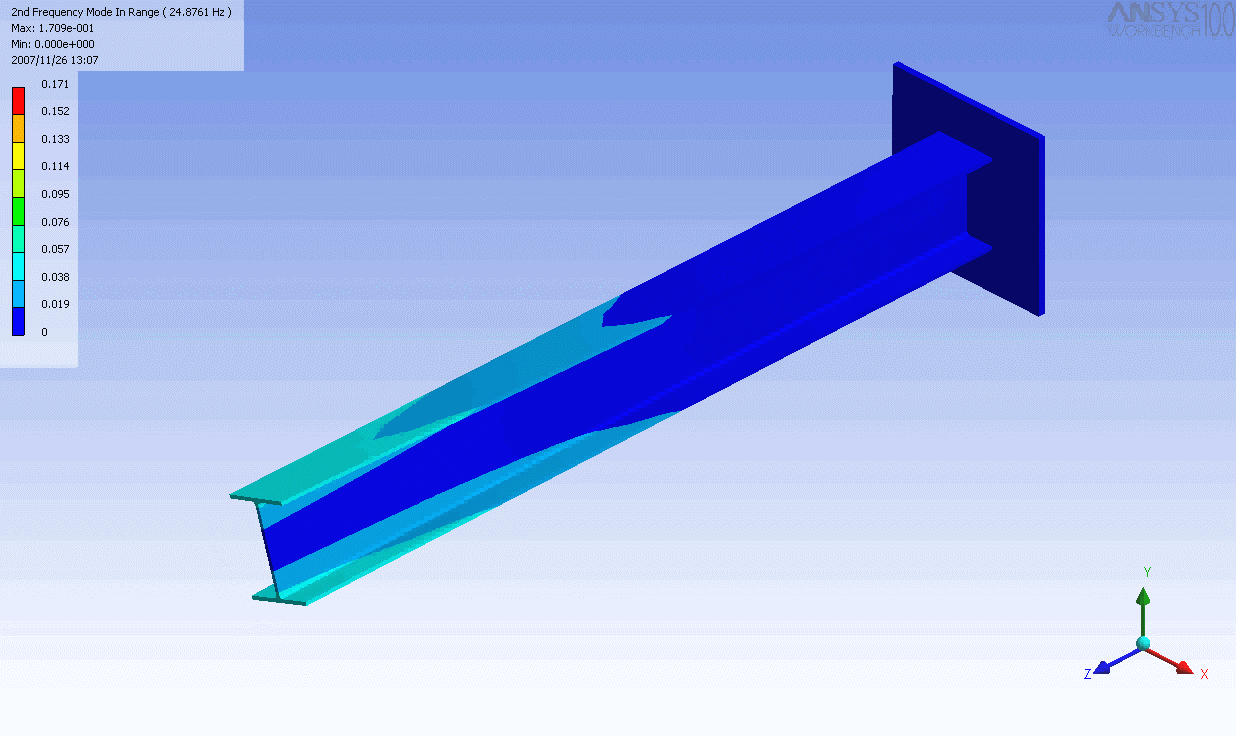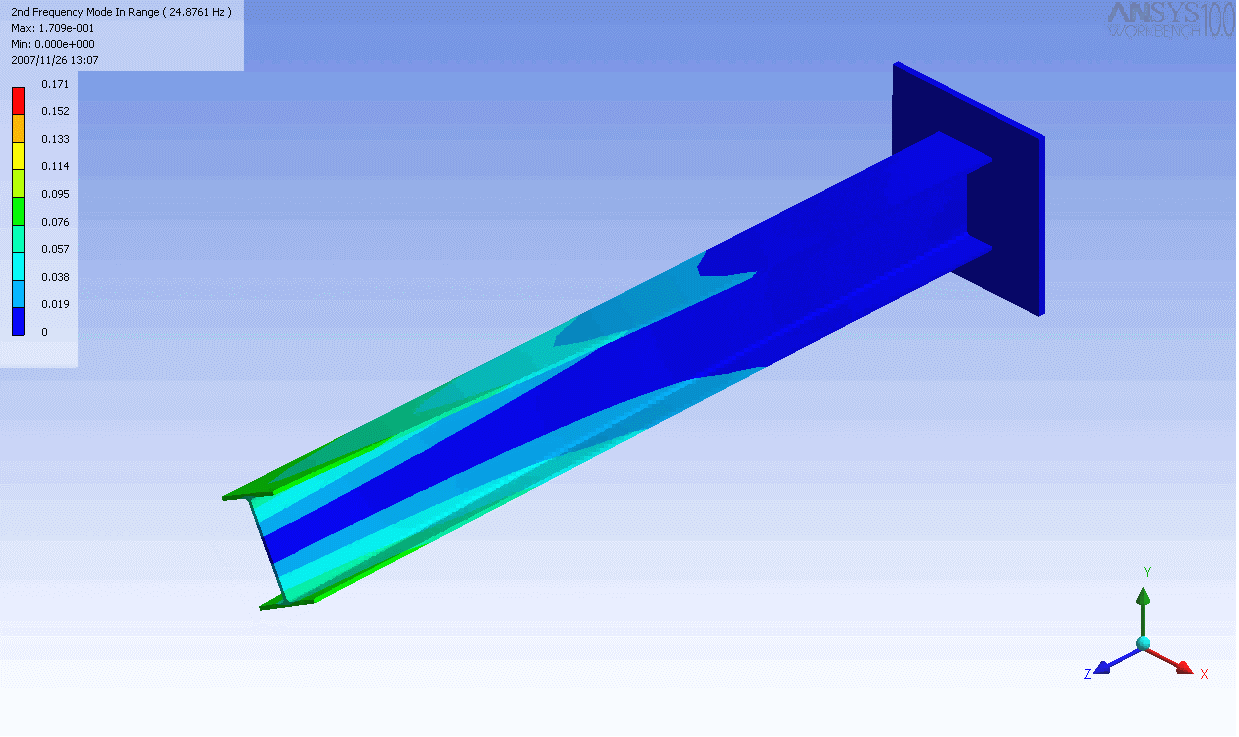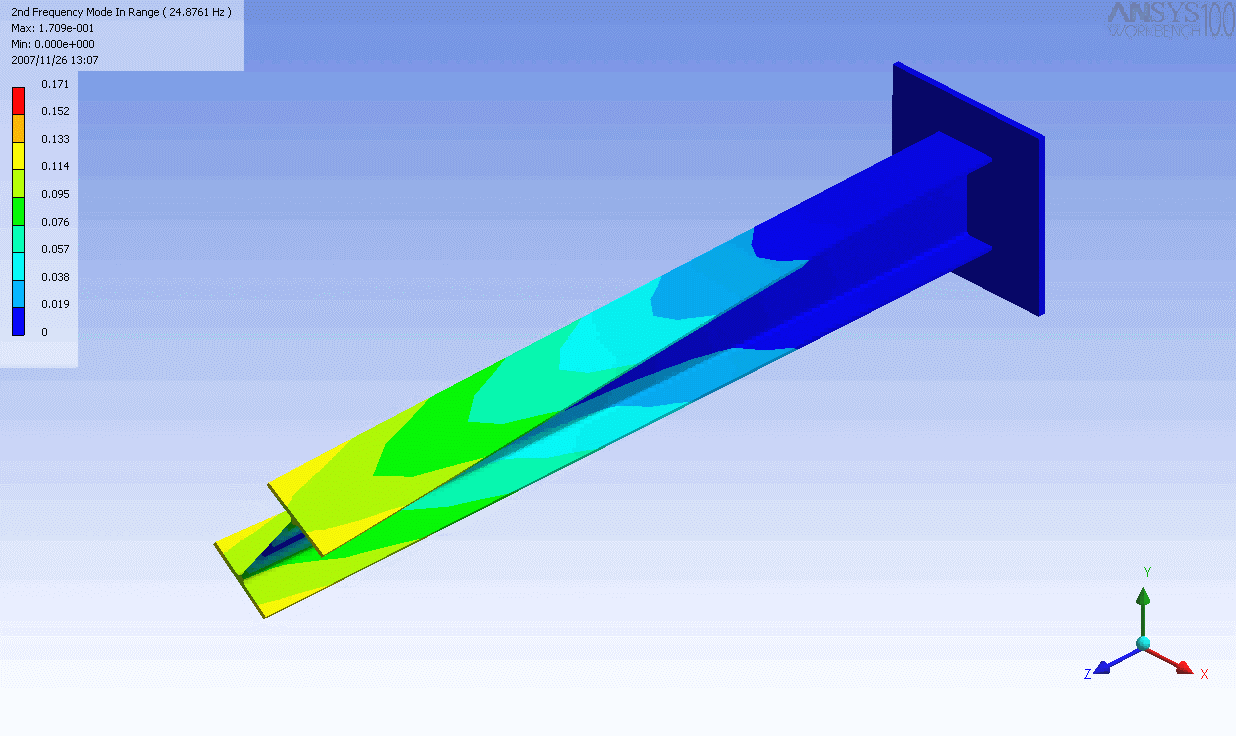 |
 |
 |
 |
 |
Timoshenko-Rayleigh theory
In 1877, Rayleigh proposed an improvement to the dynamic Euler-Bernoulli beam theory by including the effect of rotational inertia of the cross-section of the beam. Timoshenko improved upon that theory in 1922 by adding the effect of shear into the beam equation. Shear deformations of the normal to the mid-surface of the beam are allowed in the Timoshenko-Rayleigh theory.The equation for the bending of a linear elastic, isotropic, homogeneous beam of constant cross-section beam under these assumptions is

where
 is the polar moment of inertia
is the polar moment of inertiaPolar moment of inertia
Polar moment of inertia is a quantity used to predict an object's ability to resist torsion, in objects with an invariant circular cross section and no significant warping or out-of-plane deformation. It is used to calculate the angular displacement of an object subjected to a torque...
of the cross-section,
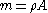 is the mass per unit length of the beam,
is the mass per unit length of the beam, 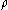 is the density of the beam,
is the density of the beam,  is the cross-sectional area,
is the cross-sectional area, 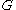 is the shear modulus, and
is the shear modulus, and 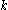 is a shear correction factor. For materials with Poisson's ratios (
is a shear correction factor. For materials with Poisson's ratios ( ) close to 0.3, the shear correction factor are approximately
) close to 0.3, the shear correction factor are approximately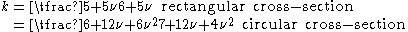
Free vibrations
For free, harmonic vibrations the Timoshenko-Rayleigh equations take the form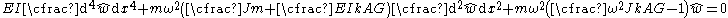
This equation can be solved by noting that all the derivatives of
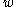 must have the same form to cancel out and hence as solution of the form
must have the same form to cancel out and hence as solution of the form 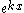 may be expected. This observation leads to the characteristic equation
may be expected. This observation leads to the characteristic equationCharacteristic equation
Characteristic equation may refer to:* Characteristic equation , used to solve linear differential equations* Characteristic equation, a characteristic polynomial equation in linear algebra used to find eigenvalues...
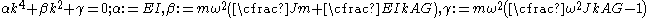
The solutions of this quartic equation are
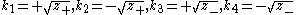
where
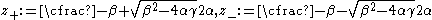
The general solution of the Timoshenko-Rayleigh beam equation for free vibrations can then be written as
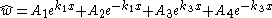
Quasistatic bending of plates
The defining feature of beams is that one of the dimensions is much larger than the other two. A structure is called a plate when it is flat and one of its dimensions is much smaller than the other two. There are several theories that attempt to describe the deformation and stress in a plate under applied loads two of which have been used widely. These are- the Kirchhoff-Love theory of plates (also called classical plate theory)
- the Mindlin-Reissner plate theory (also called the first-order shear theory of plates)
Kirchhoff-Love theory of plates
The assumptions of Kirchhoff-Love theory are- straight lines normal to the mid-surface remain straight after deformation
- straight lines normal to the mid-surface remain normal to the mid-surface after deformation
- the thickness of the plate does not change during a deformation.
These assumptions imply that

where
 is the displacement of a point in the plate and
is the displacement of a point in the plate and 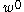 is the displacement of the mid-surface.
is the displacement of the mid-surface.The strain-displacement relations are

The equilibrium equations are
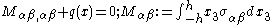
where
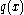 is an applied load normal to the surface of the plate.
is an applied load normal to the surface of the plate.In terms of displacements, the equilibrium equations for an isotropic, linear elastic plate in the absence of external load can be written as
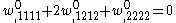
In direct tensor notation,
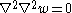
Mindlin-Reissner theory of plates
The special assumption of this theory is that normals to the mid-surface remain straight and inextensible but not necessarily normal to the mid-surface after deformation. The displacements of the plate are given by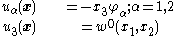
where
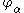 are the rotations of the normal.
are the rotations of the normal.The strain-displacement relations that result from these assumptions are
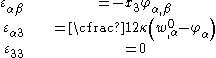
where
 is a shear correction factor.
is a shear correction factor.The equilibrium equations are
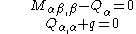
where

Dynamics of thin Kirchhoff plates
The dynamic theory of plates determines the propagation of waves in the plates, and the study of standing waves and vibration modes. The equations that govern the dynamic bending of Kirchhoff plates are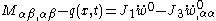
where, for a plate with density
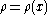 ,
,
and

The figures below show some vibrational modes of a circular plate.
See also
- Bending of platesBending of platesBending of plates or plate bending refers to the deflection of a plate perpendicular to the plane of the plate under the action of external forces and moments. The amount of deflection can be determined by solving the differential equations of an appropriate plate theory. The stresses in the...
- ContraflexureContraflexureIn a bending beam, a point is known as a point of contraflexure if it is a location at which no bending occurs. In a bending moment diagram, it is the point at which the bending moment curve intersects with the zero line...
- Flexure bearingFlexure bearingA flexure bearing is a bearing which allows motion by bending a load element.A typical flexure bearing is just one part, joining two other parts. For example, a hinge may be made by attaching a long strip of a flexible element to a door and to the door frame...
- Shear strengthShear strengthShear strength in engineering is a term used to describe the strength of a material or component against the type of yield or structural failure where the material or component fails in shear. A shear load is a force that tends to produce a sliding failure on a material along a plane that is...
- Sandwich theorySandwich theorySandwich theory describes the behaviour of a beam, plate, or shell which consists of three layers - two facesheets and one core. The most commonly used sandwich theory is linear and is an extension of first order beam theory...
- Timoshenko beam theoryTimoshenko beam theoryThe Timoshenko beam theory was developed by Ukrainian-born scientist Stephen Timoshenko in the beginning of the 20th century. The model takes into account shear deformation and rotational inertia effects, making it suitable for describing the behaviour of short beams, sandwich composite beams or...
- VibrationVibrationVibration refers to mechanical oscillations about an equilibrium point. The oscillations may be periodic such as the motion of a pendulum or random such as the movement of a tire on a gravel road.Vibration is occasionally "desirable"...
- Vibration of platesVibration of platesThe vibration of plates is a special case of the more general problem of mechanical vibrations. The equations governing the motion of plates are simpler than those for general three-dimensional objects because one of the dimensions of a plate is much smaller than the other two...
- List of area moments of inertia