
Ferdinand Georg Frobenius
Encyclopedia
Ferdinand Georg Frobenius (October 26, 1849 – August 3, 1917) was a German
mathematician
, best known for his contributions to the theory of differential equations and to group theory
. He also gave the first full proof for the Cayley–Hamilton theorem.
, a suburb of Berlin
from parents Christian Ferdinand Frobenius, a Protestant parson, and Christine Elizabeth Friedrich. He entered the Joachimsthal Gymnasium in 1860 when he was nearly eleven. In 1867, after graduating, he went to the University of Göttingen where he began his university studies but he only studied there for one semester before returning to Berlin, where he attended lectures by Kronecker, Kummer and Karl Weierstrass
. He received his doctorate (awarded with distinction) in 1870 supervised by Weierstrass. His thesis, supervised by Weierstrass
, was on the solution of differential equations. In 1874, after having taught at secondary school level first at the Joachimsthal Gymnasium then at the Sophienrealschule, he was appointed to the University of Berlin as an extraordinary professor of mathematics. Frobenius was only in Berlin a year before he went to Zürich
to take up an appointment as an ordinary professor at the Eidgenössische Polytechnikum
. For seventeen years, between 1875 and 1892, Frobenius worked in Zürich. He married there, brought up his family and did much important work in widely differing areas of mathematics. In the last days of December 1891 Kronecker died and, therefore, his chair in Berlin became vacant. Weierstrass, strongly believing that Frobenius was the right person to keep Berlin in the forefront of mathematics, used his considerable influence to have Frobenius appointed. In 1893 he returned to Berlin, where he was elected to the Prussian Academy of Sciences
.
was one of Frobenius' principal interests in the second half of his career. One of his first contributions was the proof of the Sylow theorems for abstract groups. Earlier proofs had been for permutation group
s. His proof of the first Sylow theorem (on the existence of Sylow groups) is one of those frequently used today.
More important was his creation of the theory of group characters and group representation
s, which are fundamental tools for studying the structure of groups. This work led to the notion of Frobenius reciprocity
and the definition of what are now called Frobenius group
s. A group G is said to be a Frobenius group if there is a subgroup H < G such that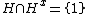 for all
for all 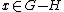 .
.
In that case, the set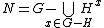
together with the identity element of G forms a subgroup which is nilpotent
as Thompson showed in his PhD thesis. All known proofs of that theorem make use of characters. In his first paper about characters (1896), Frobenius constructed the character table of the group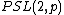 of order (1/2)(p3 − p) for all odd primes p (this group is simple provided p > 3). He also
of order (1/2)(p3 − p) for all odd primes p (this group is simple provided p > 3). He also
made fundamental contributions to the representation theory of the symmetric and alternating groups.
s over Q. Specifically, if K/Q is a finite Galois extension then to each (positive) prime p which does not ramify
in K and to each prime ideal P lying over p in K there is a unique element g of Gal(K/Q) satisfying the condition g(x) = xp (mod P) for all integers x of K. Varying P over p changes g into a conjugate (and every conjugate of g occurs in this way), so the conjugacy class of g in the Galois group is canonically associated to p. This is called the Frobenius conjugacy class of p and any element of
the conjugacy class is called a Frobenius element of p. If we take for K the mth cyclotomic field
, whose Galois group over Q is the units modulo m (and thus
is abelian, so conjugacy classes become elements), then for p not dividing m the Frobenius class in the Galois group is p mod m. From this point of view,
the distribution of Frobenius conjugacy classes in Galois groups over Q (or, more generally, Galois groups over any number field) generalizes Dirichlet's classical result about primes in arithmetic progressions. The study of Galois groups of infinite-degree extensions of Q depends crucially on this construction of Frobenius elements, which provides in a sense a dense subset of elements which are accessible to detailed study.
Germans
The Germans are a Germanic ethnic group native to Central Europe. The English term Germans has referred to the German-speaking population of the Holy Roman Empire since the Late Middle Ages....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
, best known for his contributions to the theory of differential equations and to group theory
Group theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
. He also gave the first full proof for the Cayley–Hamilton theorem.
Biography
Ferdinand Georg Frobenius was born on October 26, 1849 in CharlottenburgCharlottenburg
Charlottenburg is a locality of Berlin within the borough of Charlottenburg-Wilmersdorf, named after Queen consort Sophia Charlotte...
, a suburb of Berlin
Berlin
Berlin is the capital city of Germany and is one of the 16 states of Germany. With a population of 3.45 million people, Berlin is Germany's largest city. It is the second most populous city proper and the seventh most populous urban area in the European Union...
from parents Christian Ferdinand Frobenius, a Protestant parson, and Christine Elizabeth Friedrich. He entered the Joachimsthal Gymnasium in 1860 when he was nearly eleven. In 1867, after graduating, he went to the University of Göttingen where he began his university studies but he only studied there for one semester before returning to Berlin, where he attended lectures by Kronecker, Kummer and Karl Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
. He received his doctorate (awarded with distinction) in 1870 supervised by Weierstrass. His thesis, supervised by Weierstrass
Karl Weierstrass
Karl Theodor Wilhelm Weierstrass was a German mathematician who is often cited as the "father of modern analysis".- Biography :Weierstrass was born in Ostenfelde, part of Ennigerloh, Province of Westphalia....
, was on the solution of differential equations. In 1874, after having taught at secondary school level first at the Joachimsthal Gymnasium then at the Sophienrealschule, he was appointed to the University of Berlin as an extraordinary professor of mathematics. Frobenius was only in Berlin a year before he went to Zürich
Zürich
Zurich is the largest city in Switzerland and the capital of the canton of Zurich. It is located in central Switzerland at the northwestern tip of Lake Zurich...
to take up an appointment as an ordinary professor at the Eidgenössische Polytechnikum
ETH Zurich
The Swiss Federal Institute of Technology Zurich or ETH Zürich is an engineering, science, technology, mathematics and management university in the City of Zurich, Switzerland....
. For seventeen years, between 1875 and 1892, Frobenius worked in Zürich. He married there, brought up his family and did much important work in widely differing areas of mathematics. In the last days of December 1891 Kronecker died and, therefore, his chair in Berlin became vacant. Weierstrass, strongly believing that Frobenius was the right person to keep Berlin in the forefront of mathematics, used his considerable influence to have Frobenius appointed. In 1893 he returned to Berlin, where he was elected to the Prussian Academy of Sciences
Prussian Academy of Sciences
The Prussian Academy of Sciences was an academy established in Berlin on 11 July 1700, four years after the Akademie der Künste or "Arts Academy", to which "Berlin Academy" may also refer.-Origins:...
.
Contributions to group theory
Group theoryGroup theory
In mathematics and abstract algebra, group theory studies the algebraic structures known as groups.The concept of a group is central to abstract algebra: other well-known algebraic structures, such as rings, fields, and vector spaces can all be seen as groups endowed with additional operations and...
was one of Frobenius' principal interests in the second half of his career. One of his first contributions was the proof of the Sylow theorems for abstract groups. Earlier proofs had been for permutation group
Permutation group
In mathematics, a permutation group is a group G whose elements are permutations of a given set M, and whose group operation is the composition of permutations in G ; the relationship is often written as...
s. His proof of the first Sylow theorem (on the existence of Sylow groups) is one of those frequently used today.
- Frobenius also has proved the following fundamental theorem: If a positive integer n divides the order |G| of a finite groupFinite groupIn mathematics and abstract algebra, a finite group is a group whose underlying set G has finitely many elements. During the twentieth century, mathematicians investigated certain aspects of the theory of finite groups in great depth, especially the local theory of finite groups, and the theory of...
G, then the number of solutions of the equation xn = 1 in G is equal to kn for some positive integer k. He also posed the following problem: If, in the above theorem, k = 1, then the solutions of the equation xn = 1 in G form a subgroup. Many years ago this problem was solved for solvable groupSolvable groupIn mathematics, more specifically in the field of group theory, a solvable group is a group that can be constructed from abelian groups using extensions...
s (see textbook by Marshall Hall Jr., Theorem 9.4.1). Only in 1991, after the classification of finite simple groupsClassification of finite simple groupsIn mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
, was this problem solved in general.
More important was his creation of the theory of group characters and group representation
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
s, which are fundamental tools for studying the structure of groups. This work led to the notion of Frobenius reciprocity
Character theory
In mathematics, more specifically in group theory, the character of a group representation is a function on the group which associates to each group element the trace of the corresponding matrix....
and the definition of what are now called Frobenius group
Frobenius group
In mathematics, a Frobenius group is a transitive permutation group on a finite set, such that no non-trivial elementfixes more than one point and some non-trivial element fixes a point.They are named after F. G. Frobenius.- Structure :...
s. A group G is said to be a Frobenius group if there is a subgroup H < G such that
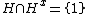 for all
for all 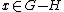 .
.In that case, the set
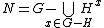
together with the identity element of G forms a subgroup which is nilpotent
Nilpotent group
In mathematics, more specifically in the field of group theory, a nilpotent group is a group that is "almost abelian". This idea is motivated by the fact that nilpotent groups are solvable, and for finite nilpotent groups, two elements having relatively prime orders must commute...
as Thompson showed in his PhD thesis. All known proofs of that theorem make use of characters. In his first paper about characters (1896), Frobenius constructed the character table of the group
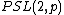 of order (1/2)(p3 − p) for all odd primes p (this group is simple provided p > 3). He also
of order (1/2)(p3 − p) for all odd primes p (this group is simple provided p > 3). He alsomade fundamental contributions to the representation theory of the symmetric and alternating groups.
Contributions to number theory
Frobenius introduced a canonical way of turning primes into conjugacy classes in Galois groupGalois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
s over Q. Specifically, if K/Q is a finite Galois extension then to each (positive) prime p which does not ramify
Ramification
In mathematics, ramification is a geometric term used for 'branching out', in the way that the square root function, for complex numbers, can be seen to have two branches differing in sign...
in K and to each prime ideal P lying over p in K there is a unique element g of Gal(K/Q) satisfying the condition g(x) = xp (mod P) for all integers x of K. Varying P over p changes g into a conjugate (and every conjugate of g occurs in this way), so the conjugacy class of g in the Galois group is canonically associated to p. This is called the Frobenius conjugacy class of p and any element of
the conjugacy class is called a Frobenius element of p. If we take for K the mth cyclotomic field
Cyclotomic field
In number theory, a cyclotomic field is a number field obtained by adjoining a complex primitive root of unity to Q, the field of rational numbers...
, whose Galois group over Q is the units modulo m (and thus
is abelian, so conjugacy classes become elements), then for p not dividing m the Frobenius class in the Galois group is p mod m. From this point of view,
the distribution of Frobenius conjugacy classes in Galois groups over Q (or, more generally, Galois groups over any number field) generalizes Dirichlet's classical result about primes in arithmetic progressions. The study of Galois groups of infinite-degree extensions of Q depends crucially on this construction of Frobenius elements, which provides in a sense a dense subset of elements which are accessible to detailed study.

