
Transitivity (mathematics)
Encyclopedia
In grammar
- Intransitive verbIntransitive verbIn grammar, an intransitive verb is a verb that has no object. This differs from a transitive verb, which takes one or more objects. Both classes of verb are related to the concept of the transitivity of a verb....
- Transitive verbTransitive verbIn syntax, a transitive verb is a verb that requires both a direct subject and one or more objects. The term is used to contrast intransitive verbs, which do not have objects.-Examples:Some examples of sentences with transitive verbs:...
, when a verb takes an object - Transitivity (grammar)
In logic and mathematics
- Arc-transitive graph
- Edge-transitive graphEdge-transitive graphIn the mathematical field of graph theory, an edge-transitive graph is a graph G such that, given any two edges e1 and e2 of G, there is anautomorphism of G that maps e1 to e2....
- Ergodic theoryErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
, a group action that is metrically transitive - Vertex-transitive graphVertex-transitive graphIn the mathematical field of graph theory, a vertex-transitive graph is a graph G such that, given any two vertices v1 and v2 of G, there is some automorphismf:V \rightarrow V\ such thatf = v_2.\...
- A groupGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G acts transitively on a set S if for any x, y ∈ S, there is some g ∈ G such that gx = y. See group actionGroup actionIn algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
. A somewhat related meaning is explained at ergodic theoryErgodic theoryErgodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
. - A binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
is transitive if whenever A is related to B and B is related to C, then A is related to C, for all A, B, and C in the domain of the relation. See transitive relationTransitive relationIn mathematics, a binary relation R over a set X is transitive if whenever an element a is related to an element b, and b is in turn related to an element c, then a is also related to c....
. - A transitive setTransitive setIn set theory, a set A is transitive, if* whenever x ∈ A, and y ∈ x, then y ∈ A, or, equivalently,* whenever x ∈ A, and x is not an urelement, then x is a subset of A....
is a set A such that whenever x ∈ A, and y ∈ x, then y ∈ A. The smallest transitive set containing a set A is called the transitive closureTransitive closureIn mathematics, the transitive closure of a binary relation R on a set X is the transitive relation R+ on set X such that R+ contains R and R+ is minimal . If the binary relation itself is transitive, then the transitive closure will be that same binary relation; otherwise, the transitive closure...
of A. - A discrete dynamical system f is topologically transitive if every open subset U of the phase space intersects every other open subset V, when going along trajectory, i.e. there exists an integer n, for which
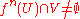 .
.

