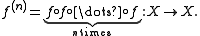In measure theory, a pushforward measure (also push forward, push-forward or image measure ) is obtained by transferring ("pushing forward") a measure

Measure (mathematics)

In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

 from one measurable space to another using a measurable function

Measurable function

In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

.

Definition

Given measurable spaces (X₁, Σ₁) and (X₂, Σ₂), a measurable function f : X₁ → X₂ and a measure μ : Σ₁ → [0, +∞], the pushforward of μ is defined to be the measure f_∗(μ) : Σ₂ → [0, +∞] given by


This definition applies mutatis mutandis

Mutatis mutandis

Mutatis mutandis is a Latin phrase meaning "by changing those things which need to be changed" or more simply "the necessary changes having been made"....

for a signed

Signed measure

In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...

 or complex measure

Complex measure

In mathematics, specifically measure theory, a complex measure generalizes the concept of measure by letting it have complex values. In other words, one allows for sets whose size is a complex number.-Definition:...

.

Examples and applications

• A natural "Lebesgue measure
  Lebesgue measure
  In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
  
  " on the unit circle
  Unit circle
  In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
  
   S¹ (here thought of as a subset of the complex plane
  Complex plane
  In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
  
   C) may be defined using a push-forward construction and Lebesgue measure λ on the real line
  Real line
  In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
  
   R. Let λ also denote the restriction of Lebesgue measure to the interval [0, 2π) and let f : [0, 2π) → S¹ be the natural bijection defined by f(t) = exp(i t). The natural "Lebesgue measure" on S¹ is then the push-forward measure f_∗(λ). The measure f_∗(λ) might also be called "arc length
  Arc length
  Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
  
   measure" or "angle measure", since the f_∗(λ)-measure of an arc in S¹ is precisely its arc length (or, equivalently, the angle that it subtends at the centre of the circle.)

• The previous example extends nicely to give a natural "Lebesgue measure" on the n-dimensional torus
  Torus
  In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
  
   Tⁿ. The previous example is a special case, since S¹ = T¹. This Lebesgue measure on Tⁿ is, up to normalization, the Haar measure
  Haar measure
  In mathematical analysis, the Haar measure is a way to assign an "invariant volume" to subsets of locally compact topological groups and subsequently define an integral for functions on those groups....
  
   for the compact
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
  , connected
  Connected space
  In topology and related branches of mathematics, a connected space is a topological space that cannot be represented as the union of two or more disjoint nonempty open subsets. Connectedness is one of the principal topological properties that is used to distinguish topological spaces...
  
   Lie group
  Lie group
  In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
  
   Tⁿ.

• Gaussian measure
  Gaussian measure
  In mathematics, Gaussian measure is a Borel measure on finite-dimensional Euclidean space Rn, closely related to the normal distribution in statistics. There is also a generalization to infinite-dimensional spaces...
  
  s on infinite-dimensional vector spaces are defined using the push-forward and the standard Gaussian measure on the real line: a Borel measure γ on a separable Banach space
  Banach space
  In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
  
   X is called Gaussian if the push-forward of γ by any non-zero linear functional
  Linear functional
  In linear algebra, a linear functional or linear form is a linear map from a vector space to its field of scalars.  In Rn, if vectors are represented as column vectors, then linear functionals are represented as row vectors, and their action on vectors is given by the dot product, or the...
  
   in the continuous dual space to X is a Gaussian measure on R.

• Consider a measurable function f : X → X and the composition
  Function composition
  In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
  
   of f with itself n times:

This iterated function

Iterated function

In mathematics, an iterated function is a function which is composed with itself, possibly ad infinitum, in a process called iteration. In this process, starting from some initial value, the result of applying a given function is fed again in the function as input, and this process is repeated...

 forms a dynamical system

Dynamical system

A dynamical system is a concept in mathematics where a fixed rule describes the time dependence of a point in a geometrical space. Examples include the mathematical models that describe the swinging of a clock pendulum, the flow of water in a pipe, and the number of fish each springtime in a...

. It is often of interest in the study of such systems to find a measure μ on X that the map f leaves unchanged, a so-called invariant measure

Invariant measure

In mathematics, an invariant measure is a measure that is preserved by some function. Ergodic theory is the study of invariant measures in dynamical systems...

, one for which f_∗(μ) = μ.

• One can also consider quasi-invariant measure
  Quasi-invariant measure
  In mathematics, a quasi-invariant measure μ with respect to a transformation T, from a measure space X to itself, is a measure which, roughly speaking, is multiplied by a numerical function by T...
  
  s for such a dynamical system: a measure μ on X is called quasi-invariant under f if the push-forward of μ by f is merely equivalent to the original measure μ, not necessarily equal to it.

A generalization

In general, any measurable function

Measurable function

In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...

 can be pushed forward, the push-forward then becomes a linear operator, known as the transfer operator

Transfer operator

In mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...

 or Frobenius–Perron operator. This operator typically satisfies the requirements of the Frobenius–Perron theorem, and the maximal eigenvalue of this theorem corresponds to the invariant measure. The adjoint to the push-forward is the pullback

Pullback

Suppose that φ:M→ N is a smooth map between smooth manifolds M and N; then there is an associated linear map from the space of 1-forms on N to the space of 1-forms on M. This linear map is known as the pullback , and is frequently denoted by φ*...

; as an operator on measurable spaces, it is the composition operator

Composition operator

In mathematics, the composition operator C_\phi with symbol \phi is a linear operator defined by the ruleC_\phi = f \circ\phiwhere f \circ\phi denotes function composition. In physics, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman...

 or Koopman operator.