
Composition operator
Encyclopedia
In mathematics
, the composition operator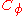 with symbol
with symbol  is a linear operator defined by the rule
is a linear operator defined by the rule
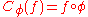
where denotes function composition
denotes function composition
. In physics
, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman operator. It is the left-adjoint of the Frobenius-Perron or transfer operator
. In the language of category theory
, the composition operator is a pull-back on the space of measurable function
s; it is adjoint to the transfer operator in the same way that the pull-back is adjoint to the push-forward; the composition operator is the inverse image functor
.
The domain of a composition operator is usually taken to be some Banach space
, often consisting of holomorphic function
s: for example, some Hardy space
or Bergman space
. Interesting questions posed in the study of composition operators often relate to how the spectral properties
of the operator depend on the function space. Other questions include whether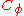 is compact
is compact
or trace-class; answers typically depend on how the function behaves on the boundary of some domain.
behaves on the boundary of some domain.
In mathematics, composition operators commonly occur in the study of shift operator
s, for example, in the Beurling-Lax theorem and the Wold decomposition
. Shift operators can be studied as one-dimensional spin lattices. Composition operators appear in the theory of Aleksandrov-Clark measure
s.
The eigenvalue equation of the composition operator is Schröder's equation.
The study of composition operators is covered by AMS category 47B33.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the composition operator
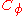 with symbol
with symbol  is a linear operator defined by the rule
is a linear operator defined by the rule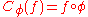
where
 denotes function composition
denotes function compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. In physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, and especially the area of dynamical systems, the composition operator is usually referred to as the Koopman operator. It is the left-adjoint of the Frobenius-Perron or transfer operator
Transfer operator
In mathematics, the transfer operator encodes information about an iterated map and is frequently used to study the behavior of dynamical systems, statistical mechanics, quantum chaos and fractals...
. In the language of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, the composition operator is a pull-back on the space of measurable function
Measurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
s; it is adjoint to the transfer operator in the same way that the pull-back is adjoint to the push-forward; the composition operator is the inverse image functor
Inverse image functor
In mathematics, the inverse image functor is a contravariant construction of sheaves. The direct image functor is the primary operation on sheaves, with the simplest definition. The inverse image exhibits some relatively subtle features.-Definition:...
.
The domain of a composition operator is usually taken to be some Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
, often consisting of holomorphic function
Holomorphic function
In mathematics, holomorphic functions are the central objects of study in complex analysis. A holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighborhood of every point in its domain...
s: for example, some Hardy space
Hardy space
In complex analysis, the Hardy spaces Hp are certain spaces of holomorphic functions on the unit disk or upper half plane. They were introduced by Frigyes Riesz , who named them after G. H. Hardy, because of the paper...
or Bergman space
Bergman space
In complex analysis, a branch of mathematics, a Bergman space, named after Stefan Bergman, is a function space of holomorphic functions in a domain D of the complex plane that are sufficiently well-behaved at the boundary that they are absolutely integrable...
. Interesting questions posed in the study of composition operators often relate to how the spectral properties
Spectrum (functional analysis)
In functional analysis, the concept of the spectrum of a bounded operator is a generalisation of the concept of eigenvalues for matrices. Specifically, a complex number λ is said to be in the spectrum of a bounded linear operator T if λI − T is not invertible, where I is the...
of the operator depend on the function space. Other questions include whether
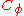 is compact
is compactCompact operator
In functional analysis, a branch of mathematics, a compact operator is a linear operator L from a Banach space X to another Banach space Y, such that the image under L of any bounded subset of X is a relatively compact subset of Y...
or trace-class; answers typically depend on how the function
 behaves on the boundary of some domain.
behaves on the boundary of some domain.In mathematics, composition operators commonly occur in the study of shift operator
Shift operator
In mathematics, and in particular functional analysis, the shift operator or translation operator is an operator that takes a function to its translation . In time series analysis, the shift operator is called the lag operator....
s, for example, in the Beurling-Lax theorem and the Wold decomposition
Wold decomposition
In operator theory, the Wold decomposition, named after Herman Wold, or Wold-von Neumann decomposition, after Wold and John von Neumann, is a classification theorem for isometric linear operators on a given Hilbert space...
. Shift operators can be studied as one-dimensional spin lattices. Composition operators appear in the theory of Aleksandrov-Clark measure
Aleksandrov-Clark measure
In mathematics, Aleksandrov–Clark measures are specially constructed measures named after the two mathematicians, A. B. Aleksandrov and Douglas Clark, who discovered some of their deepest properties...
s.
The eigenvalue equation of the composition operator is Schröder's equation.
The study of composition operators is covered by AMS category 47B33.

