
Complex measure
Encyclopedia
In mathematics
, specifically measure theory, a complex measure generalizes the concept of measure
by letting it have complex
values. In other words, one allows for sets whose size (length, area, volume) is a complex number.
(X,Σ) is a function
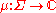
defined on Σ and taking complex values, which is sigma-additive
; that is, for any sequence
(An)n of disjoint sets in Σ one has

provided that the sum on the right converges absolutely or diverges properly, by analogy with the real-valued signed measures.
with respect to a complex measure in the same way as the Lebesgue integral of a real-valued measurable function with respect to a non-negative measure
, by approximating a measurable function with simple function
s. Just as in the case of ordinary integration, this more general integral might fail to exist, or its value might be infinite (the complex infinity
).
Another approach is to not develop a theory of integration from scratch, but rather use the already available concept of integral of a real-valued function with respect to a non-negative measure. To that end, it is a quick check that the real and imaginary parts μ1 and μ2 of a complex measure μ are finite-valued signed measure
s. One can apply the Hahn-Jordan decomposition
to these measures to split them as
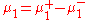
and
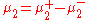
where μ1+, μ1-, μ2+, μ2- are finite-valued non-negative measures (unique in some sense). Then, for a measurable function f which is real-valued for the moment, one can define
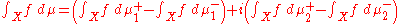
as long as the expression on the right-hand side is defined, that is, all four integrals exist and when adding them up one does not encounter the indeterminate
∞−∞.
Given now a complex-valued measurable function, one can integrate its real and imaginary components separately as illustrated above and define, as expected,
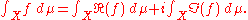

where A is in Σ and the supremum
runs over all sequences of disjoint sets (An)n whose union is A. Taking only finite partitions of the set A into measurable subsets, one obtains an equivalent definition.
It turns out that |μ| is a non-negative finite measure. In the same way as a complex number can be represented in a polar form
, one has a polar decomposition for a complex measure: There exists a measurable function θ with real values such that

meaning
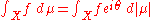
for any absolutely integrable measurable function f, i.e., f satisfying

One can use the Radon–Nikodym theorem
to prove that the variation is a measure and the existence of the polar decomposition.
. Moreover, the total variation
||μ|| defined as

is a norm
in respect to which the space of complex measures is a Banach space
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically measure theory, a complex measure generalizes the concept of measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
by letting it have complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
values. In other words, one allows for sets whose size (length, area, volume) is a complex number.
Definition
Formally, a complex measure μ on a measurable spaceSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
(X,Σ) is a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
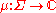
defined on Σ and taking complex values, which is sigma-additive
Sigma additivity
In mathematics, additivity and sigma additivity of a function defined on subsets of a given set are abstractions of the intuitive properties of size of a set.- Additive set functions :...
; that is, for any sequence
Sequence
In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...
(An)n of disjoint sets in Σ one has

provided that the sum on the right converges absolutely or diverges properly, by analogy with the real-valued signed measures.
Integration in respect to a complex measure
One can define the integral of a complex-valued measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
with respect to a complex measure in the same way as the Lebesgue integral of a real-valued measurable function with respect to a non-negative measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
, by approximating a measurable function with simple function
Simple function
In the mathematical field of real analysis, a simple function is a real-valued function over a subset of the real line which attains only a finite number of values...
s. Just as in the case of ordinary integration, this more general integral might fail to exist, or its value might be infinite (the complex infinity
Riemann sphere
In mathematics, the Riemann sphere , named after the 19th century mathematician Bernhard Riemann, is the sphere obtained from the complex plane by adding a point at infinity...
).
Another approach is to not develop a theory of integration from scratch, but rather use the already available concept of integral of a real-valued function with respect to a non-negative measure. To that end, it is a quick check that the real and imaginary parts μ1 and μ2 of a complex measure μ are finite-valued signed measure
Signed measure
In mathematics, signed measure is a generalization of the concept of measure by allowing it to have negative values. Some authors may call it a charge, by analogy with electric charge, which is a familiar distribution that takes on positive and negative values.-Definition:There are two slightly...
s. One can apply the Hahn-Jordan decomposition
Hahn decomposition theorem
In mathematics, the Hahn decomposition theorem, named after the Austrian mathematician Hans Hahn, states that given a measurable space and a signed measure μ defined on the σ-algebra Σ, there exist two sets P and N in Σ such that:...
to these measures to split them as
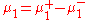
and
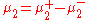
where μ1+, μ1-, μ2+, μ2- are finite-valued non-negative measures (unique in some sense). Then, for a measurable function f which is real-valued for the moment, one can define
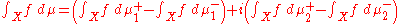
as long as the expression on the right-hand side is defined, that is, all four integrals exist and when adding them up one does not encounter the indeterminate
Indeterminate
Indeterminate has a variety of meanings in mathematics:* Indeterminate * Indeterminate system* Indeterminate equation* Statically indeterminate* Indeterminate formIt is also a term in botany and gardening:*Indeterminate growth...
∞−∞.
Given now a complex-valued measurable function, one can integrate its real and imaginary components separately as illustrated above and define, as expected,
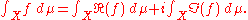
Variation of a complex measure and polar decomposition
For a complex measure μ, one defines its variation, or absolute value, |μ| by the formula
where A is in Σ and the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
runs over all sequences of disjoint sets (An)n whose union is A. Taking only finite partitions of the set A into measurable subsets, one obtains an equivalent definition.
It turns out that |μ| is a non-negative finite measure. In the same way as a complex number can be represented in a polar form
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
, one has a polar decomposition for a complex measure: There exists a measurable function θ with real values such that

meaning
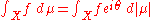
for any absolutely integrable measurable function f, i.e., f satisfying

One can use the Radon–Nikodym theorem
Radon–Nikodym theorem
In mathematics, the Radon–Nikodym theorem is a result in measure theory that states that, given a measurable space , if a σ-finite measure ν on is absolutely continuous with respect to a σ-finite measure μ on , then there is a measurable function f on X and taking values in [0,∞), such that\nu =...
to prove that the variation is a measure and the existence of the polar decomposition.
The space of complex measures
The sum of two complex measures is a complex measure, as is the product of a complex measure by a complex number. That is to say, the set of all complex measures on a measure space (X, Σ) forms a vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
. Moreover, the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
||μ|| defined as

is a norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
in respect to which the space of complex measures is a Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
.
External links
- Complex measure on MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...

