This article describes the distribution function as used in physics. You may be looking for the related mathematical concepts of cumulative distribution function

Cumulative distribution function

In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...

 or probability density function

Probability density function

In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...

.

In molecular kinetic theory

Kinetic theory

The kinetic theory of gases describes a gas as a large number of small particles , all of which are in constant, random motion. The rapidly moving particles constantly collide with each other and with the walls of the container...

 in physics

Physics

Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...

, a particle's distribution function is a function of seven variables, 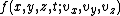, which gives the number of particles per unit volume in phase space

Phase space

In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...

. It is the number of particles per unit volume having approximately the velocity

Velocity

In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...

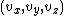  near the place 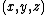and time 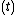. The usual normalization of the distribution function is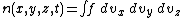



Here, N is the total number of particles and n is the number density of particles - the number of particles per unit volume, or the density

Density

The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...

 divided by the mass of individual particles.

A distribution function may be specialised with respect to a particular set of dimensions. E.g. take the quantum mechanical six dimensional phase space, 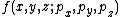and multiply by the total space volume, to give the momentum distribution i.e. the number of particles in the momentum phase space having approximately the momentum

Momentum

In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...

 .

Particle distribution functions are often used in plasma physics to describe wave-particle interactions and velocity-space instabilities. Distribution functions are also used in fluid mechanics

Fluid mechanics

Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...

, statistical mechanics

Statistical mechanics

Statistical mechanics or statistical thermodynamicsThe terms statistical mechanics and statistical thermodynamics are used interchangeably...

 and nuclear physics

Nuclear physics

Nuclear physics is the field of physics that studies the building blocks and interactions of atomic nuclei. The most commonly known applications of nuclear physics are nuclear power generation and nuclear weapons technology, but the research has provided application in many fields, including those...

.

The basic distribution function uses the Boltzmann constant 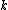 and temperature 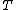with the number density to modify the normal distribution: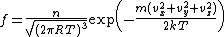


Related distribution functions may allow bulk fluid flow, in which case the velocity origin is shifted, so that the exponent's numerator is 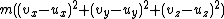; 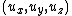is the bulk velocity of the fluid. Distribution functions may also feature non-isotropic temperatures, in which each term in the exponent is divided by a different temperature.

Plasma theories such as magnetohydrodynamics

Magnetohydrodynamics

Magnetohydrodynamics is an academic discipline which studies the dynamics of electrically conducting fluids. Examples of such fluids include plasmas, liquid metals, and salt water or electrolytes...

 may assume the particles to be in thermodynamic equilibrium

Thermodynamic equilibrium

In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...

. In this case, the distribution function is Maxwellian

Maxwellian

* Maxwell's equations * Maxwell–Boltzmann distribution* Maxwell's electromagnetic wave equation...

. This distribution function allows fluid flow and different temperatures in the directions parallel to, and perpendicular to, the local magnetic field. More complex distribution functions may also be used since plasmas

Plasma (physics)

In physics and chemistry, plasma is a state of matter similar to gas in which a certain portion of the particles are ionized. Heating a gas may ionize its molecules or atoms , thus turning it into a plasma, which contains charged particles: positive ions and negative electrons or ions...

 are rarely in thermal equilibrium.

The mathematical analog of a distribution is a measure

Measure (mathematics)

In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...

; the time evolution of a measure on a phase space is the topic of study in dynamical systems.